Dvě pružinky

Úloha číslo: 893

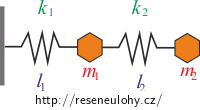
Na pružince klidové délky l₁ a tuhosti k₁ je připevněno závaží hmotnosti m₁. Na něm je na další pružince klidové délky l₂ a tuhosti k₂ upevněno závaží o hmotnosti m₂ (viz obrázek).

A) Napište lagrangián této soustavy. Neuvažujeme působení jiných sil než sil pružnosti obou pružinek.

B) Sestavte a vyřešte Lagrangeovy rovnice II. druhu pro případ rovnosti tuhostí obou pružin a hmotností obou závaží.

Nápověda 1A
Kolik má systém stupňů volnosti a kolik tedy budeme potřebovat zobecněných souřadnic?
Řešení nápovědy 1A
Soustava má dva stupně volnosti – každé závaží má jeden. Budeme tedy potřebovat dvě zobecněné souřadnice. Ideální je zvolit souřadnice tak, aby v nich bylo jednoduché vyjádřit kinetickou a potenciální energii, přičemž se ale může stát, že pro vyjádření každé energie jsou výhodnější jiné souřadnice. V takovém případě lze vyjádřit energie v různých souřadnicích a potom použít transformační vztahy mezi nimi.
Nápověda 2A
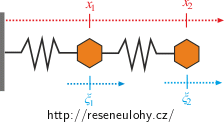
Označme jako souřadnice x₁, x₂ jsou souřadnicemi těžišť závaží měřených od místa pevného úchytu první pružiny. Jako souřadnice ξ₁, ξ₂ označíme změny délek pružinek oproti jejich klidové délce. Napište mezi nimi transformační vztahy.
Řešení nápovědy 2A
Transformační vztahy jsou:
\[x_1 = l_1 + \xi_1\ ,\] \[x_2 = l_1 + l_2 + \xi_1 + \xi_2\ ,\]
resp. obrácená transformace:
\[\xi_1 = x_1 -l_1\ ,\] \[\xi_2 = x_2 - \xi_1 - l_1 - l_2 = x_2 - x_1 - l_2\ .\]
Nápověda 3A
Kinetická energie se bude dobře vyjadřovat v souřadnicích měřených od pevného ukotvení první pružiny x₁, x₂. Napište její předpis a transformujte ho do souřadnic ξ₁, ξ₂.
Řešení nápovědy 3A
V soustavě x₁, x₂ se kinetická energie vyjádří snadno:
\[T(x_1, x_2) = \frac{1}{2}m_1\dot{x_1}^2+\frac{1}{2}m_2\dot{x_2}^2\ .\]
Potřebujeme tedy transformaci zobecněných rychlostí mezi souřadnicemi x₁, x₂ a ξ₁, ξ₂. Z časové derivace transformačních vztahů dostáváme:
\[\dot{x}_1 = \dot{\xi}_1\ ,\] \[\dot{x}_2 = \dot{\xi}_1+\dot{\xi}_1\ .\]
Odtud po dosazení do předpisu pro kinetickou energii v souřadnicích x₁, x₂ dostáváme:
\[T (\xi_1, \xi_2) = \frac{1}{2}m_1\dot{\xi_1}^2+\frac{1}{2}m_2(\dot\xi_1 + \dot\xi_2)^2 = \frac{1}{2}(m_1 + m_2)\dot{\xi_1}^2 + \frac{1}{2}m_2\dot{\xi_2}^2 + m_2\dot{\xi_1}\dot{\xi_2}\ .\]
Komentář – výpočet kinetické energie
Je vidět, že by bylo chybné napsat kinetickou energii pouze jako:
\[T = \frac{1}{2}m_1\dot{\xi}_1^2+\frac{1}{2}m_2\dot{\xi}_2^2\ .\]
Rychlost druhého závaží je totiž dána součtem \(\dot{\xi}_1\) a \(\dot{\xi}_2\). Součet je navíc v kvadrátu, takže vznikne i křížový člen s oběma proměnnými.
Nápověda 4A
Připomeňte si vzorec pro potenciální energii pružiny. Ve vhodných souřadnicích je možné zapsat potenciální energii soustavy velice jednoduše.
Řešení nápovědy 4A
Pro potenciální energii pružiny, která je ze své rovnovážné polohy vychýlena o vzdálenost Δl platí:
\[V = \frac{1}{2}k\Delta l^2\ .\]
Vzhledem k tomu, že máme dispozici souřadnice přímo určující prodloužení či zkrácení pružin oproti rovnovážnému stavu, není nic jednoduššího, než pro systém dvou pružinek psát:
\[V(\xi_1, \xi_2) = \frac{1}{2}k_1\xi_1^2 + \frac{1}{2}k_2\xi_2^2\ .\]
Odtud lagrangián ve zobecněných souřadnicích ξ₁, ξ₂:
\[L(\xi_1, \xi_2) = T(\xi_1, \xi_2)-V(\xi_1, \xi_2) = \frac{1}{2}(m_1 + m_2)\dot{\xi_1}^2 + \frac{1}{2}m_2\dot{\xi_2}^2 + m_2\dot{\xi_1}\dot{\xi_2} - \frac{1}{2}k_1\xi_1^2 - \frac{1}{2}k_2\xi_2^2 .\]
Samozřejmě by bylo možné lagrangián transformovat do souřadnic x₁, x₂, ale s tímto tvarem se nám bude pracovat o něco lépe.
Řešení A
Soustava má dva stupně volnosti – za každé závaží jeden. Zavedeme souřadnice x₁, x₂ (souřadnice těžišť závaží měřené od pevného ukotvení a orientovaného viz obrázek) a souřadnice ξ₁, ξ₂ (změny délek pružinek oproti jejich klidové délce).

Mezi souřadnicemi platí vztahy:
\[x_1 = l_1 + \xi_1\ ,\] \[x_2 = l_1 + l_2 + \xi_1 + \xi_2\ .\]
Kinetickou energii snadno vyjádříme v souřadnicích x₁, x₂:
\[T(x_1, x_2) = \frac{1}{2}m_1\dot{x_1}^2+\frac{1}{2}m_2\dot{x_2}^2\ .\]
Pomocí transformací zobecněných rychlostí:
\[\dot{x}_1 = \dot{\xi_1}\ ,\] \[\dot{x}_2 = \dot{\xi_1} + \dot{\xi_2}\ ,\]
pak můžeme kinetickou energii napsat pomocí souřadnic ξ₁, ξ₂:
\[T (\xi_1, \xi_2) = \frac{1}{2}m_1\dot{\xi_1}^2+\frac{1}{2}m_2(\dot\xi_1 + \dot\xi_2)^2 = \frac{1}{2}(m_1 + m_2)\dot{\xi_1}^2 + \frac{1}{2}m_2\dot{\xi_2}^2 + m_2\dot{\xi_1}\dot{\xi_2}\ .\]
Potenciální energii soustavy snadno napíšeme pomocí změn délek pružinek ξ₁, ξ₂:
\[V(\xi_1, \xi_2) = \frac{1}{2}k_1\xi_1^2 + \frac{1}{2}k_2\xi_2^2\ .\]
Odtud lagrangián:
\[L(\xi_1, \xi_2) = T(\xi_1, \xi_2)-V(\xi_1, \xi_2) = \frac{1}{2}(m_1 + m_2)\dot{\xi_1}^2 + \frac{1}{2}m_2\dot{\xi_2}^2 + m_2\dot{\xi_1}\dot{\xi_2} - \frac{1}{2}k_1\xi_1^2 - \frac{1}{2}k_2\xi_2^2\ .\]
Nápověda 1B
Lagrangeovy rovnice II. druhu mají tvar:

\[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial L}{\partial \dot{q}_{j}}\right)-\frac{\partial L}{\partial {q}_{j}} = 0\ ,\] pro j = 1, 2 ... n,

kde q_j je j-tá zobecněná souřadnice hmotného bodu a L Lagrangeova funkce.

V našem případě budeme mít dvě rovnice, protože soustava má dva stupně volnosti. Nezapomeňte, že rovnice máme sestavit a řešit pro zjednodušený případ (viz zadání).
Řešení – Soustava Lagrangeových rovnic II. druhu
Vzhledem ke zjednodušujícím podmínkám v zadání budeme vycházet z lagrangiánu ve tvaru:
\[L = m\dot{\xi_1}^2 + \frac{1}{2}m\dot{\xi_2}^2 + m\dot{\xi_1}\dot{\xi_2} - \frac{1}{2}k(\xi_1^2 + \xi_2^2)\ .\]
Nejprve ho zderivujeme tak, abychom si připravili derivace podle předpisu Lagrangeových rovnic II. druhu:
\[\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial L}{\partial \dot{\xi_1}} = \frac{\mathrm{d}}{\mathrm{d}t}(2m\dot{\xi}_1 + m\dot{\xi}_2) = 2m\ddot{\xi}_1 + m\ddot{\xi}_2\] \[\frac{\partial L}{\partial \xi_1} = -k\xi_1\] \[\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial L}{\partial \dot{\xi_2}} = \frac{\mathrm{d}}{\mathrm{d}t}(m\dot{\xi}_2+m\dot{\xi}_1) = m\ddot{\xi}_2+m\ddot{\xi}_1\] \[\frac{\partial L}{\partial \xi_2} = -k\xi_2.\]
Potom sestavíme soustavu Lagrangeových rovnic:
\[2\ddot{\xi}_1 + \ddot{\xi}_2 + \frac{k}{m}\xi_1 = 0\tag{1}\] \[\ddot{\xi}_1 + \ddot{\xi}_2 + \frac{k}{m}\xi_2 = 0\ ,\]
kterou máme vyřešit. Jedná se o homogenní soustavu dvou lineárních diferenciálních rovnic 2. řádu s konstantními koeficienty.
Nápověda 2B
Protože se jedná o homogenní soustavu dvou lineárních diferenciálních rovnic 2. řádu s konstantními koeficienty, zkusme předpokládat řešení ve tvaru:
\[\xi_1 = A_1 e^{i\omega t}\] \[\xi_2 = A_2 e^{i\omega t}\ ,\]
kde A₁, A₂ jsou obecně komplexní konstanty.

Fyzikálnějším argumentem pro tento tvar řešení je skutečnost, že očekáváme, že závaží budou na pružinách kmitat. To, co „zkoušíme“ předpokládat je fakt, že kmitají se stejnou úhlovou frekvencí ω.

Dosaďte předpokládaná řešení do soustavy Lagrangeových rovnic a získanou soustavu rovnic řešte.
Řešení B – mody kmitání
Dosadíme předpokládaný tvar řešení:
\[\xi_1 = A_1 e^{i\omega t}\] \[\xi_2 = A_2 e^{i\omega t}\]
do soustavy Lagrangeových rovnic a po úpravě dostáváme:
\[-2\omega^2A_1-\omega^2A_2 + \frac{k}{m}A_1=0\tag{2}\] \[-\omega^2A_1-\omega^2A_2 + \frac{k}{m}A_2=0\ .\]
V maticovém zápisu:
\[\left( \begin{matrix} -2\omega^2 + \frac{k}{m} & -\omega^2 \\ -\omega^2 & -\omega^2 + \frac{k}{m} \end{matrix} \right) \left( \begin{matrix} A_1\\ A_2 \end{matrix} \right) =0 \ .\]
Na tuto soustavu rovnic se lze dívat jako na podmínky svazující velikost amplitud kmitů obou pružinek a na úhlovou frekvenci ω jako na parametr. Jedná se o homogenní soustavu lineárních rovnic, proto bude mít netriviální řešení pouze v případě:
\[\det\left( \begin{matrix} -2\omega^2 + \frac{k}{m} & -\omega^2 \\ -\omega^2 & -\omega^2 + \frac{k}{m} \end{matrix} \right)=0\ .\]
Tedy:
\[\left(-2\omega^2 + \frac{k}{m}\right)\left(-\omega^2 + \frac{k}{m}\right)-\omega^4=0\ ,\] \[\omega^4 -3\frac{k}{m}\omega^2 + \left(\frac{k}{m}\right)^2=0\ .\]
Toto je rovnice čtvrtého řádu, která bude mít čtyři řešení. Pokud by se jednalo o obecnou rovnici čtvrtého řádu, byla by dosti obtížně řešitelná. Můžeme si ale všimnout, že se na ni můžeme dívat také jako na kvadratickou rovnici s neznámou ω² (tzv. bikvadratickou rovnici). Dostaneme kořeny:
\[\omega_{1{,}2}^{2} = \frac{3 \pm \sqrt{5}}{2}\frac{k}{m}\]
Parametr ω má fyzikální význam úhlové frekvence, takže musí být reálný a kladný. Dostáváme tedy pouze dvě fyzikálně přípustná řešení – dva mody kmitání:
\[\omega_1 = \sqrt{\frac{3+\sqrt{5}}{2}}\sqrt{\frac{k}{m}}\ ,\] \[\omega_2 = \sqrt{\frac{3-\sqrt{5}}{2}}\sqrt{\frac{k}{m}}\ .\]
Teď ještě zbývá najít vztah mezi amplitudami kmitání obou závaží, protože nejsou na sobě nezávislé. Svazující podmínku budeme hledat pro každý mód kmitání zvlášť prostým dosazením konkrétní hodnoty úhlové frekvence ω² do soustavy rovnic (2).
Komentář – triviální řešení
Samozřejmě, fyzikální smysl by mělo i triviální řešení soustavy rovnic – obě závaží by byla v klidu. Nás ale víc zajímá řešení popisující pohyb obou závaží.
Řešení B – svazující podmínky
Máme soustavu rovnic:
\[-2\omega^2A_1-\omega^2A_2 + \frac{k}{m}A_1=0\] \[-\omega^2A_1-\omega^2A_2 + \frac{k}{m}A_2=0\]
a dvě hodnoty parametru (resp. fyzikálně řečeno: úhlové frekvence) ω, pro které má tato soustava řešení:
\[\omega_1 = \sqrt{\frac{3+\sqrt{5}}{2}}\sqrt{\frac{k}{m}}\ ,\] \[\omega_2 = \sqrt{\frac{3-\sqrt{5}}{2}}\sqrt{\frac{k}{m}}\ .\]
Pro amplitudu kmitání m-tého závaží v n-tém modu zavedeme značení A_mn.

Hledejme nejdříve podmínku svazjící amplitudy pro první hodnotu úhlové frekvence (první mod):
\[\omega_1 = \sqrt{\frac{3+\sqrt{5}}{2}}\sqrt{\frac{k}{m}}\ .\]
Dosadíme do soustavy rovnic:
\[\left( \begin{matrix} -2 \frac{3+\sqrt{5}}{2}\frac{k}{m} + \frac{k}{m} & -\frac{3+\sqrt{5}}{2}\frac{k}{m} \\ -\frac{3+\sqrt{5}}{2}\frac{k}{m} & -\frac{3+\sqrt{5}}{2}\frac{k}{m} + \frac{k}{m} \end{matrix} \right) \left( \begin{matrix} A_{11}\\ A_{21} \end{matrix} \right) =0 \ .\]
Po úpravě:
\[\left( \begin{matrix} 4 + 2\sqrt{5} & 3+\sqrt{5} \\ 3+\sqrt{5} & 1+\sqrt{5} \end{matrix} \right) \left( \begin{matrix} A_{11}\\ A_{21} \end{matrix} \right) =0 \ .\]
Z první rovnice dostáváme:
\[(4 + 2\sqrt{5})A_{11} + (3 + \sqrt{5})A_{21} = 0\ .\]
Po úpravě a usměrnění zlomku dostáváme podmínku svazující amplitudy:
\[A_{21} = -\frac{1+\sqrt{5}}{2}A_{11}\ .\]
Analogicky dostaneme podmínku:
\[A_{22} = \frac{\sqrt{5}-1}{2}A_{12}\ .\]
V prvním modu tedy závaží kmitají v protifázi (amplitudy mají opačná znaménka), ve druhém ve fázi (amplitudy mají shodná znaménka).

Rovnice (1) jsou lineární, takže obecné řešení je dáno součtem řešení pro jednotlivé mody:
\[\xi_1(t) = A_{11}e^{i\sqrt{\frac{3+\sqrt{5}}{2}}\sqrt{\frac{k}{m}}t} + A_{12}e^{i\sqrt{\frac{3-\sqrt{5}}{2}}\sqrt{\frac{k}{m}}t}\] \[\xi_2(t) = -\frac{1+\sqrt{5}}{2}A_{11}e^{i\sqrt{\frac{3+\sqrt{5}}{2}}\sqrt{\frac{k}{m}}t}+\frac{\sqrt{5}-1}{2}A_{12}e^{i\sqrt{\frac{3-\sqrt{5}}{2}}\sqrt{\frac{k}{m}}t}\ .\]
Odpověď
Lagrangián soustavy dvou závaží na pružinkách popsané v zadání je:
\[L = \frac{1}{2}(m_1 + m_2)\dot{\xi_1}^2 + \frac{1}{2}m_2\dot{\xi_2}^2 + m_2\dot{\xi_1}\dot{\xi_2} - \frac{1}{2}k_1\xi_1^2 - \frac{1}{2}k_2\xi_2^2\ ,\]
kde ξ₁, ξ₂ jsou změny délek pružinek oproti jejich klidové délce.

Řešením Lagrangeových rovnic II. druhu pro případ rovnosti tuhostí obou pružin a hmotností obou závaží dostáváme:
\[\xi_1(t) = B_{11}\sin \left(\sqrt{\frac{3+\sqrt{5}}{2}}\sqrt{\frac{k}{m}}t+\varphi_{1}\right)+ B_{12}\sin\left( \sqrt{\frac{3-\sqrt{5}}{2}}\sqrt{\frac{k}{m}}t +\varphi_{2}\right)\] \[\xi_2(t) = -\frac{1+\sqrt{5}}{2}B_{11}\sin \left(\sqrt{\frac{3+\sqrt{5}}{2}}\sqrt{\frac{k}{m}}t+\varphi_{1}\right)+\frac{\sqrt{5}-1}{2}B_{12}\sin\left( \sqrt{\frac{3-\sqrt{5}}{2}}\sqrt{\frac{k}{m}}t +\varphi_{2}\right)\ ,\]
kde B₁₁, B₁₂ jsou konstanty o fyzikálním významu amplitud kmitání prvního závaží v jednotlivých modech a φ_n jsou počáteční fáze v n-tém modu.