Tenzor setrvačnosti tyče
Úloha číslo: 2235
Určete složky tenzoru setrvačnosti velmi tenké homogenní tyče délky \(l\) vzhledem k jejímu hmotnému středu a určete moment setrvačnosti této tyče vzhledem k ose procházející hmotným středem a určené vektorem \(\vec {n} = \left ( \, \frac {\sqrt 2}{2}; \, 0 ; \,\frac {\sqrt 2}{2} \right ) \).
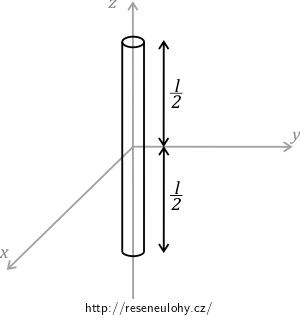
Nápověda 1
Rozvažte, jakých vztahů budete užívat a jaké všechny veličiny k tomu budete potřebovat.
Nápověda 2
Určujte postupně jednotlivé složky tenzoru a zapište je do matice.
Rozmyslete si, jak bude v našem případě vypadat daný objemový integrál a určete integrační meze.
Nápověda 3
Rozmyslete si, jaký vztah platí pro moment setrvačnosti vůči ose zadané směrovým vektorem \(\vec {n} = \left ( \, \frac {\sqrt 2}{2}; \, 0 ; \,\frac {\sqrt 2}{2} \right ) \).
Celkové řešení
Pro určení jednotlivých složek tenzoru setrvačnosti \(J_{jk}\) spojitého prostředí platí vztah:
\[J_{jk}= \int_V^{}{( \delta_{jk} \, r^2 - x_j \, x_k ) \rho} \, \mathrm{d}V,\tag{2}\]kde \(r\) je vzdálenost od počátku soustavy, \(\delta_{jk}\) je Kroneckerovo delta a souřadnice polohového vektoru \(x_i\) pro \(i=\) 1 až 3 jsou obecnějším zapsáním našich souřadnic \(x, \, y, \, z\).
Potřebujeme znát také hustotu tyče \(\rho\). Naše tyč je homogenní, proto je hustota \(\rho\) konstantní.
Určeme nejprve složku \(J_{xx}\) tenzoru setrvačnosti tyče podle vztahu (2):
\[J_{xx}=J_{11}= \int_{V} {( \delta_{11} \, r^2 - x_1 \, x_1 ) \rho} \, \mathrm{d}V = \int_{V} {(\,y^2 + z^2) \rho} \, \mathrm{d}V.\]Tyč je velmi tenká, a proto bude snazší uvažovat lineární hustotu \(\eta\) namísto objemové \(\rho\). Náš integrál se zjednoduší na prostý integrál proměnné \(z\). Tenzor určujeme vzhledem k hmotnému středu tyče, tudíž integrační meze budou odpovídat polovině délky tyče a budeme integrovat od \(- \frac {l}{2}\) do \(\frac {l}{2}\). Tyto úvahy vedou ke vztahu:
\[J_{xx}=\eta \, \int_{- \frac {l}{2}}^{\frac {l}{2}} {(\,y^2 + z^2)} \, \mathrm{d}z = \eta \left [ zy^2 + \frac {z^3}{3} \right ] _{\,\, - \frac {l}{2}}^{\frac {l}{2}}.\]Ovšem \(y\) souřadnice tyče je nulová, proto dále platí:
\[J_{xx}=\frac {1}{3} \eta \left [ z^3 \right ] _{\,\, - \frac {l}{2}}^{\frac {l}{2}}=\frac {1}{3} \eta \left ( \frac {l^3}{8} + \frac {l^3}{8} \right ) = \frac {1}{12} l^2 \left ( \eta \, l \right ).\]Vztah \(\eta \, l\) vyjadřuje celkovou hmotnost tyče. Tuto hmotnost označme \(m\). Tedy pro složku \(J_{xx}\) dostaneme:
\[J_{xx}= \frac {1}{12} ml^2.\]Další postupy zestručníme, jsou totiž velmi podobné postupu předešlému.
Dále určeme složku \(J_{yy}\):
\[J_{yy}= \int_{V} {( \delta_{22} \, r^2 - y^2 ) \rho} \, \mathrm{d}V = \int_{- \frac {l}{2}}^{\frac {l}{2}} {( \, x^2 + z^2 ) \eta} \, \mathrm{d}z = \eta \left [ zx^2 + \frac {z^3}{3} \right ] _{\,\, - \frac {l}{2}}^{\frac {l}{2}}.\]Pro naši tyč platí, že \(x=0\), a dále:
\[J_{yy}= \frac {1}{12} l^2 \left ( \eta \, l \right ) = \frac {1}{12} ml^2.\]Přesuňme se ke složce \(J_{zz}\).
\[J_{zz}= \int_{V} {( \delta_{33} \, r^2 - z^2 ) \rho} \, \mathrm{d}V = \int_{- \frac {l}{2}}^{\frac {l}{2}} {( \, x^2 + y^2 ) \eta} \, \mathrm{d}z = \eta \left [ zx^2 + zy^2 \right ] _{\,\, - \frac {l}{2}}^{\frac {l}{2}} = 0\] \[J_{zz} = 0\]Složky odpovídající momentům setrvačnosti vzhledem k rotaci okolo příslušných os bychom měli, dále se věnujme deviačním momentům. Pro \(J_{xy}\) platí:
\[J_{xy}= \int_{V} {( \delta_{12} \, r^2 - xy ) \rho} \, \mathrm{d}V = \int_{- \frac {l}{2}}^{\frac {l}{2}} {( \, -xy ) \eta} \, \mathrm{d}z = 0 \]Cyklickou záměnou zjistíme, že ve vztahu pro libovolný deviační moment se vždy vyskytuje \(x\) nebo \(y\), které jsou nulové. Všechny deviační momenty proto budou nulové:
\[J_{xy}=J_{yz}=J_{xz}=0.\]Zapíšeme tenzor setrvačnosti naší tyče v podobě matice:
\[J_{ij} = \begin{pmatrix} \frac {1}{12} ml^2 & 0 & 0\\ 0 & \frac {1}{12} ml^2 & 0\\ 0 & 0 & 0 \end{pmatrix} .\]Pro moment setrvačnosti \(J_\vec \nu\) tyče vzhledem k ose zadané jednotkovým vektorem \(\vec \nu\) platí:
\[J_\vec \nu = J_{ij} \nu_i \nu_j .\tag{3}\]Prostým výpočtem ověřme, že náš vektor \(\vec {n} = \left ( \, \frac {\sqrt 2}{2}; \, 0 ; \,\frac {\sqrt 2}{2} \right ) \) je jednotkový.
\[\left \| \vec {n} \right \| = \sqrt {\left ( \frac {\sqrt 2}{2} \right )^2 + \left ( \frac {\sqrt 2}{2} \right )^2} = \sqrt {\frac {1}{2} + \frac {1}{2}} = \sqrt 1 = 1 .\]Je třeba si uvědomit, že ve vztahu (3) jsou použity dvě Einsteinovy sumační konvence, tedy po dosazení \(\vec n\) získáme:
\[J_\vec n = \sum_{i=1}^{3} \, \sum_{j=1}^{3} \, J_{ij} n_i n_j =\] \[\,\,\,\, = J_{xx} n_x n_x + J_{xy} n_x n_y + J_{xz} n_x n_z +\] \[\,\,\,\, + J_{yx} n_y n_x + J_{yy} n_y n_y + J_{yz} n_y n_z +\] \[\,\,\,\, + J_{zx} n_z n_x + J_{zy} n_z n_y + J_{zz} n_z n_z =\] \[= \frac {1}{12} ml^2 \frac {\sqrt 2}{2} \frac {\sqrt 2}{2} = \frac {ml^2}{24}.\]Moment setrvačnosti \(J_\vec n\) naší tyče vůči ose dané vektorem \(\vec n\) je \(\frac {ml^2}{24}\).
Odpověď
Námi hledaný tenzor setrvačnosti velmi tenké homogenní tyče vůči počátku soustavy souřadnic má tvar:
\[J_{ij}= \begin{pmatrix} \frac {1}{12} ml^2 & 0 & 0\\ 0 & \frac {1}{12} ml^2 & 0\\ 0 & 0 & 0 \end{pmatrix} .\]Moment setrvačnosti této tyče vůči ose dané směrem \(\vec {n} = \left ( \, \frac {\sqrt 2}{2}; \, 0 ; \,\frac {\sqrt 2}{2} \right ) \) je:
\[J_\vec n = \frac {ml^2}{24}.\]


