Matematické kyvadlo – rovnovážné polohy

Úloha číslo: 919

Nalezněte rovnovážné polohy matematického kyvadla hmotnosti m a délky l v homogenním gravitačním poli o tíhovém zrychlení g pomocí zobecněného principu virtuální práce.

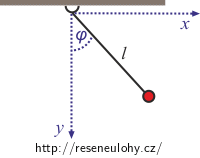
Počátek kartézské soustavy souřadnic umístíme do úchytu kyvadla. Vyřešte úlohu pro případ, že si za parametr určující polohu kyvadla vezmeme jeho okamžitou výchylku φ, i pro případ, že úlohu budeme řešit v kartézských souřadnicích x, y.

Poznámka: Obvykle definujeme matematické kyvadlo jako hmotný bod na nehmotném vlákně. Pro výpočty však neuvažujeme, že by se vlákno mohlo ohýbat. Spíše si tedy představujme „hmotný bod na nehmotné tyčce“

Nápověda 1
Napište podmínky, které musí pohyb kyvadla splňovat vzhledem k parametru φ a v kartézských souřadnicích.

Stačí si vzpomenout na parametrickou a středovou rovnici kružnice.
Řešení nápovědy 1
Vzhledem k parametru φ platí:
\[x(\varphi) = l\sin \varphi,\tag{1}\] \[y(\varphi) = l\cos \varphi.\]
Kyvadlo se pohybuje po kružnici. Z Pythagorovy věty tedy musí platit:
\[x^2 + y^2 = l^2.\tag{2}\]
Tento vztah charakterizuje vazebnou podmínku.
Nápověda 2
Jaké síly na kyvadlo působí? Které jsou vazebné a které aktivní?
Řešení nápovědy 2
Na kyvadlo působí gravitační síla:
\[\vec{F}_g = (0,\ mg)\]
a tahová síla provázku. Ta je ovšem silou vazebnou, takže jí vykonaná virtuální práce bude vždy nulová.

Působí tedy jediná aktivní síla, a to pouze ve směru kartézské osy y. Můžeme psát:
\[F_y = mg.\]
Nápověda 3
Nyní bychom potřebovali určit vektor virtuálních, infinitezimálně malých posunutí slučitelných s vazbami. Budeme ho ale potřebovat „celý“? Nestačila by nám jen jedna složka?
Řešení nápovědy 3
Zobecněný princip virtuální práce lze zapsat vztahem:
\[\sum_{i=1}^{N} \vec{F}_i \cdot \delta \vec{r}_i = 0\ .\]
Jedná se tedy o sumu skalárních součinů všech aktivních sil působících na systém N částic s jejich vratnými, virtuálními, infinitezimálně malými posunutími slučitelnými s vazbami je nulová. \(\vec{F}_i\) je výslednice sil působící na i-tou částici, \(\delta \vec{r}_i\) je vektor nekonečně malého posunutí slučitelného s vazbami i-té částice.

Pro jednu částici v dvoudimenzionálních kartézských souřadnicích můžeme psát:
\[(F_x, F_y) \cdot (\mathrm{d}x, \mathrm{d}y) = 0,\]
kde F_x, F_y jsou složky výslednice aktivních sil.

V našem případě tedy dostáváme:
\[(0, mg) \cdot (\mathrm{d}x, \mathrm{d}y) = 0.\]
Stačí nám proto pracovat s rovnicí:
\[mg\, \mathrm{d}y = 0.\tag{3}\]
Nápověda 4
Napište vztah pro virtuální, vratné, infinitezimálně malé posunutí dy slučitelné s vazbami danými rovnicemi (1) a (2).
Řešení nápovědy 4
Parametrizujeme-li podle výchylky φ dostáváme jednoduše:
\[y(\varphi) = l\cos \varphi,\] \[\mathrm{d}y = -l\sin \varphi\,\mathrm{d}\varphi.\]
O něco složitější bude vyjádření z vazebné podmínky (2) pro kartézské souřadnice. Pokud platí:
\[x^2 + y^2 = l^2,\tag{2}\]
pak diferencováním rovnice dostaneme:
\[2x\, \mathrm{d}x + 2y\, \mathrm{d}y = 0\]
a po úpravě:
\[\mathrm{d}y = -\frac{x}{y}\,\mathrm{d}x.\]
Dosazením za x z (2) pak dostaneme:
\[\mathrm{d}y = \pm\frac{\sqrt{l^2-y^2}}{y}\mathrm{d}x.\]
Znaménko není jednoznačné, protože x není z vazebné podmínky (2) jednoznačně určeno.
Nápověda 5
Nyní stačí správně dosadit do vztahu (3). Ujistěte se, že rovnice získané na základě vazebných podmínek (1), (2) mají řešení o shodném fyzikálním významu.
Řešení nápovědy 5
Nejdříve vztah (1*), tedy parametrizace pomocí výchylky φ:
\[-mgl\sin \varphi\, \mathrm{d}\varphi = 0.\]
Vykrátíme konstanty a dostáváme rovnici:
\[\sin \varphi = 0,\]
která má dvě řešení:
\[\varphi_1 = 0,\] \[\varphi_2 = \pi.\]
(Další, o periody posunutá řešení mají stále stejný fyzikální význam.)

Teď se věnujme vazebné podmínce (2):
\[\pm mg\frac{\sqrt{l^2-y^2}}{y}\mathrm{d}x = 0.\]
Vykrátíme konstanty:
\[\frac{\sqrt{l^2-y^2}}{y} = 0\]
a dostáváme rovnici v podílovém tvaru, jejíž řešení se omezuje na řešení rovnice:
\[l^2-y^2 = 0,\]
jejíž kořeny jsou:
\[y_1 = l,\] \[y_2 = -l.\]
(Ani jedno řešení není nula, neznámá ve jmenovateli tedy nevadí).

Můžeme snadno ověřit, že jde jen o dvě různým způsobem zapsané, ale geometricky shodné polohy. Rozmyslete si, o jaký typ rovnovážné polohy se jedná (stabilní, labilní, indiferentní)?
Řešení
Napíšeme rovnice polohy kyvadla vzhledem k možným parametrizacím.

Podle výchylky φ:
\[x(\varphi) = l\sin \varphi\tag{1}\] \[y(\varphi) = l\cos \varphi\]
a v kartézských souřadnicích:
\[x^2 + y^2 = l^2.\tag{2}\]
Vektor gravitační, jediné aktivní působící síly má nenulovou pouze svou vertikální složku
\[\vec{F}_g = (0, mg).\]
Zobecněný princip virtuální práce se nám tedy zredukuje na tvar:
\[F_y\,\mathrm{d}y = 0.\]
Diferencováním vztahů (1) resp. (2) dostáváme:
\[dy = -l\sin \varphi \,\mathrm{d}\varphi,\]
resp.
\[\mathrm{d}y = \pm\frac{\sqrt{l^2-y^2}}{y}\,\mathrm{d}x.\]
Dosazením dostáváme zobecněný princip virtuální práce ve tvarech:
\[-mgl\sin \varphi\, \mathrm{d}\varphi = 0,\] \[\pm mg\frac{\sqrt{l^2-y^2}}{y}\,\mathrm{d}x = 0.\]
Vzhledem k tomu, že se jedná o rovnice v součinovém tvaru, nejednoznačnost znaménka před celým výrazem v druhém vztahu řešení neovlivní.

Řešením těchto rovnic pro parametr φ, resp. y, dostáváme:

\[\varphi_1 = 0\,\,\] \[y_1 = l\]
\[\varphi_2 = \pi\,\,\] \[y_2 = -l.\]

Pro úplnost můžeme doplnit, že dosazením do vazebné podmínky (2) dostaneme:
\[x_1 = x_2 = 0.\]
Můžeme snadno ověřit, že jde jen o dvě různým způsobem zapsané, ale geometricky shodné polohy. Rozmyslete si, o jaký typ rovnovážné polohy se jedná (stabilní, labilní, indiferentní)?
Odpověď
Kyvadlo má dvě rovnovážné polohy. Ty mohou být popsány ekvivalentními podmínkami:

\(\varphi_1 = 0\) odpovídá \(y_1 = l \ \wedge \ x_1=0\ ,\)

\(\varphi_2 = \pi\) odpovídá \(y_2 = -l \ \wedge \ x_2=0.\)
Komentář – stabilní a labilní poloha
Kyvadlo má rovnovážné polohy v nejvyšším a nejnižším bodě, do kterého se může dostat (horní a dolní úvrati).

Jeho potenciální energie nabývá maxima v nejvyšším bodě – jedná se tedy o polohu labilní – a naopak nejnižší možnou potenciální energii má v nejnižším bodě své trajektorie – zde je tedy v poloze stabilní.
Komentář – kyvadlo na vlákně
Pokud bychom skutečně uvažovali, že závaží kyvadla je zavěšeno vlákně (které mu nedovolí vzdálit se do větší vzdálenosti od uchycení než l, ale umožní mu pohyb ve vzdálenostech menších), nikoli na nedeformovatelné tyčce, pak je jasné, že rovnovážnou polohu v nejvyšším bodě mít nemůže.

Závaží na tyčce se liší od závaží na vlákně matematickou formulací vazebné podmínky. Pro kyvadlo na nedeformovatelné tyčce je vazba oboustranná:
\[x^2 + y^2 = l^2,\]
zatímco pro kyvadlo na vlákně je pouze jednostranná:
\[x^2 + y^2 \leq l^2.\]
Řešení by v tomto případě bylo podstatně složitější, protože z podmínky mimo jiné vyplývá, že kyvadlo má dva stupně volnosti. Může se pohybovat nejen po obvodu kruhu, ale i v jeho vnitřní oblasti.