Hmotný bod na rovnoměrně se otáčející nakloněné rovině

Úloha číslo: 741

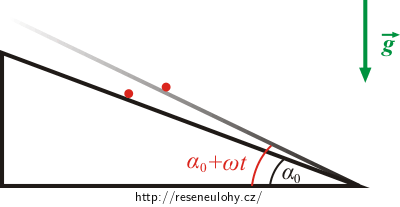
Hmotný bod o hmotnosti m se pohybuje bez tření po nakloněné rovině svírající s vodorovnou podložkou úhel α(t), gravitační zrychlení má směr kolmý na vodorovnou podložku a velikost g.

Hmotný bod se po nakloněné rovině pohybuje pouze nahoru nebo dolů (nemůže konat pohyb kolmý na nákresnu). Úlohu řešíme pouze pro velikosti úhlů od 0 do \(\frac{\pi}{2}\), tj. od vodorovné roviny po kolmou stěnu – volný pád.

Úhel nakloněné roviny α(t) závisí na čase předpisem:

\[\alpha\left(t\right)=\omega t + \alpha_0\ .\]

A) Určete Lagrangeovu funkci hmotného bodu a vyřešte pohybové rovnice.

B) Představte si, že by měly věžní hodiny 1 metr dlouhou vteřinovou ručičku. Vypočtěte, za jak dlouho by se hmotný bod umístěný na jejím konci dostal do středu ciferníku. Hmotný bod umístíme na konec vteřinové ručičky přesně v momentě, kdy je na devítce. Konečný číselný výpočet je potřeba provádět pomocí příslušného softwaru numericky. Konečná rovnice není analyticky řešitelná.

Nápověda 1
Projděte si nejprve úlohu Hmotný bod na nakloněné rovině. Je zřejmé, že úloha, kterou právě řešíme, je jejím přímým zobecněním a často budeme používat stejné postupy.
Nápověda 2
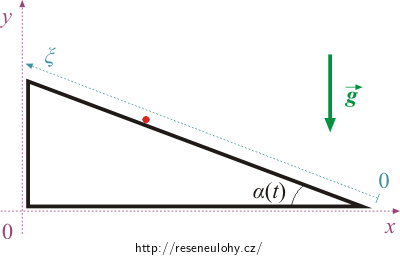
Souřadnice zvolíme stejně jako v úloze Hmotný bod na nakloněné rovině. Pouze ξ má opačnou orientaci. Vyjdou nám tak o něco jednodušší rovnice a snáze čitelné grafy. Úloha by ale samozřejmě byla řešitelná i s orientací ξ směrem po povrchu nakloněné roviny dolů.

Napište vztah mezi souřadnicemi x, y a ξ.
Řešení nápovědy 2
Můžeme vyjít z úlohy Hmotný bod na nakloněné rovině, nesmíme však opomenout časovou závislost sklonu roviny a opačnou orientaci ξ. Pro souřadnice x a y platí:
\[x = x_0 - \xi \cos (\alpha\left(t\right))\ ,\] \[y = \xi \sin (\alpha\left(t\right))\ ,\]
tj. po dosazení zadané časové závislosti sklonu nakloněné roviny:
\[x = x_0 - \xi \cos (\omega t+\alpha_0)\ ,\] \[y = \xi \sin (\omega t+\alpha_0)\ .\]
Nápověda 3
Vyjádřete složky rychlosti ve směru os x a y pomocí souřadnice ξ, spočtěte velikost rychlosti a napište vyjádření kinetické energie hmotného bodu vzhledem k souřadnici ξ.
Řešení nápovědy 3
Poloha hmotného bodu v kartézských souřadnicích je popsána takto:
\[x = x_0 - \xi \cos (\alpha\left(t\right))\] \[y = \xi \sin (\alpha\left(t\right))\ .\]
Složky rychlosti dostáváme derivováním podle času:
\[\dot{x} = -\dot{\xi}\cos (\omega t+\alpha_0) + \xi \omega \sin (\omega t+\alpha_0)\] \[\dot{y} = \dot{\xi}\sin (\omega t+\alpha_0) + \xi \omega \cos (\omega t+\alpha_0)\ .\]
Pro velikosti rychlostí platí:
\[|v(\xi)|^2=|\dot{x}|^2 + |\dot{y}|^2\ .\]
Dosadíme a upravíme:
\[|v(\xi)|^2 = \dot{\xi}^2[\cos^2 (\omega t+\alpha_0) + \sin^2 (\omega t+\alpha_0)] + \xi^2 \omega^2 [\sin^2 (\omega t+\alpha_0)+\cos^2 (\omega t+\alpha_0)]+\] \[+2\dot{\xi}\xi\omega\sin(\omega t + \alpha_0)\cos(\omega t + \alpha_0) - 2\dot{\xi}\xi\omega\sin(\omega t + \alpha_0)\cos(\omega t + \alpha_0) = \dot{\xi}^2+\xi^2\omega^2\ .\]
Z řešení je vidět, že vlastně skládáme rychlost podél nakloněné roviny s rychlostí pohybu po kružnici o poloměru ξ.

Pro kinetickou energii tedy dostáváme:
\[T = \frac{1}{2}m\dot{\xi}^2 + \frac{1}{2}m\xi^2\omega^2\ .\]
Nápověda 4
Je zřejmé, že i potenciální energii můžeme vyjádřit obdobně jako v úloze Hmotný bod na nakloněné rovině, ale musíme mít na zřeteli i časový průběh děje.
Řešení nápovědy 4
Pro potenciální energii dostáváme:
\[V = mg\xi\sin(\alpha\left(t\right))\ ,\]
resp.
\[V(\xi, t) = mg\xi\sin(\omega t+ \alpha_0)\ .\]
Potenciální energie je tedy závislá jak na zobecněné souřadnici, tak i na čase.
Řešení – lagrangián

Při popisu polohy hmotného bodu na nakloněné rovině vyjdeme z úlohy Hmotný bod na nakloněné rovině, pouze souřadnice ξ bude oriantována opačně:
\[x = x_0 - \xi \cos (\alpha\left(t\right))\ ,\] \[y = \xi \sin (\alpha(t))\ .\]
Složky rychlosti dostáváme derivováním podle času:
\[\dot{x} = -\dot{\xi}\cos (\omega t+\alpha_0) + \xi \omega \sin (\omega t+\alpha_0)\ ,\] \[\dot{y} = \dot{\xi}\sin (\omega t+\alpha_0) + \xi \omega \cos (\omega t+\alpha_0)\ .\]
Odtud pro velikost rychlosti:
\[|\dot{\xi}|^2=|\dot{x}|^2 + |\dot{y}|^2 = \dot{\xi}^2+\xi^2\omega^2\ .\]
Pro kinetickou energii tedy dostáváme:
\[T = \frac{1}{2}m\dot{\xi}^2 + \frac{1}{2}m\xi^2\omega^2\ .\]
Pro potenciální energii zjevně platí:
\[V = mg\xi\sin(\alpha\left(t\right)) = mg\xi\sin(\omega t+ \alpha_0)\ .\]
Lagrangeova funkce má tvar:
\[L = T - V\ .\]
Po dosazení energií:
\[L = \frac{1}{2}m\dot{\xi}^2 + \frac{1}{2}m\xi^2\omega^2 - mg\xi\sin(\omega t+ \alpha_0)\ .\]
Nápověda 5
Připomeneme si obecný vzorec pro určení Lagrangeových rovnic II. druhu pomocí Lagrangeovy funkce:

\[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial L}{\partial \dot{q}_{j}}\right)-\frac{\partial L}{\partial {q}_{j}} = 0\ ,\] pro j = 1, 2 ... n.

V našem případě máme jen jednu zobecněnou souřadnici, a proto budeme mít jednu Lagrangeovu rovnici.

Připravte si derivace Lagrangeovy funkce potřebné k sestavení Lagrangeovy rovnice. Ta je v našem případě závislá nejen na zobecněné souřadnici a zobecněné rychlosti, ale i na čase. Dávejte proto pozor zejména na pořadí derivací!
Řešení nápovědy 5
Nejprve derivace lagrangiánu podle zobecněné rychlosti:
\[\frac{\partial L}{\partial \dot{\xi}} = m\dot{\xi}\ .\]
Ačkoli je lagrangián explicitně závislý na čase, po derivaci podle zobecněné rychlosti tato závislost mizí. Můžeme tedy pak psát již velmi jednoduše:
\[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial L}{\partial \dot{\xi}}\right) = \frac{\mathrm{d}}{\mathrm{d}t}(m\dot{\xi}) = m\ddot{\xi}\ .\]
Nicméně všimněte si, jak je v tomto případě pořadí derivací důležité!

A potom derivace lagrangiánu podle zobecněné souřadnice:
\[\frac{\partial L}{\partial \xi} = m\xi\omega^2 - mg\sin(\omega t + \alpha_0)\ .\]
Dosazením do předpisu dostáváme Lagrangeovu rovnici:
\[m\ddot{\xi} - m\xi\omega^2 + mg\sin(\omega t + \alpha_0) = 0\]
a po úpravě:
\[\ddot{\xi}-\xi\omega^2=-g\sin(\omega t + \alpha_0)\ .\]
Nápověda 6
Dospěli jsme k diferenciální rovnici:
\[\ddot{\xi}-\xi\omega^2=-g\sin(\omega t + \alpha_0)\ .\]
Jedná se o lineární diferenciální rovnici 2. řádu s konstantními koeficienty a pravou stranou. Tu lze řešit metodou variace konstanty nebo přímo metodou speciální pravé strany.
Řešení nápovědy 6
V rychlosti projdeme kroky v řešení rovnice
\[\ddot{\xi}-\xi\omega^2=-g\sin(\omega t + \alpha_0)\ ,\]
Nejprve je třeba vyřešit homogenní rovnici (indexem H budeme označovat její řešení):
\[\ddot{\xi}_H-\xi_H\omega^2=0\] \[\xi_H = C_1e^{\omega t} + C_2e^{-\omega t}\]
a k němu přičíst partikulární řešení (pravá strana má speciální tvar, proto ho známe):
\[\xi = C_1e^{\omega t} + C_2e^{-\omega t} + K\sin(\omega t + \alpha_0)\ .\]
Dosazením do původní rovnice určíme konstantu K a tím získáme obecné řešení ve tvaru:
\[\xi = C_1e^{\omega t} + C_2e^{-\omega t} + \frac{g}{2\omega^2}\sin(\omega t + \alpha_0)\ ,\]
kde C₁ a C₂ jsou integrační konstanty, které je možné určit z počátečních podmínek.
Řešení – Lagrangeovy rovnice II. druhu
Dospěli jsme k lagrangiánu:
\[L = \frac{1}{2}m\dot{\xi}^2 + \frac{1}{2}m\xi^2\omega^2 - mg\xi\sin(\omega t+ \alpha_0)\ .\]
Příslušnými derivacemi a úpravou dostáváme Lagrangeovu rovnici:
\[\ddot{\xi}-\xi\omega^2=-g\sin(\omega t + \alpha_0)\ .\]
Jedná se o lineární diferenciální rovnici 2. řádu s konstantními koeficienty a pravou stranou. Jejím řešením (podrobněji v nápovědě) je funkce:
\[\xi = C_1e^{\omega t} + C_2e^{-\omega t} + \frac{g}{2\omega^2}\sin(\omega t + \alpha_0)\ ,\]
kde C₁ a C₂ jsou integrační konstanty, které je možné určit z počátečních podmínek.
Nápověda 7
Přeložte pokyny ze zadání do rovnice tak, abyste dopočítali konstanty v obecném řešení rovnice. Zejména se zaměřte na informace:
1. Hmotný bod se začíná pohybovat ve chvíli, kdy je ručička na devítce a nachází se v tu chvíli na jejím konci.
2. Hmotný bod je na začátku v klidu.
3. Ručička je vteřinová.
Interpretace
1. \(\alpha_0 = 0\), \(\ \xi(0)=1 \ \mathrm{m}\)
2. \(\dot{\xi}(0)=0 \ \mathrm{m\cdot s^{-1}}\)
3. \(\omega = \frac{\pi}{30} s^{-1} \approx 0{,}1 \ \mathrm{s^{-1}}\)
Výpočet integračních konstant
Z uvedených podmínek:
\[\xi(0)=1\] \[\dot{\xi}(0)=0\ ,\]
vyplývá soustava rovnic pro konstanty C₁ a C₂:
\[C_1+C_2 = 1\] \[\omega(C_1-C_2) + \frac{g}{2\omega}=0\ .\]
Jejím řešením je dvojice:
\[C_1 = \frac{2\omega^2-g}{4\omega^2}\] \[C_2 = \frac{2\omega^2+g}{4\omega^2}\ .\]
Dosazením za počáteční úhel a úhlovou rychlost dostáváme:
\[\xi(t) = -249{,}5e^{0{,}1t}+250{,}5e^{-0{,}1t} + 500\sin (0{,}1t)\ .\]
Správně by v tomto vztahu měly být složené závorky naznačující, že jde o číselné hodnoty. Pro zpřehlednění vztahu je nebudeme psát s tím, že všechny veličiny jsou uvedeny v základních jednotkách SI.
Řešení – rovnice pohybu po vteřinové ručičce
V předchozí části úlohy jsme dospěli k obecnému řešení rovnice popisující pohyb bodu po nakloněné rovině s proměnlivým úhlem sklonu:
\[\xi = C_1e^{\omega t} + C_2e^{-\omega t} + \frac{g}{2\omega^2}\sin(\omega t + \alpha_0)\ .\]
Informace, které jsou uvedeny v zadání, můžeme interpretovat jako počáteční podmínky pohybu hmotného bodu po vteřinové ručičce takto:
\[\xi(0)=1 \ \mathrm{m}\] \[\dot{\xi}(0)=0 \ \mathrm{m}\cdot \mathrm{s}^{-1}\] \[\alpha_0 = 0\] \[\omega \approx 0{,}1 \ \mathrm{s}^{-1}\ .\]
Z prvních dvou dopočítáme konstanty C₁ a C₂:
\[C_1 = \frac{2\omega^2-g}{4\omega^2}\] \[C_2 = \frac{2\omega^2+g}{4\omega^2}\ .\]
Dosazením do obecného řešení dostáváme rovnici:
\[\xi(t) = -249{,}5e^{0{,}1t}+250{,}5e^{-0{,}1t} + 500\sin (0{,}1t)\ .\]
Správně by v tomto vztahu měly být složené závorky naznačující, že jde o číselné hodnoty. Pro zpřehlednění vztahu je nebudeme psát s tím, že všechny veličiny jsou uvedeny v základních jednotkách SI.

Zbývá vyřešit, kdy hmotný bod dorazí do středu ciferníku, který je vzhledem k volbě zobecněné souřadnice v jejím počátku. Hledáme tedy, pro jaké t platí:
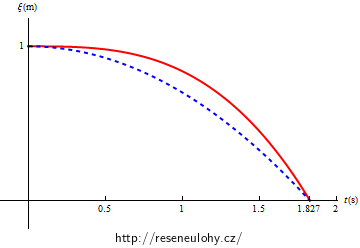
\[0 = -249{,}5e^{0{,}1t}+250{,}5e^{-0{,}1t} + 500\sin (0{,}1t)\ .\]
Rovnice je dost komplikovaná a analyticky neřešitelná. Můžete se pokusit ji vyřešit pomocí vhodného softwaru, například si můžete nechat nakreslit graf souřadnice ξ jako funkce času a odečíst hodnotu na časové ose:

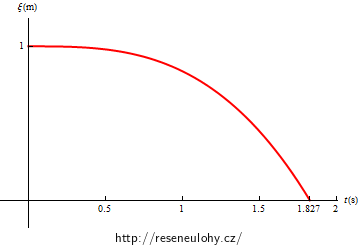
Z grafu je vidět, že hledané t se rovná přibližně 1,8 s.

Komentář
Z grafu je velmi pěkně vidět, že jsme konstanty v rovnici určili správně. Bod je na začátku pohybu v klidu a nějakou dobu ještě téměř nemění svoji pozici, protože jeho počáteční rychlost je nulová a vteřinová ručička je na začátku vodorovně (tj. zrychlení na úplném začátku je také nulové).

Ještě více je rozdíl oproti pohybu po nakloněné rovině s neměnným úhlem sklonu vidět, pokud si do stejného grafu nakreslíme pohyb hmotného bodu na nakloněné rovině s takovým sklonem, aby hmotný bod na ni položený urazil 1 m také za čas 1,8 s (grafem je parabola, na obrázku modře čárkovaně). To bychom například mohli „realizovat“ stejně dlouhou minutovou ručičkou ukazující chvíli po tři čtvrtě – nakloněná rovina musí mít sklon asi 3,5 stupně).

Rozdíl je dán zejména tím, že ačkoli se hmotné body v obou případech pohybují ze stejné vzdálenosti a se stejnou počáteční rychlostí, ten na minutové ručičce se pohybuje už od začátku s nenulovým zrychlením.
Odpověď
Pohybová rovnice hmotného bodu na nakloněné rovině s proměnným úhlem sklonu je:
\[\xi = C_1e^{\omega t} + C_2e^{-\omega t} + \frac{g}{2\omega^2}\sin(\omega t + \alpha_0)\ ,\]
kde C₁ a C₂ jsou integrační konstanty, které je možné určit z počátečních podmínek.

Hmotný bod umístěný na vteřinové ručičce věžních hodin se dokutálí do středu ciferníku přibližně za 1,8 s. Širší komentář tohoto výpočtu viz sekce výše.