Sbírka řešených úloh

Krychle s hmotným bodem – hledání hlavních os setrvačnosti

Úloha číslo: 2250

Určete tenzor setrvačnosti homogenní krychle o délce hrany \(a\) a hmotnosti \(M\) vzhledem k jednomu z jejích vrcholů (viz. obrázek), jestliže je k vrcholu naproti přes stěnovou úhlopříčku připevněna kulička o hmotnosti \(m = \frac{M}{6}\) zanedbatelných rozměrů.

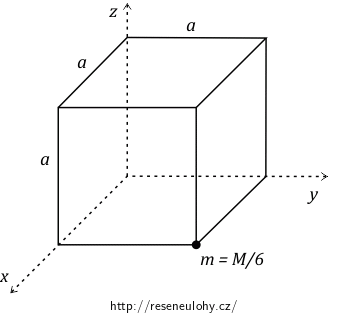
Najděte hlavní osy rotace a hlavní momenty setrvačnosti.

• Rozbor řešení úlohy

  Stručně si řekněme, jak budeme při řešení úlohy postupovat.

  Bude přehledné si nejdříve zvlášť spočítat tenzor setrvačnosti krychle vzhledem k jejímu vrcholu a tenzor setrvačnosti samotného hmotného bodu (kuličky) vzhledem k danému vrcholu.

  Následně určíme tenzor setrvačnosti celé soustavy vzhledem k danému vrcholu.

  Poté užijeme znalosti linérní algebry k určení vlastních vektorů a čísel matice tenzoru setrvačnosti a přiřadíme jim fyzikální význam.

• Tenzor setrvačnosti krychle – Nápověda 1

  Rozmyslete si, s jakými vztahy budete pracovat a které všechny veličiny potřebujete znát pro určení tenzoru setrvačnosti.

• Řešení – Nápověda 1

  Jelikož se jedná o homogenní krychli, bude vhodné uvažovat vztahy platné pro spojité prostředí. Tedy pro určení jednotlivých složek tenzoru setrvačnosti \(J_{jk}\) platí vztah:

  \[J_{jk}= \int_V {( \delta_{jk} \, r^2 - x_j \, x_k ) \rho} \, \mathrm{d}V,\]

  kde \(r\) je vzdálenost od počátku soustavy, \(\delta_{jk}\) je Kroneckerovo delta a souřadnice polohového vektoru \(x_i\) pro \(i=\) 1 až 3 jsou obecnějším zapsáním našich souřadnic \(x, \, y, \, z\).

  Poznámka: odvození tohoto vztahu viz například: Studijní text k teoretické mechanice tuhého tělesa.

  Potřebujeme znát i hustotu krychle \(\rho\). Protože je naše krychle homogenní, je tato hustota konstantní.

• Tenzor setrvačnosti krychle – Nápověda 2

  Vypočítejte postupně jednotlivé složky tenzoru setrvačnosti krychle a zapište je do matice.

  Rozmyslete si jednotlivé integrační meze a celkovou podobu našeho objemového integrálu.

• Řešení – Nápověda 2

  Z obrázku vidíme, že situace je velmi symetrická a rozložení vzhledem ke všem třem osám je stejné, z čehož plyne, že:

  (A) \(J_{xx} = J_{yy} = J_{zz}\);

  (B) \(J_{xy} = J_{xz} = J_{yz}\).

  Určeme nejprve moment setrvačnosti rotace okolo osy \(x\) odpovídajcí složce \(J_{xx}\):

  \[J_{xx}=J_{11}= \int_V {\left ( \delta_{11} \, r^2 - x_1 x_1 \right) \rho} \mathrm{d}V = \int_V {\left ( x^2 + y^2 + z^2 - x^2 \right ) \rho} \mathrm{d}V =\int_V {\left ( y^2 + z^2 \right ) \rho} \mathrm{d}V.\]

  Tento objemový integrál je třeba spočítat jako trojný integrál přes proměnné \(x, \, y\) a \(z\). Jelikož je střed naší soustavy ve vrcholu krychle, budeme integrovat od \(0\) po \(a\). Také využijeme toho, že hustota \(\rho\) je konstantní a je tudíž možné ji vytknout před integrál.

  \[J_{xx}= \rho \int_0^a \int_0^a \int_0^a {\left ( y^2 + z^2 \right )} \mathrm{d}x \, \mathrm{d}y \, \mathrm{d}z = \rho \int_0^a \int_0^a {\left ( y^2 + z^2 \right ) \left [ x \right ]_0^a} \mathrm{d}y \, \mathrm{d}z =\] \[= a \rho \int_0^a \int_0^a {\left ( y^2 + z^2 \right )} \mathrm{d}y \, \mathrm{d}z = a \rho \int_0^a {\left [ \frac {y^3}{3} + y \, z^2 \right]_0^a } \mathrm{d}z = a \rho \int_0^a {\left( \frac {a^3}{3} + a \, z^2 \right) } \mathrm{d}z =\] \[= a^2 \rho \int_0^a {\left ( \frac {a^2}{3} + z^2 \right)} \mathrm{d}z = a^2 \rho \left [ \frac {z \, a^2}{3} + \frac {z^3}{3} \right ]_0^a = a^2 \rho \frac {1}{3} \left [ 2 a^3 \right ] = \frac{2}{3} a^5 \rho = \] \[= \frac {2}{3} a^2 \rho a^3\]

  Výraz \(\rho \, a^3\) má význam celkové hmotnosti \(M\) naší krychle. Potom můžeme první složku tenzoru setrvačnosti zapsat jako:

  \[J_{xx} = \frac {2}{3} M a^2 .\]

  Tím jsme vyřešili složky tenzoru, které představují momenty setrvačnosti krychle vůči osám soustavy. Nyní se podíváme na deviační momenty, jež jsou všechny stejné a určíme člen \(J_{xy}\).

  \[J_{xy}=J_{12}= \int_V {\left ( \delta_{12} \, r^2 - x_1 x_2 \right) \rho} \mathrm{d}V = \int_V {\left ( -xy \right ) \rho} \mathrm{d}V = \] \[= - \rho \int_0^a \int_0^a \int_0^a {xy} \, \mathrm{d}x \, \mathrm{d}y \, \mathrm{d}z = - \rho \int_0^a {1} \mathrm{d}z \int_0^a x \mathrm{d}x \int_0^a y \mathrm{d}y = - \rho \left [ z \right ]_0^a \left[ \frac{x^2}{2} \right]_0^a \left[ \frac{y^2}{2} \right]_0^a =\] \[= - \frac{1}{4} \rho a^5 = - \frac{1}{4} M a^2\]

  Jelikož máme vypočítány všechny potřebné části tenzoru setrvačnosti homogenní krychle, již nám jen zbývá zapsat je do matice:

  \[J_{krychle}= \begin{pmatrix} \frac {2}{3} M a^2 & - \frac{1}{4} M a^2 & - \frac{1}{4} M a^2\\ - \frac{1}{4} M a^2 & \frac {2}{3} M a^2 & - \frac{1}{4} M a^2\\ - \frac{1}{4} M a^2 & - \frac{1}{4} M a^2 & \frac {2}{3} M a^2 \end{pmatrix} = \frac {1}{12} M a^2 \begin{pmatrix} 8 & -3 & -3\\ -3 & 8 & -3\\ -3 & -3 & 8 \end{pmatrix} .\]

• Tenzor setrvačnosti krychle – Odpověď

  Tenzor setrvačnosti homogenní krychle vzhledem k jednomu jejímu vrcholu má tvar:

  \[J_{krychle} = \frac {1}{12} M a^2 \begin{pmatrix} 8 & -3 & -3\\ -3 & 8 & -3\\ -3 & -3 & 8 \end{pmatrix} .\]

• Tenzor setrvačnosti hmotného bodu – Nápověda 1

  Nyní si spočítáme tenzor setrvačnosti samotného bodu o hmotnosti \(\frac{M}{6}\).

  Podívejte se na obrázek zadání a určete souřadnice hmotného bodu.

  Rozvažte, jakých vztahů budete užívat a jaké všechny veličiny k tomu budete potřebovat.

• Řešení – Nápověda 1

  Souřadnice hmotného bodu snadno určíme jako \(\left[ a,\,a,\,0 \right]\).

  Pro určení jednotlivých složek tenzoru setrvačnosti \(J_{jk}\) soustavy \(N\) hmotných bodů platí vztah:

  \[J_{jk}= \sum_{i=1}^{N}{ m_{(i)}( \delta_{jk} \, r_{(i)}^2 - x_{(i)j} \, x_{(i)k} )}\]

  kde \(i\) indexuje hmotné body o hmostnosti \(m_i\), \(r_i\) je vzdálenost \(i\)-tého bodu od počátku soustavy, \(\delta_{jk}\) je Kroneckerovo delta a souřadnice polohového vektoru \(x_{(i)l}\) pro \(l=\) 1 až 3 jsou obecnějším zapsáním našich souřadnic \(x, \, y, \, z\) \(i\)-tého bodu.

  Poznámka: Odvození tohoto vztahu viz například: Studijní text k teoretické mechanice tuhého tělesa.

  V našem případě se vztah ještě zjednodušší, protože máme pouze 1 hmotný bod.

  \[J_{jk}= m ( \delta_{jk} \, r^2 - x_j \, x_k )\]

• Tenzor setrvačnosti hmotného bodu – Nápověda 2

  Vypočítejte postupně jednotlivé složky tenzoru setrvačnosti hmotného bodu a zapište je do matice.

• Řešení – Nápověda 2

  Nejprve spočítejme složku \(J_{xx}\).

  \[J_{xx} = J_{11} = m ( \delta_{11} \, r^2 - x_1 \, x_1 ) = m ( x^2 + y^2 + z^2 - x^2 ) = m (y^2 + z^2 ) = m a^2\]

  Dále určíme složky \(J_{yy}\) a \(J_{zz}\).

  \[J_{yy} = m (x^2 + z^2 ) = m a^2\] \[J_{zz} = m (x^2 + y^2 ) = m ( a^2 + a^2 ) = 2 m a^2\]

  Poznámka: To je v souladu s klasickou mechanikou. Vzdálenost hmotného bodu od os \(x\) i \(y\) je \(a\), a tedy je moment setrvačnosti při rotaci okolo těchto os roven \(m a^2\). Vzdálenost hmotného bodu od osy \(z\) je \(a \sqrt 2\), a proto moment setrvačnosti při rotaci okolo osy \(z\) je \(2 m a^2\).

  Pokračujme vypočítáním deviačních momentů.

  \[J_{xy} = J_{12} = m ( \delta_{12} \, r^2 - x_1 \, x_2 ) = - m x y = - m a^2\] \[J_{xz} = - m x z = 0\] \[J_{yz} = - m y z = 0\]

  Známe všechny potřebné složky a víme, že matice tenzoru setrvačnosti je symetrická, tak již zbývá ji jen zapsat.

  \[J_m = m a^2 \begin{pmatrix} 1 & -1 & 0 \\ -1 & 1 & 0 \\ 0 & 0 & 2 \end{pmatrix} = \frac{M a^2}{6} \begin{pmatrix} 1 & -1 & 0 \\ -1 & 1 & 0 \\ 0 & 0 & 2 \end{pmatrix}\]

• Tenzor setrvačnosti hmotného bodu – Odpověď

  Tenzor setrvačnosti bodu o hmotnosti \(\frac{M}{6}\) vzhledem k počátku soustavy souřadnic je:

  \[J_{bod} = \frac{M a^2}{6} \begin{pmatrix} 1 & -1 & 0 \\ -1 & 1 & 0 \\ 0 & 0 & 2 \end{pmatrix}.\]

• Tenzor setrvačnosti celého systém – Nápověda

  Určeme tenzor setrvačnosti celého systému dohromady.

• Řešení nápovědy

  Tenzor setrvačnosti \(J\) celého systému, když známe tenzory setrvačnosti \(J_i\) jednotlivých částí systému, je jejich součtem.

  \[J = \sum_i {J_i}\]

  V našem případě bude pro celkový moment setrvačnosti \(J\) platit:

  \[J = J_{krych} + J_{bod} .\]

  Po dosazení dostaneme následující vztah.

  \[J = \frac {M a^2}{12} \begin{pmatrix} 8 & -3 & -3\\ -3 & 8 & -3\\ -3 & -3 & 8 \end{pmatrix} + \frac{M a^2}{6} \begin{pmatrix} 1 & -1 & 0 \\ -1 & 1 & 0 \\ 0 & 0 & 2 \end{pmatrix}\] \[J = \frac {M a^2}{12} \begin{pmatrix} 10 & -5 & -3\\ -5 & 10 & -3\\ -3 & -3 & 12 \end{pmatrix}\]

• Tenzor setrvačnosti celého systému – Odpověď

  Tenzor setrvačnosti \(J\) celého systému jsme určili jako:

  \[J = \frac {M a^2}{12} \begin{pmatrix} 10 & -5 & -3\\ -5 & 10 & -3\\ -3 & -3 & 12 \end{pmatrix}.\]

• Hlavní momenty setrvačnosti a hlavní osy rotace – Nápověda 1

  Nyní budeme hledat vlastní vektory a vlastní čísla tenzoru setrvačnosti.

  Zavzpomínejte, jak se hledají vlastní vektory matice. Osvěžte si pojmy: vlastní čísla, vlastní vektor a charakteristický polynom.

• Řešení – Nápověda 1

  Mějme čtvercovou matici \(A\) nad \(\mathbb{R}\). Pak vlastním vektorem \(\vec {v}\) matice \(A\) rozumíme nenulový vektor, pro nějž platí, že

  \[A \vec v = \lambda \vec v ,\]

  kde \(\lambda \in \mathbb{R}\). \(\lambda\) je vlastní číslo matice \(A\) příslušné vlastnímu vektoru \(\vec v\).

  \[A \vec v - \lambda \vec v = \vec o\] \[\left( A - \lambda \mathbb{E} \right) \vec v = \vec o\]

  Aby tato rovnice měla netriviální řešení, musí matice \(\left( A - \lambda \mathbb{E} \right)\) být singulární, tedy musí platit:

  \[\mathrm{det} \left| A - \lambda \mathbb{E} \right| = 0.\]

  Tuto rovnici nazýváme charakterictickým polynomem a užíváme ji pro hledání vlastních čísel.

  Jakmile nalezneme vlastní čísla, užijeme rovnice \(\left( A - \lambda \mathbb{E} \right) \vec v = \vec o\) k nalezení vlastních vektorů matice \(A\).

• Hlavní momenty setrvačnosti a hlavní osy rotace – Nápověda 2

  Najděte vlastní čísla a vektory matice

  \[\begin{pmatrix} 10 & -5 & -3 \\ -5 & 10 & -3 \\ -3 & -3 & 12 \end{pmatrix} .\]

• Řešení – Nápověda 2

  Najděme kořeny charakteristického polynomu této matice.

  \[\mathrm{det} \left| A - \lambda \mathbb{E} \right| = \begin{vmatrix} 10 - \lambda & -5 & -3 \\ -5 & 10 - \lambda & -3 \\ -3 & -3 & 12 - \lambda \end{vmatrix} = \] \[= \left( 12 - \lambda \right) \left( 10 - \lambda \right)^2 - 3 {\cdot} 3 \cdot 5 - 3 {\cdot} 3 \cdot 5 - 3 {\cdot} 3 \left( 10 - \lambda \right) - 3 {\cdot} 3 \left( 10 - \lambda \right) - 5 {\cdot} 5 \left( 12 - \lambda \right) = \] \[= \left( 12 - \lambda \right) \left( 100 - 20 \lambda + \lambda^2 \right) - 45 - 45 - 90 + 9 \lambda - 90 + 9 \lambda - 300 + 25 \lambda = \] \[=1200 -240 \lambda +12 \lambda^2 - 100 \lambda +20 \lambda^2 - \lambda^3 +43 \lambda - 570=\] \[= - \lambda^3 + 32 \lambda^2 - 297 \lambda + 630 = 0\] \[\lambda^3 - 32 \lambda^2 + 297 \lambda - 630 = 0\]

  Charakteristický polynom naší matice je kubická rovnice s nepříliš hezkými koeficienty. Takovouto rovnici lze řešit několika způsoby. Můžeme užít například Cardanovy vzorce nebo si pomoct Hornerovým schématem. Jelikož se jedná o fyzikálně vcelku hezkou situaci, můžeme doufat, že polynom bude mít malé celočíselné kořeny, a proto užijeme Hornerovo schéma.

  

  Zjistili jsme, že \(\lambda_1 = 3\) a dále proto stačí vyřešit kvadratickou rovnici ve tvaru:

  \[\lambda^2 - 29 \lambda + 210 = 0 .\]

  Opět se nejedná o kořeny, které by se daly snadno uhádnout, a proto použijeme univerzální metody řešení – diskriminantu.

  \[\lambda_{2{,}3} = \frac {29 \pm \sqrt {29^2 - 4 {\cdot} 210}}{2} = \frac {29 \pm 1 }{2}\]

  Tedy už známe všechna vlastní čísla.

  \[\lambda_1 = 3 \, ; \, \lambda_2 = 15 \, ; \, \lambda_3 = 14\]

  Najděme vlastní vektor \(\vec {v_1}^T = (x_1 , \, y_1 , \, z_1 )\) příslušný vlastnímu číslu \(\lambda_1\). Hledáme tedy netriviální řešení homogenní soustavy.

  \[\left( A - \lambda_1 \mathbb{E} \right) \vec {v_1} = \begin{pmatrix} 10 - \lambda_1 & -5 & -3 \\ -5 & 10 - \lambda_1 & -3 \\ -3 & -3 & 12 - \lambda_1 \end{pmatrix} \vec {v_1} = \vec o\] \[\begin{pmatrix} 7 & -5 & -3 \\ -5 & 7 & -3 \\ -3 & -3 & 9 \end{pmatrix} \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} = \vec o\tag{1}\]

  Nyní si trochu upravme naši matici.

  \[\begin{pmatrix} 7 & -5 & -3 \\ -5 & 7 & -3 \\ -3 & -3 & 9 \end{pmatrix} \sim \begin{pmatrix} 7 & -5 & -3 \\ -5 & 7 & -3 \\ -1 & -1 & 3 \end{pmatrix} \sim \begin{pmatrix} 0 & -12 & 18 \\ 0 & 12 & -18 \\ -1 & -1 & 3 \end{pmatrix} \sim \begin{pmatrix} 0 & 0 & 0 \\ 0 & 2 & -3 \\ 1 & 1 & -3 \end{pmatrix}\]

  Vraťme se zpět k naší rovnici (1).

  \[\begin{pmatrix} 0 & 0 & 0 \\ 0 & 2 & -3 \\ 1 & 1 & -3 \end{pmatrix} \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} = \vec o\]

  Máme soustavu rovnic:

  \[\begin{matrix} & 2 y_1 & - 3 z_1 & = 0 ; \\ x_1 & + y_1 & - 3 z_1 & = 0 . \end{matrix}\]

  Z první rovnice si můžeme vyjádřit \(2 y_1 = 3 z_1\) a dosadit do rovnice druhé.

  \[x_1 + y_1 - 2 y_1 = x_1 - y_1 = 0\] \[x_1 = y_1 = \frac{3}{2} z_1\]

  Tedy jsme dostali řešení soustavy, které je závislé na volbě jednoho parametru. Zvolme \(z_1 = 2\). Potom pro vektor \(\vec {v_1}\) příslušný vlastnímu číslu \(\lambda_1 = 3\) platí:

  \[\vec {v_1}^T = (3 , \, 3 , \, 2 ) \, .\]

  Dále hledejme obdobným způsobem vlastní vektor \(\vec {v_2}^T = (x_2 , \, y_2 , \, z_2 )\) příslušný vlastnímu číslu \(\lambda_2\).

  \[\left( A - \lambda_2 \mathbb{E} \right) \vec {v_2} = \begin{pmatrix} 10 - \lambda_2 & -5 & -3 \\ -5 & 10 - \lambda_2 & -3 \\ -3 & -3 & 12 - \lambda_2 \end{pmatrix} \vec {v_2} = \vec o\] \[\begin{pmatrix} -5 & -5 & -3 \\ -5 & -5 & -3 \\ -3 & -3 & -3 \end{pmatrix} \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} = \vec o\tag{2}\]

  Opět si trochu poupravujme naši matici.

  \[\begin{pmatrix} -5 & -5 & -3 \\ -5 & -5 & -3 \\ -3 & -3 & -3 \end{pmatrix} \sim \begin{pmatrix} 0 & 0 & 0 \\ 5 & 5 & 3 \\ 1 & 1 & 1 \end{pmatrix} \sim \begin{pmatrix} 0 & 0 & 0 \\ 2 & 2 & 0 \\ 1 & 1 & 1 \end{pmatrix} \sim \begin{pmatrix} 0 & 0 & 0 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \end{pmatrix}\]

  Tuto matici dosaďme do rovnice (2).

  \[\begin{pmatrix} 0 & 0 & 0 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \end{pmatrix} \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} = \vec o\]

  Tím jsme dostali soustavu rovnic pro vektor \(\vec v_2\).

  \[\begin{matrix} x_2 & + y_2 & & = 0 ; \\ x_2 & + y_2 & + z_2 & = 0 , \end{matrix}\]

  Z první rovnice plyne \(x_2 = - y_2\). Když toto dosadíme do druhé, zjistíme, že \(z_2 = 0\).

  Opět vidíme, že máme volnost ve volbě parametru, pro jednoduchost vezměme \(x_2 = 1\). Pak tedy platí pro vektor \(\vec {v_2}\) příslušný vlastnímu číslu \(\lambda_2 = 15\):

  \[\vec {v_2}^T = (1 , \, - 1 , \, 0 ) \, .\]

  Dále hledejme vlastní vektor \(\vec {v_3}^T = (x_3 , \, y_3 , \, z_3 )\) příslušný vlastnímu číslu \(\lambda_3\).

  \[\left( A - \lambda_3 \mathbb{E} \right) \vec {v_3} = \begin{pmatrix} 10 - \lambda_3 & -5 & -3 \\ -5 & 10 - \lambda_3 & -3 \\ -3 & -3 & 12 - \lambda_3 \end{pmatrix} \vec {v_3} = \vec o\] \[\begin{pmatrix} -4 & -5 & -3 \\ -5 & -4 & -3 \\ -3 & -3 & -2 \end{pmatrix} \begin{pmatrix} x_3 \\ y_3 \\ z_3 \end{pmatrix} = \vec o\tag{3}\]

  Matici si otesáme do hezčí podoby.

  \[\begin{pmatrix} 4 & 5 & 3 \\ 5 & 4 & 3 \\ 3 & 3 & 2 \end{pmatrix} \sim \begin{pmatrix} 1 & 2 & 1 \\ 2 & 1 & 1 \\ 3 & 3 & 2 \end{pmatrix} \sim \begin{pmatrix} 1 & 2 & 1 \\ 2 & 1 & 1 \\ 0 & 0 & 0 \end{pmatrix} \sim \begin{pmatrix} -1 & 1 & 0 \\ 2 & 1 & 1 \\ 0 & 0 & 0 \end{pmatrix}\]

  Tuto matici dosaďme do rovnice (3).

  \[\begin{pmatrix} -1 & 1 & 0 \\ 2 & 1 & 1 \\ 0 & 0 & 0 \end{pmatrix} \begin{pmatrix} x_3 \\ y_3 \\ z_3 \end{pmatrix} = \vec o\]

  Opět máme soustavu rovnic, tentokrát pro vektor \(\vec v_3\).

  \[\begin{matrix} - x_3 & + y_3 & & = 0 ; \\ 2 x_3 & + y_3 & + z_3 & = 0 , \end{matrix} \,\,\,\sim \,\,\, \begin{matrix} & x_3 & = y_3 ; \\ 2 x_3 & + y_3 & = - z_3 . \end{matrix}\]

  Dosazením první rovnice do druhé zjistíme vztah mezi \(x_3\) a \(z_3\).

  \[2 x_3 + y_3 = 3 x_3 = - z_3\] \[x_3 = y_3 = \frac{-1}{3} z_3\]

  Volbou \(z_3 = - 3\) určíme podobu vlastního vektoru \(\vec v_3\) příslušného vlastnímu číslu \(\lambda_3 = 14\).

  \[\vec {v_3}^T = (1 , \, 1 , \, -3 ) \, .\]

• Hlavní momenty setrvačnosti a hlavní osy rotace – Nápověda 3

  Přiřaďte výsledkům Nápovědy 2 fyzikální význam.

• Řešení – Nápověda 3

  Náš tenzor setrvačnosti celého systému měl tvar:

  \[J = \frac {M a^2}{12} \begin{pmatrix} 10 & -5 & -3\\ -5 & 10 & -3\\ -3 & -3 & 12 \end{pmatrix} = \frac {M a^2}{12} A . \]

  Určená vlastní čísla \(\lambda_i\) jsou vlastní čísla matice \(A\). Proto získáme hlavní momenty setrvačnosti \(J_i\) prostým přepočtem \(J_i = \lambda_i \, \frac{M a^2}{12}\). Nalezené vlastní vektory \(\vec {v_i}\) odpovídají směrům hlavních os rotace s příslušnými hlavními momenty setrvačnosti \(J_i\).

  \[\begin{matrix} J_1 = \frac{1}{4} M a^2 & & \vec {v_1}^T = (3 , \, 3 , \, 2 ) \\ J_2 = \frac{5}{4} M a^2 & & \vec {v_2}^T = (1 , \, -1 , \, 0 ) \\ J_3 = \frac{7}{6} M a^2 & & \vec {v_3}^T = (1 , \, 1 , \, -3 ) \end{matrix}\]

  Lze ověřit, že \(\vec {v_1}\) je kolmý na \(\vec {v_2}\) i \(\vec {v_3}\). Stejně tak \(\vec {v_2}\) je kolmý na \(\vec {v_3}\).

  3D náhled vytvořený pomocí programu GeoGebra.

• Poznámka k lineární algebře

  Opět trochu zavzpomínejme na lineární algebru.

  Máme-li matici \(A\), její vlastní čísla \(\lambda_i\) a vlastní vektory \(\vec v_i\), a když označíme \(P\) matici vytvořenou z vlastních vektorů \(\vec v_i\) zapsaných do sloupců, potom platí:

  \[P^{-1} \cdot A \cdot P = \begin{pmatrix} \lambda_1 & 0 & 0 \\ 0 & \lambda_2 & 0 \\ 0 & 0 & \lambda_3 \end{pmatrix} .\]

  Rozmysleme si, že \(P\) je matice přechodu od kanonické báze k bázi tvořené vlastními vektory.

  Tedy bychom měli dostat diagonalizovanou matici. Ověřme to tedy pro náš případ tenzoru setrvačnosti.

  Matice \(A\) je pro nás tenzorem setrvačnosti \(J_c\) celé soustavy.

  \[J_c = \frac {M a^2}{12} \begin{pmatrix} 10 & -5 & -3\\ -5 & 10 & -3\\ -3 & -3 & 12 \end{pmatrix}\]

  Vlastní čísla jsou pro nás hlavní momenty setrvačnosti \(J_i\) a k nim přísluší vlastní vektory \(\vec{v_i}\)

  \[\begin{matrix} J_1 = \frac{1}{4} M a^2 & & \vec {v_1}^T = (3 , \, 3 , \, 2 ) \\ J_2 = \frac{5}{4} M a^2 & & \vec {v_2}^T = (1 , \, -1 , \, 0 ) \\ J_3 = \frac{7}{6} M a^2 & & \vec {v_3}^T = (1 , \, 1 , \, -3 ) \end{matrix}\]

  V našem případě tedy matice \(P\) je ortogonální matice báze a má tvar:

  \[P = \begin{pmatrix} 3 & 1 & 1 \\ 3 & -1 & 1 \\ 2 & 0 & -3 \end{pmatrix}\]

  Najděme teď matici inverzního přechodu \(P^{-1}\).

  \[\left(\begin{matrix} 3 & 1 & 1 \\ 3 & -1 & 1 \\ 2 & 0 & -3 \end{matrix}\right| \left.\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}\right) \sim \left(\begin{matrix} 3 & 1 & 1 \\ 0 & -2 & 0 \\ 0 & -2 & -11 \end{matrix}\right| \left.\begin{matrix} 1 & 0 & 0 \\ -1 & 1 & 0 \\ -2 & 0 & 3 \end{matrix}\right) \sim \left(\begin{matrix} 3 & 1 & 1 \\ 0 & 2 & 0 \\ 0 & 0 & -11 \end{matrix}\right| \left.\begin{matrix} 1 & 0 & 0 \\ 1 & -1 & 0 \\ -1 & -1 & 3 \end{matrix}\right) \sim\] \[\sim \left(\begin{matrix} 3 & 1 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}\right| \left.\begin{matrix} 1 & 0 & 0 \\ \frac{1}{2} & -\frac{1}{2} & 0 \\ \frac{1}{11} & \frac{1}{11} & - \frac{3}{11} \end{matrix}\right) \sim \left(\begin{matrix} 3 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}\right| \left.\begin{matrix} \frac{1}{2} & \frac{1}{2} & 0 \\ \frac{1}{2} & -\frac{1}{2} & 0 \\ \frac{1}{11} & \frac{1}{11} & - \frac{3}{11} \end{matrix}\right) \sim \left(\begin{matrix} 3 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}\right| \left.\begin{matrix} \frac{9}{22} & \frac{9}{22} & \frac{3}{11} \\ \frac{1}{2} & -\frac{1}{2} & 0 \\ \frac{1}{11} & \frac{1}{11} & - \frac{3}{11} \end{matrix}\right) \sim \] \[\sim \left(\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}\right| \left.\begin{matrix} \frac{3}{22} & \frac{3}{22} & \frac{1}{11} \\ \frac{1}{2} & -\frac{1}{2} & 0 \\ \frac{1}{11} & \frac{1}{11} & - \frac{3}{11} \end{matrix}\right)\]

  Vypočítejme tedy součin \(P^{-1} \cdot J_c \cdot P\).

  \[P^{-1} \cdot J_c \cdot P = \begin{pmatrix} \frac{3}{22} & \frac{3}{22} & \frac{1}{11} \\ \frac{1}{2} & -\frac{1}{2} & 0 \\ \frac{1}{11} & \frac{1}{11} & - \frac{3}{11} \end{pmatrix} \cdot \frac {M a^2}{12} \begin{pmatrix} 10 & -5 & -3\\ -5 & 10 & -3\\ -3 & -3 & 12 \end{pmatrix} \cdot \begin{pmatrix} 3 & 1 & 1 \\ 3 & -1 & 1 \\ 2 & 0 & -3 \end{pmatrix} =\] \[= \frac {M a^2}{12} \begin{pmatrix} \frac{3}{22} & \frac{3}{22} & \frac{1}{11} \\ \frac{1}{2} & -\frac{1}{2} & 0 \\ \frac{1}{11} & \frac{1}{11} & - \frac{3}{11} \end{pmatrix} \cdot \begin{pmatrix} 9 & 15 & 14 \\ 9 & -15 & 14 \\ 6 & 0 & -42 \end{pmatrix} = \frac {M a^2}{12} \begin{pmatrix} 3 & 0 & 0 \\ 0 & 15 & 0 \\ 0 & 0 & 14 \end{pmatrix} \] \[P^{-1} \cdot J_c \cdot P = \begin{pmatrix} \frac{1}{4} M a^2 & 0 & 0 \\ 0 & \frac{5}{4} M a^2 & 0 \\ 0 & 0 & \frac{7}{6} M a^2 \end{pmatrix} = \begin{pmatrix} J_1 & 0 & 0 \\ 0 & J_2 & 0 \\ 0 & 0 & J_3 \end{pmatrix}\]

  Vidíme tedy, že vzhledem k naší ortogonální bázi \(\vec{v_1}\), \(\vec{v_2}\) a \(\vec{v_3}\) má matice tenzoru setrvačnosti opravdu diagonální tvar, kde na hlavní diagonále jsou hlavní momenty setrvačnosti.

• Hlavní momenty setrvačnosti a hlavní osy rotace - Odpověď

  Vektory \(\vec {v_i}\) určují hlavní osy rotace s příslušnými hlavními momenty setrvačnosti \(J_i\).

  \[\begin{matrix} J_1 = \frac{1}{4} M a^2 & & \vec {v_1}^T = (3 , \, 3 , \, 2 ) \\ J_2 = \frac{5}{4} M a^2 & & \vec {v_2}^T = (1 , \, -1 , \, 0 ) \\ J_3 = \frac{7}{6} M a^2 & & \vec {v_3}^T = (1 , \, 1 , \, -3 ) \end{matrix}\]