Válec na nakloněné rovině
Úloha číslo: 664
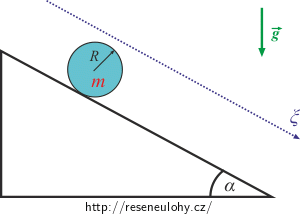
Po rovině nakloněné pod úhlem α se pohybuje homogenní válec o hmotnosti m a poloměru R. Tíhové zrychlení je g.
A) Je k vyjádření kinetické a potenciální energie válce potřeba znát všechny zadané veličiny (α, m, R, g) nebo na některé z nich energie nezávisí?
B) Bez výpočtu určete, zda rychlost válce bude při stejném gravitačním zrychlení a úhlu sklonu růst jinak, než rychlost hmotného bodu na nakloněné rovině.
C) Napište lagrangián válce na nakloněné rovině a vyřešte Lagrangeovy rovnice II. druhu.
Nápověda A1
K určení kinetické energie valícího se válce použijte Königovu větu.
Nápověda A2
Určete moment setrvačnosti homogenního válce o hmotnosti m a poloměru R vzhledem k ose procházející středy obou podstav. Podrobně je tento problém rozebrán v úloze Moment setrvačnosti válce.
Nápověda A3
Předpokládejme, že známe rychlost \(v\) translačního pohybu hmotného středu válce. Jak spočteme úhlovou rychlost ω rotačního pohybu?
Uvažujte, jaký je vztah mezi obvodovou rychlostí na povrchu válce a translační rychlostí hmotného středu.
Nápověda A4
Potenciální energie tuhého tělesa je dána výškou jeho těžiště. Nepotřebujeme tedy znát poloměr válce k určení výšky těžiště nad nakloněnou rovinou?
Řešení A
Kinetickou energii válce na nakloněné rovině určíme podle Königovy věty:
\[T = \frac{1}{2}mv^2 + \frac{1}{2}J\omega^2\ .\]Moment setrvačnosti homogenního válce vůči jeho ose je:
\[J = \frac{1}{2}mR^2\ .\](viz např. úloha Moment setrvačnosti válce)
Mezi rychlostí hmotného středu a úhlovou rychlostí rotace platí vztah (viz Řešení nápovědy A3):
\[v = \omega R\ .\]Pro celkovou kinetickou energii tedy dostáváme:
\[T = \frac{1}{2}mv^2 + \frac{1}{2}\cdot\frac{1}{2}mR^2\left(\frac{v}{R}\right)^2 = \frac{3}{4}mv^2\ .\]Vzdálenost těžiště homogenního válce od povrchu nakloněné roviny je konstantní. Lze ji tedy zahrnout do konstanty V0 vyjadřující rozdíl potenciální energie v počátku souřadnice a na nulové hladině. Platí tedy:
\[V = -mg\xi\sin \alpha + V_0\ .\]K určení kinetické energie a průběhu potenciální energie válce tedy nepotřebujeme znát jeho poloměr.
Nápověda B
Jaký je rozdíl mezi přeměnou potenciální energie v kinetickou u hmotného bodu a u válce? Jaké všechny druhy pohybu vykonává hmotný bod a jaké válec?
Řešení B
Vyjdeme ze zákona zachování mechanické energie:
\[\Delta T = -\Delta V\ ,\tag{1}\]kinetické energie hmotného bodu:
\[T = \frac{1}{2}mv^2\tag{2}\]a pomocí Königovy věty určené kinetické energie válce:
\[T = \frac{1}{2}mv^2 + \frac{1}{2}J\omega^2\ .\tag{3}\]Hmotný bod koná pouze pohyb translační, válec pohyb translační i rotační. Při stejném vkladu potenciální energie tedy padne na translační složku pohybu válce menší část energie, než je tomu u hmotného bodu – hmotný bod se nemusí roztáčet, resp. není nutno konat práci k jeho roztočení.
Za stejných podmínek se tedy hmotný bod pohybuje s větším zrychlením, než hmotný střed válce.
Nápověda C – Lagrangeova funkce
Lagrangeovu funkci L spočteme jako rozdíl kinetické energie T a potenciální energie V, které jsme již určili v předchozích částech:
\[L = T-V.\]Napište lagrangián pro náš případ. Za zobecněnou souřadnici zvolte, stejně jako v úloze Hmotný bod na nakloněné rovině, souřadnici ξ mířící dolů po povrchu nakloněné roviny. Tam je také podrobně rozepsána práce s ní.
Řešení – Lagrangeova funkce
Vyjádříme obě energie pomocí souřadnice ξ a její časové derivace:
\[T = \frac{3}{4}m\dot{\xi}^2\] \[V = -mg\xi sin \alpha + V_0\,.\]Odtud lagrangián:
\[L = \frac{3}{4}m\dot{\xi}^2 + mg\xi sin \alpha - V_0\,.\]Nápověda C – Lagrangeovy rovnice II. druhu
Připomeneme si tvar Lagrangeových rovnic II. druhu:
\[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial L}{\partial \dot{q}_{j}}\right)-\frac{\partial L}{\partial {q}_{j}} = 0\ ,\] pro j = 1, 2 ... n.
Podrobně jsou tvary rovnic a základy zacházení s nimi rozepsány v úloze Hmotný bod na nakloněné rovině.
Řešení – Lagrangeovy rovnice II. druhu
Připomeneme si tvar Lagrangeových rovnic II. druhu:
\[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial L}{\partial \dot{q}_{j}}\right)-\frac{\partial L}{\partial {q}_{j}} = 0\ ,\] pro j = 1, 2 ... n.
Nejdříve si připravíme potřebné derivace lagrangiánu:
\[\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial L}{\partial \dot{\xi}} = \frac{\mathrm{d}}{\mathrm{d}t}(\frac{3}{2}m\dot{\xi}) = \frac{3}{2}m\ddot{\xi}\] \[\frac{\partial L}{\partial \xi}= mg\sin\alpha\,.\]Dosadíme do obecného tvaru Lagrangeových rovnic II. druhu a upravíme:
\[\frac{3}{2}m\ddot{\xi} - mg\sin\alpha=0\] \[\ddot{\xi} = \frac{2}{3}g\sin\alpha\,.\]Po dvojím zintegrování podle času dostáváme:
\[\xi(t) = \frac{1}{3}gt^2\sin\alpha + v_0t + \xi_0\ .\]Vidíme, že se jedná o rovnoměrně zrychlený pohyb se zrychlením \(\frac{2}{3}g\sin\alpha\).
Skutečně tedy vyšlo zrychlení menší než u hmotného bodu.
Mějme ale na paměti, že tato rovnice platí pouze pro sklon roviny menší než 90°. V případě, že nastane volný pád, není mezi válcem a hmotným bodem rozdíl – těleso padá a nevalí se, takže je nutné upravit předpis pro kinetickou energii.
Odpověď
A) K vyjádření kinetické a potenciální energie homogenního válce nepotřebujeme ze zadaných veličin znát jeho poloměr.
B) Hmotný bod se při stejném sklonu nakloněné roviny a tíhového zrychlení bude pohybovat s větším zrychlením, než válec, protože není potřeba konat práci k jeho roztočení.
C) Lagrangeova funkce pro pohyb válce na nakloněné rovině má tvar:
\[L = \frac{3}{4}m\dot{\xi}^2 + mg\xi \sin \alpha - V_0\ .\]Řešením Lagrangeových rovnic II. druhu pro pohyb válce dostáváme:
\[\xi(t) = \frac{1}{3}gt^2\sin\alpha + v_0t + \xi_0\ .\]Vidíme, že se jedná o rovnoměrně zrychlený pohyb se zrychlením \(\frac{2}{3}g\sin\alpha\).
Skutečně tedy vyšlo zrychlení menší než u hmotného bodu.
Mějme ale na paměti, že tato rovnice platí pouze pro sklon roviny menší než 90°. V případě, že nastane volný pád, není mezi válcem a hmotným bodem rozdíl – těleso padá a nevalí se, takže je nutné upravit předpis pro kinetickou energii.


