Válec ve žlabu
Úloha číslo: 2271
Pevný homogenní válec hmotnosti \(m\) o poloměru \(r\) se bez prokluzu valí vnitřkem nepohyblivého většího válce o poloměru \(R\).

Najděte pohybovou rovnici menšího válce za předpokladu, že se příliš nevzdaluje od rovnovážné polohy. Najděte periodu \(T\) jeho kmitání.
Nápověda 1
Zvolte si soustavu souřadnic. Zamyslete se, kolik a jakých zobecněných souřadnic budete k řešení potřebovat.
Určete souřadnice hmotného středu válce ve vámi zvolené soustavě souřadnic.
Nápověda 2
K řešení pomocí Lagrangeových rovnic II. druhu potřebujete znalost lagrangiánu \(L\). Rozmyslete si, jaké veličiny potřebujete určit k získání lagrangiánu \(L\).
Celkové řešení
Soustavu souřadnic zvolíme tak, že počátek leží ve středu většího válce, osa \(x\) míří doprava ve vodorovném směru a osa \(y\) míří svisle dolů.
Jedná se o problém s jedním stupněm volnosti, vystačíme si tedy s jednou zobecněnou souřadnicí. Za zobecněnou souřadnici zvolme odchylku \(\varphi\) od svislého směru.
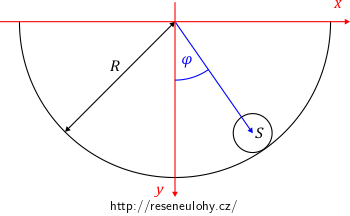
Z obrázku již pomocí goniometrických funkcí snadno vykoukáme souřadnice hmotného středu \(S\) válce.
\[S: \left[ \left( R - r \right) \sin \varphi \, ; \left( R - r \right) \cos \varphi \right]\]Lagrangián \(L\) je definován vztahem
\[L = T - V \, ,\]kde \(T\) je kinetická energie soustavy a \(V\) je potenciální energie soustavy.
Kinetická energie \(T\) válce se skládá ze dvou složek – energie translačního pohybu a rotačního pohybu. K určení energie translačního pohybu potřebujeme znát rychlost hmotného středu válce v závislosti na \(\varphi\). Jde o pohyb po kružnici o poloměru \(R - r\), tedy rychlost válce určíme ze vztahů pro obvodovou rychlost, známých z klasické mechaniky.
\[v = \dot{\varphi} \left( R - r \right)\] \[T_{translační} = \frac{m}{2} \left( R - r \right)^2 \dot{\varphi}^2 \]K určení kinetické energie rotačního pohybu potřebujeme znát úhlovou rychlost \(\omega_k\), jakou rotuje válec okolo osy procházející svým středem. Tu určíme díky předpokladu, že se válec pohybuje bez prokluzu, tedy se v čase \(t\) musí rovnat délky uraženého oblouku na obou kružnicích.
\[R \dot{\varphi} t = r \omega_k t\]Díky tomuto vztahu určíme kinetickou energii rotačního pohybu jako:
\[T_{rotační} = \frac{1}{2} J \omega_k^2 = \frac{J R^2}{2 r^2} \dot{\varphi}^2 \, .\]Protože moment setrvačnosti \(J\) válce je \(\frac{1}{2}mr^2\) můžeme energii rotačního pohybu přepsat jako:
\[T_{rotační} = \frac{m R^2}{4} \dot{\varphi}^2 \, .\]Celková kinetická energie je součtem energií rotačního a translačního pohybu.
\[T = \frac{m R^2}{4} \dot{\varphi}^2 + \frac{m}{2} \left( R - r \right)^2 \dot{\varphi}^2\] \[T = \frac{m R^2 + 2 m \left( R - r \right)^2}{4} \dot{\varphi}^2\]Kinetickou energii \(T\) jsme určili, je na čase zaobírat se potenciální energií \(V\).
Potenciální energie \(V\) homogenního gravitačního pole je v našem případě:
\[ V = - m g y ,\]kde \(g\) je gravitační zrychlení. Za \(y\) dosadíme souřadnici hmotného středu válce a budeme mít potenciální energii závislou na proměnné \(\varphi\).
\[V = - m g \left( R - r \right) \cos \varphi\]Protože se jedná o kmitání v okolí rovnovážné polohy, chceme potenciální energii aproximovat kvadratickou funkcí \(\varphi\).
\[V \approx - m g \left( R - r \right) \left( 1 - \frac{\varphi^2}{2} \right)\](Odůvodnění této aproximace viz Válec ve žlabu, Řešení – Nápověda 2.)Po této aproximaci budeme znát přibližný vztah pro naši potenciální energii \(V\).
\[V = \frac{m g \left( R - r \right)}{2}\varphi^2 - m g \left( R - r \right) = \frac{m g \left( R - r \right)}{2}\varphi^2 + \mathrm{konst.}\]Známe tedy vztah pro kinetickou energii \(T\) i vztah pro potenciální energii \(V\) a umíme tak určit i lagrangián \(L = T - V\).
\[L = \frac{m R^2 + 2 m \left( R - r \right)^2}{4} \dot{\varphi}^2 - \frac{m g \left( R - r \right)}{2}\varphi^2 - \mathrm{konst.}\]K nalezení pohybové rovnice užijeme Lagrangeových rovnic druhého druhu. Počet rovnic odpovídá počtu stupňů volnosti, a proto bude tato rovnice pouze jedna.
\[\frac{\mathrm{d}}{\mathrm{d}t} \left( \frac{\partial L}{\partial \dot{\varphi}} \right) - \frac{\partial L}{\partial \varphi} = 0 \]Nyní vypočítejme všechny nezbytné derivace našeho \(L\).
\[L = \frac{m R^2 + 2 m \left( R - r \right)^2}{4} \dot{\varphi}^2 - \frac{m g \left( R - r \right)}{2}\varphi^2 - \mathrm{konst.}\] \[\frac{\partial L}{\partial \varphi} = m g \left( R - r \right) \varphi \] \[\frac{\partial L}{\partial \dot{\varphi}} = \frac{m R^2 + 2 m \left( R - r \right)^2}{2} \dot{\varphi}\] \[\frac{\mathrm{d}}{\mathrm{d}t} \left( \frac{\partial L}{\partial \dot{\varphi}} \right) = \frac{m R^2 + 2 m \left( R - r \right)^2}{2} \ddot{\varphi}\]Potom tedy pro naši kuličku platí:
\[\frac{\mathrm{d}}{\mathrm{d}t} \left( \frac{\partial L}{\partial \dot{x}} \right) - \frac{\partial L}{\partial x} = \frac{m R^2 + 2 m \left( R - r \right)^2}{2} \ddot{\varphi} + m g \left( R - r \right) \varphi = 0 \, .\]Hledaná pohybová rovnice pro pohyb válce okolo rovnovážné polohy má tvar:
\[\ddot{\varphi} + \frac{2 g \left( R - r \right)}{R^2 + 2 \left( R - r \right)^2} \, \varphi = 0 \, .\]Jedná se o homogenní lineární diferenciální rovnici s konstantními koeficienty. Označíme-li \(\frac{2 g \left( R - r \right)}{R^2 + 2 \left( R - r \right)^2} = \omega^2\), pak lze řešení zapsat ve tvaru:
\[\varphi = A e^{i\omega t}\, .\]Pro periodu \(T\) platí vztah \(T = \frac{2 \pi}{\omega}\), a tedy perioda kmitání okolo rovnovážné polohy bude:
\[T = \frac{2 \pi}{\omega} = \pi \sqrt \frac{2 R^2 + 4 \left( R - r \right)^2}{g \left( R - r \right)} \, .\]Odpověď
Námi hledaná pohybová rovnice má tvar:
\[\ddot{\varphi} + \frac{2 g \left( R - r \right)}{R^2 + 2 \left( R - r \right)^2} \, \varphi = 0 \, ,\]což odpovídá kmitání okolo rovnovážné polohy s peridou
\[T = \pi \sqrt \frac{2 R^2 + 4 \left( R - r \right)^2}{g \left( R - r \right)} \, .\]

