Jednorozměrný harmonický oscilátor

Úloha číslo: 1232

Řešte jednorozměrný harmonický oscilátor pomocí Hamiltonových rovnic.

Harmonický oscilátor si představíme jako hmotný bod hmotnosti m na nehmotné pružině s tuhostí k.

Nápověda 1
Rozmyslete si, kolik má úloha stupňů volnosti a jaké zvolíte zobecněné souřadnice.
Řešení nápovědy 1
Úloha má pouze jeden stupeň volnosti.

Jako jedinou zobecněnou souřadnicí tedy můžeme zvolit přímo souřadnici x.
Nápověda 2
Hamiltonova funkce H se určuje z Lagrangeovy funkce L. Určete kinetickou a potenciální energii harmonického oscilátoru a napište příslušný lagrangián.
Řešení nápovědy 2
Harmonický oscilátor má pouze kinetickou energii posuvného pohybu T:
\[T=\frac{1}{2}m\dot{x}^2.\]
Jedinou složkou potenciální energie je potenciální energie pružnosti V:
\[V=\frac{1}{2}kx^2.\]
Z toho již můžeme sestavit lagrangián:
\[L=T-V=\frac{1}{2}m\dot{x}^2-\frac{1}{2}kx^2.\]
Nápověda 3
Hamiltonova funkce H je definována obecně jako:
\[H=\sum_{i=1}^n{p_i\dot{q_i}}-L,\]
kde q_i je zobecněná souřadnice a p_i je příslušná zobecněná hybnost.

Spočtěte Hamiltonovu funkci.

Zobecněnou hybnost p_i spočítáme podle vzorce:
\[p_i=\frac{\partial{L}}{\partial{\dot{q_i}}}.\]
Řešení nápovědy 3
Hamiltonova funkce H bude v našem případě vypadat jako:
\[H=p\dot{x}-L.\]
Zobecněnou hybnost p spočítáme podle vzorce:
\[p=\frac{\partial{L}}{\partial{\dot{x}}}.\]
Provedeme naznačenou parciální derivaci a získáváme:
\[p=\frac{\partial{L}}{\partial{\dot{x}}}=\frac{\partial{\left(\frac{1}{2}m\dot{x}^2-\frac{1}{2}kx^2\right)}}{\partial{\dot{x}}}=m\dot{x}.\]
Vidíme tedy, že zobecněná hybnost se v tomto případě rovná hybnosti, kterou známe z klasické mechaniky. To je dáno tím, že jako zobecněnou souřadnici jsme použili přímo jednu z kartézských souřadnic.

Dosadíme za hybnost p a lagrangián L:
\[H=p\dot{x}-L=m\dot{x}^2-\frac{1}{2}m\dot{x}^2+\frac{1}{2}kx^2=\frac{1}{2}m\dot{x}^2+\frac{1}{2}kx^2.\]
Přirozené proměnné hamiltoniánu jsou zobecněné souřadnice a hybnosti, proto výsledek ještě upravíme tak, aby v něm nevystupovala zobecněná rychlost \(\dot{x},\) ale zobecněná hybnost p:
\[H=\frac{p^2}{2m}+\frac{1}{2}kx^2.\]
Hamiltonián vyšel roven celkové mechanické energii, tedy jako součet kinetické a potenciální energie. Lze obecně ukázat, že toto nastane vždy, když není lagrangián explicitně závislý na čase.
Nápověda 4
Napište Hamiltonovy kanonické rovnice obecně a dosaďte do nich.
Řešení nápovědy 4 – obecný tvar rovnic
Hamiltonovy kanonické rovnice mají tvar:
\[\dot{q_i}=\frac{\partial{H}}{\partial{p_i}},\] \[\dot{p_i}=-\frac{\partial{H}}{\partial{q_i}},\] \[\frac{\partial{L}}{\partial{t}}=-\frac{\partial{H}}{\partial{t}}.\]
Poslední rovnice se uplatní pouze v případě explicitní závislosti lagrangiánu a hamiltoniánu na čase. (V našem případě ji tedy nemusíme uvažovat.)
Řešení nápovědy 4 – dosazení
V našem případě máme jedinou (zobecněnou) souřadnici x a k ní příslušnou (zobecněnou) hybnost p. Rovnice tedy nabývají tvaru:
\[\dot{x}=\frac{\partial{H}}{\partial{p}},\] \[\dot{p}=-\frac{\partial{H}}{\partial{x}}.\]
Provedeme naznačené derivace a získáváme:
\[\dot{x}=\frac{p}{m},\] \[\dot{p}=-kx.\]
Jako pohybové rovnice jsme tedy dostali soustavu dvou lineárních diferenciálních rovnic prvního řádu. Můžeme ji dosazením derivace první rovnice do druhé také přepsat do známého tvaru:
\[\ddot{x}+\frac{k}{m}x=0.\]
Nápověda 5
Napište řešení pohybové rovnice z minulé nápovědy a odvoďte vztah pro časový vývoj hybnosti p.
Řešení nápovědy 5
V minulé nápovědě jsme získali rovnici:
\[\ddot{x}+\frac{k}{m}x=0.\]
Řešení této rovnice známe:

Viz úloha Kladka na pružině, Komentář – řešení pohybové rovnice.
\[x=A\cos{(\omega t+\varphi_0)},\]
kde konstanta A je amplituda, φ₀ je počáteční fáze a ω je úhlová rychlost zavedená vztahem:
\[\omega=\sqrt{\frac{k}{m}}.\]
Nyní můžeme dosadit do vztahu pro hybnost p a získáváme:
\[p=m\dot{x}=-m\omega A\sin{(\omega t+\varphi_0)}.\]
Celkové řešení
Úloha má pouze jeden stupeň volnosti.

Za jedinou zobecněnou souřadnicí můžeme zvolit přímo souřadnici x.

Napíšeme kinetickou energii T a potenciální energii V harmonického oscilátoru:
\[T=\frac{1}{2}m\dot{x}^2,\] \[V=\frac{1}{2}kx^2.\]
Spočítáme lagrangián L:
\[L=T-V=\frac{1}{2}m\dot{x}^2-\frac{1}{2}kx^2.\]
Abychom mohli vyjádřit Hamiltonovu funkci H, která v našem případě vypadá jako:
\[H=p\dot{x}-L,\]
musíme znát zobecněnou hybnost p. Tu spočítáme podle vzorce:
\[p=\frac{\partial{L}}{\partial{\dot{x}}} = m\dot{x}.\]
Vidíme tedy, že zobecněná hybnost má tvar hybnosti, kterou známe z klasické mechaniky.

Dosadíme do vyjádření hamiltoniánu H za hybnost p a lagrangián L a dostáváme:
\[H=\frac{1}{2}m\dot{x}^2+\frac{1}{2}kx^2.\]
Přirozené proměnné hamiltoniánu jsou zobecněné souřadnice a hybnosti, proto výsledek ještě upravíme tak, aby v něm nevystupovala zobecněná rychlost \(\dot{x}\), ale zobecněná hybnost p:
\[H=\frac{p^2}{2m}+\frac{1}{2}kx^2.\]
Hamiltonián vyšel roven celkové mechanické energii, tedy jako součet kinetické a potenciální energie. Toto nastane vždy, když není lagrangián explicitně závislý na čase.

Hamiltoniánu využijeme k napsání Hamiltonových kanonických rovnic, které mají obecně tvar:
\[\dot{q_i}=\frac{\partial{H}}{\partial{p_i}},\] \[\dot{p_i}=-\frac{\partial{H}}{\partial{q_i}}.\]
V našem případě máme jedinou (zobecněnou) souřadnici x a k ní příslušnou (zobecněnou) hybnost p. Rovnice tedy nabývají tvaru:
\[\dot{x}=\frac{\partial{H}}{\partial{p}},\] \[\dot{p}=-\frac{\partial{H}}{\partial{x}}.\]
Provedeme naznačené derivace a získáváme:
\[\dot{x}=\frac{p}{m},\] \[\dot{p}=-kx.\]
Jako pohybové rovnice jsme tedy dostali soustavu dvou lineárních diferenciálních rovnic prvního řádu. Můžeme ji dosazením derivace první rovnice do druhé také přepsat do známého tvaru:
\[\ddot{x}+\frac{k}{m}x=0.\]
Řešení této rovnice známe. Viz úloha Kladka na pružině, Komentář – řešení pohybové rovnice.
\[x=A\cos{(\omega t+\varphi_0)},\]
kde konstanta A je amplituda, φ₀ je počáteční fáze a ω je úhlová rychlost zavedená vztahem:
\[\omega=\sqrt{\frac{k}{m}}.\]
Nyní můžeme dosadit do vztahu pro hybnost p a získáme:
\[p=m\dot{x}=-m\omega A\sin{(\omega t+\varphi_0)}.\]
Odpověď
Hamiltonova funkce H harmonického oscilátoru je:
\[H=\frac{p^2}{2m}+\frac{1}{2}kx^2.\]
Hamiltonovy kanonické rovnice mají tvar:
\[\dot{x}=\frac{p}{m},\] \[\dot{p}=-kx.\]
Jejich řešení pro souřadnici x a p má tvar:
\[x=A\cos{(\omega t+\varphi_0)},\] \[p=-m\omega A\sin{(\omega t+\varphi_0)}.\]
Komentář – trajektorie ve fázovém prostoru
Fázový prostor je prostor všech stavů systému. V našem případě máme pouze jednorozměrný pohyb, stav oscilátoru je tedy jednoznačně popsán jeho polohou (zobecněnou souřadnicí) a (zobecněnou) hybností. Prostor tedy bude dvoudimenzionální, na jednu osu naneseme souřadnici x a na druhou hybnost p, pro které jsme získali vyjádření:
\[x=A\cos{(\omega t+\varphi_0)},\] \[p=-m\omega A\sin{(\omega t+\varphi_0)}.\]
Abychom získali trajektorii ve fázovém prostoru, musíme z rovnice pro hybnost p a souřadnici x vyloučit čas. Využijeme gonimetrického vzorce sin²α + cos²α = 1. Obě rovnice výše tedy nejprve umocníme na druhou a vyjádříme příslušné kvadráty goniometrických funkcí:
\[\cos^2{(\omega t+\varphi_0)}=\frac{x^2}{A^2},\] \[\sin^2{(\omega t+\varphi_0)}=\frac{p^2}{m^2\omega^2 A^2}\]
Rovnice sečteme a získáme:
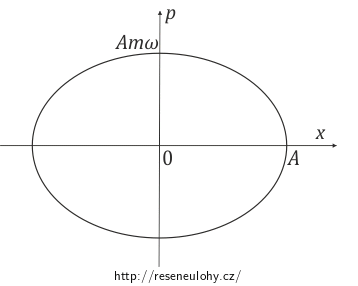
\[\frac{x^2}{A^2}+\frac{p^2}{m^2\omega^2 A^2}=1.\]
Toto je středová rovnice elipsy se středem v počátku soustavy souřadnic a poloosami o velikostech A a Amω.

Harmonický oscilátor se tedy ve fázovém prostoru pohybuje po elipse.