Soustava kladek
Úloha číslo: 638
Nalezněte lagrangián soustavy kladek na obrázku a vyřešte pohybové rovnice pro případ, že
A) kladky jsou nehmotné.
B) kladky jsou plné válce o hmotnostech m3 a m4.
Závaží můžeme považovat za hmotné body, kladky se pohybují bez tření. Celková délka provázku je l, rovněž ho považujeme za nehmotný. Pro zjednodušení uvažujme, že se závaží mohou pohybovat pouze nahoru nebo dolů (nemohou se houpat).

Nápověda 1
Soustava je sice tvořena několika objekty, ale kolik má ve skutečnosti stupňů volnosti?
Nápověda 2
Soustava má sice jen jeden stupeň volnosti a tedy nakonec postačí jediná zobecněná souřadnice, ale z praktických důvodů by možná bylo vhodnější zvolit souřadnic víc, systém jimi popsat a potom teprve převést na jedinou.
Navrhněte takové souřadnice a napište transformační vztahy mezi nimi. Nezapomeňte, že budeme potřebovat nejen vztah souřadnic, ale i jejich časových derivací!
Nápověda 3
Určete kinetickou energii obou závaží v souřadnicích x, y a tu pak vyjádřete pomocí souřadnice y.
Nápověda 4
Určete potenciální energii závaží a rozmyslete, které členy výsledného výrazu budou a které nebudou pro Lagrangeovy rovnice II. druhu podstatné.
Řešení – lagrangián A)
Soustava má jen jeden stupeň volnosti. Zvolíme zobecněné souřadnice x, y (viz obrázek), pro které platí:
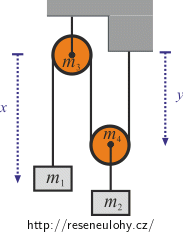
\[x=l-2y\] \[\dot{x}=-2\dot{y}\]Jejich pomocí vyjádříme kinetickou a potenciální energii. Pak vztahy napíšeme pouze s použitím jedné z nich, a to souřadnice y
\[T = \frac{1}{2}m_1\dot{x}^2 + \frac{1}{2}m_2\dot{y}^2 = 2m_1\dot{y}^2 + \frac{1}{2}m_2\dot{y}^2 = \left(2m_1+ \frac{1}{2}m_2\right)\dot{y}^2\] \[V = -m_1gx - m_2gy = -m_1g(l-2y) - m_2gy = (2m_1-m_2)gy-mgl.\]Pomineme konstantní členy a napíšeme lagrangián:
\[L_1(y) = \left(2m_1+ \frac{1}{2}m_2\right)\dot{y}^2 - (2m_1-m_2)gy\ .\]Pokud bychom vyjádřili lagrangián pomocí x, dostaneme:
\[L_1(x)' = \frac{1}{8}(4m_1+ m_2)\dot{x}^2 - \frac{1}{2}(m_2-2m_1)gx\ .\](Čárkou je tento lagrangián značen, protože se od L1(y) liší krom použité souřadnice ještě o konstantu.)
Nápověda 5
Napište Lagrangeovy rovnice II. druhu. Připomeneme si jejich obecný tvar:
\[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial L}{\partial \dot{q}_{j}}\right)-\frac{\partial L}{\partial {q}_{j}} = 0\ ,\] pro j = 1, 2 ... n .
Protože máme pouze jeden stupeň volnosti, budeme mít jenom jednu rovnici.
Pohybová rovnice A) a její řešení
Z Lagrangeovy rovnice na základě Lagrangeovy funkce L1(y) jsme dospěli ke vztahu:
\[\ddot{y} = \frac{m_2-2m_1}{4m_1+m_2}g\ .\]Po dvojím zintegrování dostáváme:
\[y = \frac{m_2-2m_1}{8m_1+2m_2}gt^2 + v_{y0}t + y_0\](o nalézání významu integračních konstant viz Hmotný bod na nakloněné rovině)
Analogicky z L1'(x) dostáváme:
\[x = \frac{2m_1-m_2}{4m_1+m_2}gt^2 + v_{x0}t + x_0\ .\]Je vidět, že se v obou případech jedná o rovnoměrně zrychlený pohyb. Směr pohybu závaží bude vždy opačný a závaží na volné kladce se pohybuje s polovičním zrychlením oproti závaží na pevné kladce.
Nápověda 6
Jak se změní už spočtený lagrangián, když budeme nyní předpokládat, že kladky jsou plné válce? Je potřeba ho celý přepisovat?
Nápověda 7
Pročtěte si způsob určování kinetické energie válce u úlohy Válec na nakloněné rovině.
Vykonávají kladky translační i rotační pohyb?
Nápověda 8
Spočtěte potenciální energii kladek. Nezapomínejte, že nám stačí pouze členy závislé na x nebo y. Konstantní členy můžeme bez újmy na obecnosti zanedbat, resp. položit rovny nule.
Řešení – lagrangián B)
Stačí nám pouze přičíst nové členy reprezentující energie kladek k L1.
\[L_2 (y) = L_1(y) + m_3\dot{y}^2 + \frac{3}{4}m_4\dot{y}^2 + m_4gy\] \[L_2(y) = \frac{1}{4}(8m_1+ 2m_2 + 4m_3 + 3m_4)\dot{y}^2 + (m_2 + m_4 -2m_1)gy\ ,\]resp.
\[L_2(x)' = \frac{1}{16}(8m_1+ 2m_2 + 4m_3 + 3m_4)\dot{x}^2 - \frac{1}{2}(m_2 + m_4 -2m_1)gx\ .\](Čárka opět kvůli tomu, že se lagrangiány liší o konstantu.)
Pohybová rovnice B) a její řešení
Derivacemi druhého lagrangiánu dospějeme k pohybové rovnici:
\[(4m_1+m_2 + 2m_3 + \frac{3}{2}m_4)\ddot{y} - (m_2 + m_4 -2m_1)g = 0\] \[\ddot{y} = \frac{m_2 + m_4 -2m_1}{4m_1+m_2 + 2m_3 + \frac{3}{2}m_4}g\]Dvakrát zintegrujeme a dostáváme.
\[y = \frac{m_2 + m_4 -2m_1}{8m_1+2m_2 + 4m_3 + 3m_4}gt^2 + v_{y0}t + y_0\ .\]Analogicky:
\[x = \frac{4m_1 - 2m_2 - 2m_4}{8m_1+2m_2 + 4m_3 + 3m_4}gt^2 + v_{x0}t + x_0\ .\]I zde se evidentně jedná o pohyb rovnoměrně zrychlený, zrychlení závaží na volné kladce je opět poloviční oproti závaží na volné kladce a závaží se pohybují proti sobě.
Odpověď

1) V případě, že považujeme kladky za nehmotné, dostáváme lagrangiány:
\[L_1(y) = \left(2m_1+ \frac{1}{2}m_2\right)\dot{y}^2 - (2m_1-m_2)gy\ ,\] \[L_1(x)' = \frac{1}{8}(4m_1+ m_2)\dot{x}^2 - \frac{1}{2}(m_2-2m_1)gx\ .\](Čárkou je tento lagrangián značen, protože se od L1(y) liší krom použité souřadnice ještě o konstantu.)
Řešením pohybové rovnice je funkce:
\[y = \frac{m_2-2m_1}{8m_1+2m_2}gt^2 + v_{y0}t + y_0\ .\]Analogicky z L1(x) dostáváme:
\[x = \frac{2m_1-m_2}{4m_1+m_2}gt^2 + v_{x0}t + x_0\ .\]2) Pro kladky uvažované jako plné válce obdržíme lagrangiány:
\[L_2(y) = \left(2m_1+ \frac{1}{2}m_2 + m_3 + \frac{3}{4}m_4\right)\dot{y}^2 + (m_2 + m_4 -2m_1)gy\ ,\] \[L_2(x)' = \frac{1}{16}(8m_1+ 2m_2 + 4m_3 + 3m_4)\dot{x}^2 - \frac{1}{2}(m_2 + m_4 -2m_1)gx\ .\]a řešení pohybové rovnice:
\[y = \frac{m_2 + m_4 -2m_1}{8m_1+2m_2 + 4m_3 + 3m_4}gt^2 + v_{y0}t + y_0\ ,\] \[x = \frac{4m_1 - 2m_2 - 2m_4}{8m_1+2m_2 + 4m_3 + 3m_4}gt^2 + v_{x0}t + x_0\ .\]Z vazebné podmínky pro integrační konstanty, resp. počáteční rychlosti a polohy, plynou vzájemné vztahy:
\[v_x = -2v_y\] \[x_0 = l -2y_0 l.\]


