Wattův regulátor
Úloha číslo: 922
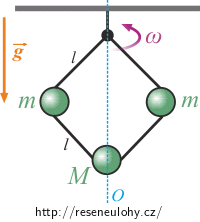
Na obrázku vidíte zjednodušené schéma tzv. Wattova odstředivého regulátoru. Ramena délky l jsou na pevný závěs přichycena kloubem, takže se mohou ohýbat (tření zanedbáme). Celá soustava se otáčí kolem osy O tak, že rovina, ve které se pohybují menší závaží o hmotnosti m, je kolmá na nákresnu i na osu O. Vše se děje v homogenním gravitačním poli tíhové zrychlení míří svisle dolů.
Najděte rovnovážnou polohu závaží o hmotnosti M při dané úhlové rychlosti otáčení ω.
Nápověda 1
Pokud úlohu budeme řešit z hlediska neinerciální soustavy, která se točí společně s osou otáčení, pak nám úlohu stačí řešit de facto jen ve dvou rozměrech (tj. v rovině).
Kolik má tedy soustava stupňů volnosti?
Nápověda 2
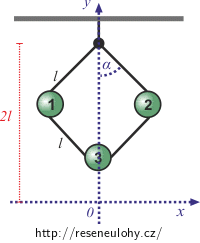
Popište polohy jednotlivých závaží pomocí úhlu α. Pro konečné řešení úlohy to není až tak podstatné, ale zvolme počátek kartézské soustavy souřadnic tak, aby odpovídal poloze závaží č. 3 při nulovém úhlu α.
Určete i složky vektorů infinitezimálně malého posunutí slučitelného s vazbami pro každé závaží.
Nápověda 3
Vyjádřete pomocí úhlu α složky vektorů aktivních sil působících na jednotlivá závaží.
Těmi jsou zde síla tíhová a síla odstředivá (pozor, nikoli dostředivá, ale skutečně odstředivá – jsme v neinerciální soustavě!).
Nápověda 4
Zobecněný princip virtuální práce lze zapsat vztahem:
\[\sum_{i=1}^{N} \vec{F}_i \cdot \delta \vec{r}_i = 0,\]kde N je počet hmotných bodů, které soustavu tvoří, \(\vec{F}_i\) je výslednice aktivních sil působících na i-tý bod a \(\delta \vec{r}_i\) je jeho infinitezimálně malé, vratné posunutí slučitelné s vazbami.
Teď již stačí dosadit do výše uvedeného vztahu a vyřešit získanou rovnici.
Řešení
Soustava má jen jeden stupeň volnosti. Jako parametr si zvolíme úhel α (viz obrázek).

Pro polohy jednotlivých závaží tedy platí:
Závaží x y 1 \[x_1 = -l\sin \alpha\] \[y_1 = l(2-\cos \alpha)\] 2 \[x_2 = l\sin \alpha\] \[y_2 = l(2-\cos \alpha)\] 3 \[x_3 = 0\] \[y_3 = 2l(1-\cos \alpha)\] A odtud derivováním dostáváme:
Závaží dx dy 1 \[dx_1 = -l\cos \alpha \ \mathrm{d}\alpha\] \[dy_1 = l\sin \alpha \ \mathrm{d}\alpha\] 2 \[dx_2 = l\cos \alpha \ \mathrm{d}\alpha\] \[dy_2 = l\sin \alpha \ \mathrm{d}\alpha\] 3 \[dx_3 = 0\] \[dy_3 = 2l\sin \alpha \ \mathrm{d}\alpha\] Odstředivá a gravitační síla jsou na sebe kolmé. Můžeme tedy jednoduše psát už složky výslednic působících na jednotlivá závaží:
Závaží Fx Fy 1 \[F_{x1} = -ml\omega^2\sin \alpha\] \[F_{y1} = -mg\] 2 \[F_{x2} = ml\omega^2\sin \alpha\] \[F_{y1} = -mg\] 3 \[F_{x3} = 0\] \[F_{y3} = -Mg\] Máme již všechny informace, abychom mohli dosadit do zobecněného principu virtuální práce:
\[2ml^2\omega^2\sin \alpha \cos \alpha \ \mathrm{d}\alpha-2mgl\sin \alpha \ \mathrm{d}\alpha-2Mgl\sin \alpha \ \mathrm{d}\alpha = 0\ .\tag{1}\]Upravíme:
\[\sin \alpha(ml\omega^2 \cos \alpha - mg - Mg) = 0\ .\]Jedním řešením tedy bude:
\[\sin \alpha_1 = 0\] \[\alpha_1 = 0\]a odtud pro souřadnici y3:
\[y_{31}=0\ .\]Podívejme se nyní na druhý činitel rovnice v součinovém tvaru:
\[ml\omega^2 \cos \alpha - mg - Mg = 0\ .\]Upravíme:
\[\cos \alpha = \left(\frac{M+m}{m}\right)\frac{g}{l\omega^2}\ .\]Odtud pro hledanou souřadnici y3:
\[y_{32} = 2l(1-\cos \alpha) = 2l\left[1-\left(\frac{M+m}{m}\right)\frac{g}{l\omega^2}\right]=2\left[l - \left(\frac{M+m}{m}\right)\frac{g}{\omega^2}\right]\ .\]Je zřejmé, že řešení y31 bude existovat vždy, zatímco řešení y32 nemusí, protože hodnota kosinu nemůže být větší než 1, což by se ovšem při určitých otáčkách (hodnotě ω) stalo.
Existují tedy určité mezní otáčky, resp. mezní úhlová rychlost ω0, při které začíná existovat i druhé řešení rovnice. Z podmínek existence funkce kosinus pro ni platí:
\[\omega_0 = \sqrt{\frac{M+m}{m}}\sqrt{\frac{g}{l}}\ .\]Odtud tedy možnosti řešení v závislosti na úhlové rychlosti otáčení:
Úhlová rychlost Řešení 1 Řešení 2 \[\omega \ < \ \omega_0\] Stabilní poloha \[y_{31} = 0\]
Neexistuje
\[\omega \ \geq \ \omega_0\] Labilní poloha \[y_{31} = 0\]
Stabilní poloha \[y_{32}(\omega)=2\left[l - \left(\frac{M+m}{m}\right)\frac{g}{\omega^2}\right]\]
Při malých otáčkách je jedinou rovnovážnou polohou poloha s nulovým úhlem α. Při překročení mezní rychlosti, tj. při vyšších otáčkách se z ní stane poloha labilní. Pokud se totiž v tomto případě závaží č. 3 nadzvedne, zvětší se poloměr otáčení druhých dvou závaží, čímž vzroste velikost odstředivé síly a závaží č. 3 už se do původní polohy samovolně nevrátí.
Odpověď
Existuje více řešení této úlohy v závislosti na úhlové rychlosti otáčení regulátoru ω:
Úhlová rychlost Řešení 1 Řešení 2 \[\omega \ < \ \omega_0\] Stabilní poloha \[y_{31} = 0\]
Neexistuje
\[\omega \ \geq \ \omega_0\] Labilní poloha \[y_{31} = 0\]
Stabilní poloha \[y_{32}(\omega)=2\left[l - \left(\frac{M+m}{m}\right)\frac{g}{\omega^2}\right]\]
kde y je výška, do které se zvedne závaží o hmotnosti M (číslice v indexu označují po řadě číslo závaží a číslo řešení) a ω0 je mezní úhlová rychlost, pro kterou platí:
\[\omega_0 = \sqrt{\frac{M+m}{m}}\sqrt{\frac{g}{l}}.\]Komentář – inženýrský význam
Wattův regulátor v podobě, v jaké byl v této úloze popsán, se nejčastěji používal k regulaci otáček parního stroje. Závaží č. 3 zde slouží jako model zařízení, které se stoupajícími otáčkami postupně přivíralo regulační ventil a snižovalo tak přívod páry.
Obrázky
Laboratorní model Wattova regulátoru

Zdroj: TimeRime (http://timerime.com/es/evento/1389805/Regulador++Centrifugo/)
Náčrtek funkce Wattova regulátoru
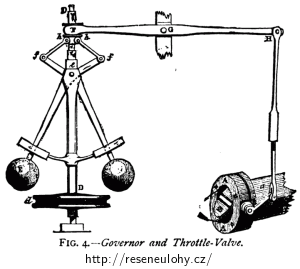
Zdroj: Wikipedie (http://en.wikipedia.org/wiki/File:Centrifugal_governor.png)
Wattův regulátor v činnosti
U tohoto modelu je jako síla působící proti nadzvedávání závaží použita kromě gravitační síly i síla pružnosti pružiny.

Foto: David Mindell, zdroj: spectrum.ieee.org (http://spectrum.ieee.org/green-tech/advanced-cars/slideshow-victorian-hacking/0)


