Tyč mezi dvěma šikmými stěnami

Úloha číslo: 1042

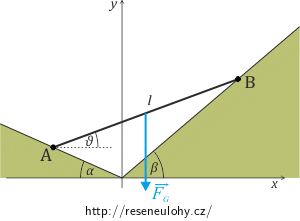
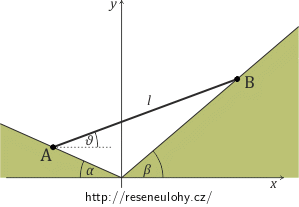
Nechť průsečnice dvou dokonale hladkých rovinných stěn leží ve vodorovné rovině, s níž tyto stěny svírají úhly α a β. Tyč délky l se opírá o tyto stěny svými konci A, B tak, že celá leží ve svislé rovině kolmé na průsečnici (viz obrázek).

Určete úhel \( \vartheta \), který svírá tyč v rovnovážné poloze s vodorovnou rovinou.

Nápověda 1
Nejprve si rozmyslete, jaké síly budou na tyč působit a zakreslete si je.
Řešení nápovědy 1
Na tyč bude působit vtištěná tíhová síla a reakční síly v místech dotyku tyče s rovinami. Reakční síly jsou síly vazbové. Při použití zobecněného principu virtuální práce nám tedy bude stačit uvažovat tíhovou sílu \(\vec{F_G}\), která působí proti směru osy y:
\[\vec{F_G}=(0,-mg).\]
Nápověda 2
Napište si zobecněný princip virtuální práce a uvědomte si, která virtuální posunutí potřebujete znát.
Řešení nápovědy 2
Zobecněný princip virtuální práce zní takto:
\[\sum_{i=1}^N \vec{F_i}\cdot\delta\vec{r_i}=0,\]
kde \(\vec{F_i}\) jsou výslednice vtištěných sil na i-tý hmotný bod a \(\vec{r_i}\) jsou virtuální posunutí slučitelná s vazbami i-tého hmotného bodu.

Vzhledem k tomu, že x-ová složka tíhové síly je nulová, nemusíme uvažovat člen, obsahující virtuální posunutí v tomto směru. Zobecněný princip virtuální práce tak bude mít pouze jeden člen:
\[F_y\delta y=0.\]
Nápověda 3
Abychom mohli určit virtuální posunutí \(\delta y\) slučitelné s vazbou, musíme nejprve znát vyjádření souřadnice y pomocí parametrů, které se mohou při zadané vazbě neomezeně měnit. Tím je v našem případě úhel ϑ, který určuje sklon tyče vzhledem k vodorovné rovině.

Vyjádřete souřadnici y pomocí úhlů α a β, které svírají roviny stěn s vodorovnou rovinou, délky tyče l a úhlu ϑ.
Nápověda 3a
Souřadnici y těžiště T vyjádříme jako součet vzdáleností o a w, kde o je vzdálenost těžiště a kolmého průmětu bodu A do osy rovnoběžné s osou y procházející těžištěm a w je vzdálenost bodu A od vodorovné roviny procházející počátkem soustavy souřadnic (viz obrázek).
Řešení nápovědy 3a
Vzdálenost o určíme z pravoúhlého trojúhelníka (označený na obrázku červeně), kde o je odvěsna, přepona má délku poloviny tyče a úhel protilehlý ke straně o je ϑ. Tedy:
\[o=\frac{1}{2}l\sin{\vartheta}.\tag{1}\]
Vzdálenost w určíme také z pravoúhlého trojúhelníka (označený na obrázku modře). Odvěsnou je w. Protilehlý úhel ke straně w má stejnou velikost jako úhel α (jedná se o střídavý úhel). Přepona v bude v našem trojúhelníku vzdálenost bodu A a počátku soustavy souřadnic (označme si jej jako O). Pro w tedy platí:
\[w=v\sin{\alpha}.\tag{2}\]
Zbývá určit vzdálenost v.
Nápověda 3b
Abychom získali vztah pro souřadnici těžiště y, chybí nám vyjádřit vzdálenost v. Tu lze nejrychleji vyjádřit použitím sinové věty v trojúhelníku ABO.
Řešení nápovědy 3b
V trojúhelníku ABO představuje strana AB délku tyče l a úhel při vrcholu O má velikost 180°− (α+β) (viz obrázek). Neznámou, kterou chceme ze sinové věty vyjádřit je strana AO, kterou jsme označili v. Zbývá tedy určit velikost úhlu při vrcholu B. Tu můžeme vyjádřit jako rozdíl β−ϑ. (Z obrázku je vidět, že výsledný úhel získáme, pokud odečteme od úhlu, který svírá strana BO s vodorovným směrem úhel, který svírá strana BA s vodorovným směrem. V obou případech se jedná o střídavé úhly k úhlu β, respektive ϑ.)

Sinovou větu tedy píšeme ve tvaru:
\[\frac{v}{\sin{(\beta-\vartheta)}}=\frac{l}{\sin{(180°-(\alpha+\beta))}}.\]
Pro jmenovatel zlomku na pravé straně rovnice platí:
\[\sin{(180°-(\alpha+\beta))}=\sin{(\alpha+\beta)}.\]
Hledanou neznámou v proto můžeme vyjádřit ve tvaru:
\[v=\frac{l\sin{(\beta-\vartheta)}}{\sin{(\alpha+\beta)}}.\tag{3}\]
Řešení nápovědy 3
Pro souřadnici y jsme v předchozích nápovědách odvodili vztah:
\[y=o+w.\]
Za o dosadíme z rovnice (1), za w pak postupně dosazujeme z rovnice (2) a (3). Získáváme tak vyjádření:
\[y=\frac{1}{2}l\sin{\vartheta}+\frac{l\sin{(\beta-\vartheta)}}{\sin(\alpha +\beta)}\sin{\alpha}.\]
Nápověda 4
Určete virtuální posunutí δy souřadnice y vzhledem k malé změně úhlu ϑ, který svírá tyč s vodorovnou rovinou.
Řešení nápovědy 4
Virtuální posunutí souřadnice y vzhledem k malé změně úhlu ϑ určíme jako:
\[\delta y=\frac{\mathrm{d}y}{\mathrm{d}\vartheta}\delta\vartheta.\]
Provedeme naznačenou derivaci a získáme:
\[\delta y=\left(\frac{1}{2}l\cos{\vartheta}-\frac{l\cos{(\beta-\vartheta)}}{\sin(\alpha +\beta)}\sin{\alpha}\right)\delta\vartheta.\]
Nápověda 5
Dosaďte za δy do rovnice vyjadřující zobecněný princip virtuální práce, kterou jsme napsali v řešení nápovědy 2 a odvoďte podmínku rovnováhy tyče mezi šikmými stěnami.
Goniometrické vzorce
Při výpočtu se nám budou hodit součtové vzorce pro goniometrické funkce.

Pro každá dvě reálná čísla x, y platí:
\[\sin{(x+y)}=\sin{x}\cos{y}+\cos{x}\sin{y},\] \[\sin{(x-y)}=\sin{x}\cos{y}-\cos{x}\sin{y},\] \[\cos{(x+y)}=\cos{x}\cos{y}-\sin{x}\sin{y},\] \[\cos{(x-y)}=\cos{x}\cos{y}+\sin{x}\sin{y}.\]
Řešení nápovědy 5
Dosazujeme do rovnice:
\[F_y\delta y=0.\]
Tedy:
\[-mg\left(\frac{1}{2}l\cos{\vartheta}-\frac{l\cos{(\beta-\vartheta)}}{\sin(\alpha +\beta)}\sin{\alpha}\right)\delta\vartheta=0.\]
Jelikož hmotnost m, gravitační zrychlení g, ani virtuální posunutí δϑ nejsou nulová, bude pravá strana nabývat nulové hodnoty právě tehdy, když bude závorka rovna nule:
\[\frac{1}{2}l\cos{\vartheta}-\frac{l\cos{(\beta-\vartheta)}}{\sin(\alpha +\beta)}\sin{\alpha}=0.\]
Nyní je zapotřebí vyjádřit neznámý úhel ϑ.

Celou rovnici můžeme vydělit nenulovou délkou tyče l. Rovnici upravíme tak, abychom se zbavili zlomků:
\[\cos{\vartheta}\sin{(\alpha+\beta)}=2\cos{(\beta-\vartheta)}\sin{\alpha}.\]
Použijeme součtové vzorce:
\[\cos{\vartheta}\sin{\alpha}\cos{\beta}+\cos{\vartheta}\cos{\alpha}\sin{\beta}=2\sin{\alpha}\cos{\beta}\cos{\vartheta}+2\sin{\alpha}\sin{\beta}\sin{\vartheta}.\]
Členy, kde se nachazí \(\cos{\vartheta}\), převedeme na levou stranu a členy, kde je \(\sin{\vartheta}\), necháme na pravé straně rovnice. Obě tyto funkce vytkneme a získáme:
\[\cos{\vartheta}\left(\sin{\alpha}\cos{\beta}+\cos{\alpha}\sin{\beta}-2\sin{\alpha}\cos{\beta}\right)=\sin{\vartheta}(2\sin{\alpha}\sin{\beta}).\]
Členy, kde se nachází neznámá ϑ, přesuneme na jednu stranu a po úpravě získáváme:
\[\mathrm{tg}\,\vartheta=\frac{1}{2}(\mathrm{cotg}\,\alpha-\mathrm{cotg}\,\beta).\]
Tento výraz již můžeme považovat za podmínku rovnováhy.
Celkové řešení
K řešení úlohy využijeme zobecněného principu virtuální práce:
\[\sum_{i=1}^N \vec{F_i}\cdot\delta\vec{r_i}=0,\]
kde \(\vec{F_i}\) jsou vtištěné síly a \(\vec{r_i}\) jsou k nim příslušná virtuální posunutí slučitelná s vazbami.

Na tyč působí vtištěná tíhová síla a vazbové reakční síly v místech dotyku tyče s rovinami. Stačí proto uvažovat tíhovou sílu, která působí proti směru osy y:
\[\vec{F}=(0,-mg).\]
Její působiště je v těžišti tyče.

Vzhledem k tomu, že x-ová složka síly je nulová, nemusíme uvažovat člen, obsahující tuto složku. Zobecněný princip virtuální práce tak bude mít pouze jeden člen:
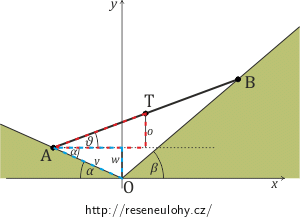
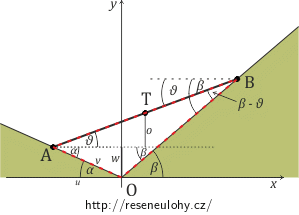
\[F_y\delta y=0.\]
Zbývá určit virtuální posunutí \(\delta y\) tak, aby bylo slučitelné s vazbami. K tomu je vhodné vyjádřit souřadnici y těžiště T tyče pomocí úhlů α a β, které svírají roviny stěn s vodorovnou rovinou, délky tyče l a úhlu ϑ, který určuje sklon tyče vzhledem k vodorovné rovině a který jako nezávislý parametr určuje polohu tyče. Na základě úvah o geometrii problému můžeme pro souřadnici y psát (podrobně viz nápověda 3):
\[y=\frac{1}{2}l\sin{\vartheta}+\frac{l\sin{(\beta-\vartheta)}}{\sin(\alpha +\beta)}\sin{\alpha}.\]
Virtuální posunutí souřadnice y vzhledem k úhlu ϑ je:
\[\delta y=\frac{\mathrm{d}y}{\mathrm{d}\vartheta}\delta\vartheta.\]
Provedeme naznačenou derivaci a získáváme:
\[\delta y=\left(\frac{1}{2}l\cos{\vartheta}-\frac{l\cos{(\beta-\vartheta)}}{\sin(\alpha +\beta)}\sin{\alpha}\right)\delta\vartheta.\]
Nyní již známe vše potřebené a můžeme dosadit do rovnice:
\[F_y\delta y=0.\]
Tedy:
\[-mg\left(\frac{1}{2}l\cos{\vartheta}-\frac{l\cos{(\beta-\vartheta)}}{\sin(\alpha +\beta)}\sin{\alpha}\right)\delta\vartheta=0.\]
Jelikož hmotnost m, gravitační zrychlení g, ani virtuální posunutí δϑ nejsou nulová, bude pravá strana nabývat nulové hodnoty právě tehdy, když bude závorka rovna nule. Získáváme proto:
\[\frac{1}{2}l\cos{\vartheta}-\frac{l\cos{(\beta-\vartheta)}}{\sin(\alpha +\beta)}\sin{\alpha}=0.\]
Z rovnice vyjádříme neznámou ϑ. Rozepsané úpravy spolu se vzorci, které jsou pro úpravy zapotřebí, naleznete v nápovědě 5. Získáváme tak podmínku rovnováhy tyče mezi dvěma stěnami:
\[\mathrm{tg}\,\vartheta=\frac{1}{2}(\mathrm{cotg}\,\alpha-\mathrm{cotg}\,\beta).\]
Odpověď
Pro úhel \( \vartheta \), který svírá za rovnováhy tyč s vodorovnou rovinou, platí:
\[\mathrm{tg}\,\vartheta=\frac{1}{2}(\mathrm{cotg}\,\alpha-\mathrm{cotg}\,\beta).\]
Komentář – speciální případy
Probereme si některé speciální případy volby úhlů α a β.

Tyč klouže po nakloněných rovinách bez tření. V případě, že by se např. úhel α rovnal nule, sjede tyč dolů a bude celou svou délkou nad (pro tuto volbu vodorovnou) rovinou.

Zkontrolujeme, zda náš výsledek odpovídá tomuto případu.

V řešení úlohy jsme dospěli k výsledku:
\[\mathrm{tg}\,\vartheta=\frac{1}{2}(\mathrm{cotg}\,\beta-\mathrm{cotg}\,\alpha).\]
Jelikož \(\mathrm{cotg}\,\alpha\) pro α = 0 není definován, pomůžeme si jiným vyjádřením, které naleznete v řešení nápovědy 5:
\[\cos{\vartheta}\sin{(\alpha+\beta)}=2\cos{(\beta-\vartheta)}\sin{\alpha}.\]
Dosadíme α = 0 a dostaneme:
\[\cos{\vartheta}\sin{\beta}=0.\]
Rovnice bude mít řešení buď \(\cos{\vartheta} = 0 \) nebo \(\sin{\beta}=0\).

Tedy pro úhly v intervalu (0,π] dostáváme, že ϑ=π/2, nebo β = 0.

Výsledek pro β = 0 odpovídá našemu předpokladu a získali jsme ještě další výsledek, kde ϑ = π/2 odpovídá případu, kdy by tyč „balancovala“ na jednom svém konci. V posledním zmiňovaném případě se jedná o labilní polohu.
Komentář 2 – speciální případy
Podívejme se, zda se zjednoduší řešení v případě, že roviny budou spolu svírat pravý úhel.

Řešení bude probíhat stejně až do nápovědy 3b, kde místo sinové věty, postačí Pythagorova věta. Vyjádření souřadnice y tak získáme v jednodušším tvaru:
\[y=\frac{1}{2}l\sin{\vartheta}+l\sin{(\beta-\vartheta)}\sin{\alpha}.\]
Obdobnými kroky jako v obecném řešení získáváme podmínku podmínku rovnováhy:
\[\frac{1}{2}\cos{\vartheta}-\cos{(\beta-\vartheta)}\sin{\alpha}=0.\]
Rovnici upravíme pomocí součtových vzorců na:
\[\cos{\vartheta}=2\sin{\alpha}\cos{\beta}\cos{\vartheta}+2\sin{\alpha}\sin{\beta}\sin{\vartheta}.\]
Pro α+β = 90° platí, že:
\[\sin{\alpha}=\cos{\beta},\] \[\cos{\alpha}=\sin{\beta}.\]
S využitím těchto vztahů můžeme rovnici upravit do tvaru:
\[\mathrm{tg}\,\vartheta=\frac{1}{\sin{2\alpha}}-\mathrm{tg}\,{\alpha}=\frac{1}{\sin{2\beta}}-\mathrm{cotg}\,{\beta}.\]