Sbírka řešených úloh

Kyvadlo ve vlaku – rovnovážná poloha

Úloha číslo: 937

• Nápověda 1

  Rozmyslete si, případně i prakticky vyzkoušejte, v jaké poloze se kyvadlo ustálí. Bude viset svisle dolů, nebo bude nějak vychýleno?

  Nakreslete si obrázek kyvadla ve vlaku a zaneste do něj síly, které na kyvadlo působí.

  Rozhodněte se, zda úlohu budete řešit z pohledu pozorovatele spjatého se zemí, nebo z pohledu pozorovatele jedoucího vlakem.

  Můžete zkusit řešit úlohu oběma přístupy.

• Řešení nápovědy 1 – pro pozorovatele spjatého se zemí

  V tomto případě řešíme úlohu v tzv. inerciální vztažné soustavě. Kyvadlo se vůči pozorovateli pohybuje se zrychlením \(\vec{a}\) a působí na něj dvě síly. Síla tíhová \(\vec{F_\mathrm{G}}\), která působí svisle dolů, a tahová síla závěsu \(\vec{F_\mathrm{z}}\), která působí ve směru závěsu.

  Výslednici těchto dvou sil označíme \(\vec{F}\). Jelikož je kyvadlo spojeno s vlakem, musí být výsledná síla \(\vec{F}\) úměrná zrychlení, se kterým se vlak (a tudíž i kyvadlo) pohybuje.

  Jak je vidět na obrázku, kyvadlo se ustálí v poloze vychýlené od svislého směru.

  

• Řešení nápovědy 1 – pro pozorovatele ve vlaku

  V tomto případě řešíme úlohu v tzv. neinerciálním systému. Kyvadlo je vůči pozorovateli v klidu. Tentokrát na něj působí tři síly. Síla tíhová \(\vec{F_\mathrm{G}}\), která působí svisle dolů, tahová síla závěsu \(\vec{F_\mathrm{z}}\), která působí ve směru závěsu, a setrvačná síla \(\vec{F_\mathrm{s}}\), která působí proti směru zrychlení vlaku. Výslednice těchto tří sil musí být nulová, protože vůči pozorovateli je kyvadlo v klidu.

  

• Nápověda 2

  Napište velikosti sil a z geometrie úlohy určete rovnovážnou polohu kyvadla v závislosti na úhlu α, který svírá závěs kyvadla se svislým směrem.

• Řešení nápovědy 2 – inerciální vztažná soustava

  Velikost tíhové síly \(\vec{F}_\mathrm{G}\) je:

  \[|\vec{F}_\mathrm{G}|=mg,\]

  kde m je hmotnost kyvadla a g tíhové zrychlení.

  Velikost výsledné síly známe. Kyvadlo je spojeno s vlakem a společně s ním se vzhledem k inerciálnímu pozorovateli pohybuje se zrychlením \(\vec{a}\). Velikost výsledné síly působící na kyvadlo získáme jako součin velikosti zrychlení a hmotnosti kyvadla. Tedy:

  \[|\vec{F}|=ma.\]

  Podmínku rovnováhy určíme z pravoúhlého trojúhelníka, který tyto síly svírají (viz obrázek v první nápovědě). Tedy:

  \[\mathrm{tg}\,\alpha=\frac{|\vec{F}|}{|\vec{F}_G|}=\frac{ma}{mg}=\frac{a}{g}.\]

• Řešení nápovědy 2 – neinerciální vztažná soustava

  Velikost tíhové síly \(\vec{F}_\mathrm{G}\) je:

  \[|\vec{F}_\mathrm{G}|=mg,\]

  kde m je hmotnost kyvadla a g tíhové zrychlení.

  Dále známe velikost setrvačné síly \(\vec{F}_\mathrm{s}\). Je úměrná zrychlení vlaku \(\vec{a}\):

  \[|\vec{F}_\mathrm{s}|=ma.\]

  Podmínku rovnováhy určíme z pravoúhlého trojúhelníka, který tyto síly svírají (viz obrázek v druhé nápovědě). Tedy:

  \[\mathrm{tg}\,\alpha=\frac{|\vec{F}_\mathrm{s}|}{|\vec{F}_\mathrm{G}|}=\frac{ma}{mg}=\frac{a}{g}.\]

• Celkové řešení

  Nejprve se rozhodneme, zda na úlohu pohlížíme z pohledu pozorovatele spjatého se zemí (inerciální vztažná soustava), nebo z pohledu pozorovatele jedoucího vlakem (neinerciální vztažná soustava).

  Nakreslíme si obrázek kyvadla ve vlaku a zaneseme příslušné síly.

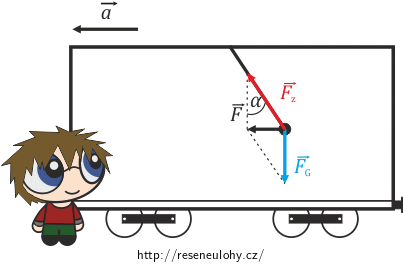
  Řešení z pohledu inerciální vztažné soustavy:

  

  Kyvadlo se vůči pozorovateli pohybuje se zrychlením \(\vec{a}\) a působí na něj dvě síly. Síla tíhová \(\vec{F_\mathrm{G}}\), která působí svisle dolů, a tahová síla závěsu \(\vec{F_\mathrm{z}}\), která působí ve směru závěsu.

  Výslednici těchto dvou sil označíme \(\vec{F}\). Jelikož je kyvadlo spojeno s vlakem, bude výsledná síla \(\vec{F}\) úměrná zrychlení, se kterým se vlak (a tudíž i kyvadlo) pohybuje.

  Velikost tíhové síly \(\vec{F}_\mathrm{G}\) je:

  \[|\vec{F}_\mathrm{G}|=mg,\]

  kde m je hmotnost kyvadla a g tíhové zrychlení.

  Velikost výsledné síly známe. Kyvadlo je spojeno s vlakem a společně s ním se vzhledem k inerciálnímu pozorovateli pohybuje se zrychlením \(\vec{a}\). Velikost výsledné síly působící na kyvadlo získáme jako součin velikosti zrychlení a hmotnosti kyvadla. Tedy:

  \[|\vec{F}|=ma.\]

  Podmínku rovnováhy určíme z pravoúhlého trojúhelníka, který tyto síly svírají (viz obrázek). Tedy:

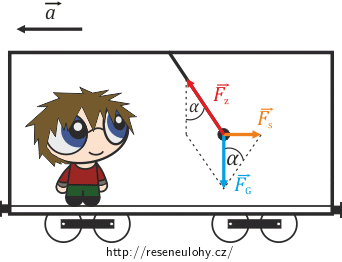
  \[\mathrm{tg}\,\alpha=\frac{|\vec{F}|}{|\vec{F}_\mathrm{G}|}=\frac{ma}{mg}=\frac{a}{g}.\]

  Řešení z pohledu neinerciální vztažné soustavy:

  

  Kyvadlo je vůči pozorovateli v klidu. Tentokrát na něj působí tři síly. Síla tíhová \(\vec{F_\mathrm{G}}\), která působí svisle dolů, tahová síla závěsu \(\vec{F_\mathrm{z}}\), která působí ve směru závěsu, a setrvačná síla \(\vec{F_\mathrm{s}}\), která působí proti směru zrychlení vlaku. Výslednice těchto tří sil musí být nulová, protože vůči pozorovateli je kyvadlo v klidu.

  Velikost tíhové síly \(\vec{F}_\mathrm{G}\) je:

  \[|\vec{F}_\mathrm{G}|=mg,\]

  kde m je hmotnost kyvadla a g tíhové zrychlení.

  Dále známe velikost setrvačné síly \(\vec{F}_\mathrm{s}\). Je úměrná zrychlení vlaku \(\vec{a}\):

  \[|\vec{F}_\mathrm{s}|=ma.\]

  Podmínku rovnováhy určíme z pravoúhlého trojúhelníka, který tyto síly svírají (viz obrázek). Tedy:

  \[\mathrm{tg}\,\alpha=\frac{|\vec{F}_\mathrm{s}|}{|\vec{F}_\mathrm{G}|}=\frac{ma}{mg}=\frac{a}{g}.\]

  Ze srovnání výsledků pro rovnovážnou polohu z pohledu inerciální a neinerciální soustavy vyplývá, že rovnovážná poloha nezávisí na volbě vztažné soustavy.

• Odpověď

  Kyvadlo ve vlaku, který se pohybuje se zrychlením \(\vec{a}\), je v rovnovážné poloze, pro kterou platí:

  \[\mathrm{tg}\,\alpha=\frac{a}{g},\]

  kde α je úhel, který svírá závěs kyvadla se svislým směrem, a g je tíhové zrychlení.