Sbírka řešených úloh

Pohyb okolo labilní rovnovážné polohy na kouli

Úloha číslo: 2263

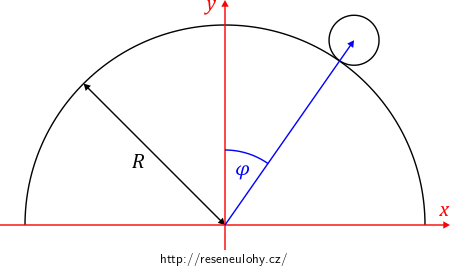
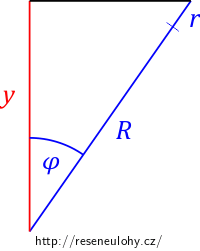
Mějme kuličku o hmotnosti \(m\) a poloměru \(r\), která se bez prokluzu pohybuje v blízkosti labilní rovnovážné polohy na kouli o poloměru \(R\).

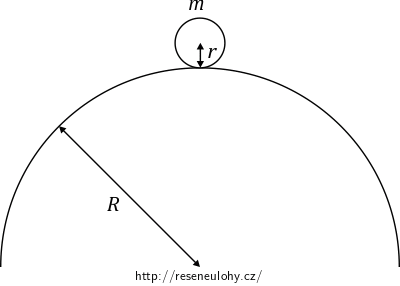
Pomocí aproximací pro malé kmity najděte pohybovou rovnici pro tuto kuličku.

• Nápověda

  Zvolte si soustavu souřadnic. Rozhodněte, kolik a jakých zobecněných souřadnic budete používat.

  Pro řešení pomocí Lagrangeových rovnic druhého druhu nebo pomocí Hamiltonových rovnic budete potřebovat znalost vztahu pro kinetickou a potenciální energii.

• Řešení – Nápověda

  Jedná se o problém s jedním stupněm volnosti, vystačíme si tedy s jednou zobecněnou souřadnicí. Za zobecněnou souřadnici zvolme odchylku \(\varphi\) od svislého směru.

  

  Kinetická energie \(T\) kuličky bude dána pohybem translačním a rotačním. K určení energie translačního pohybu potřebujeme znát rychlost kuličky v závislosti na \(\varphi\). Střed kuličky se pohybuje po kružnici o poloměru \(R + r\), tedy rychlost kuličky určíme ze známých vztahů pro pohyb po kružnici.

  \[v = \omega \left( R + r \right) = \dot{\varphi} \left( R + r \right)\] \[T_{translační} = \frac{1}{2} m v^2 = \frac{m}{2} \left( R + r \right)^2 \dot{\varphi}^2 \]

  K určení kinetické energie rotačního pohybu potřebujeme znát úhlovou rychlost \(\omega_k\) rotace kuličky kolem osy procházející jejím středem. Tu určíme díky předpokladu, že se kulička pohybuje bez prokluzu, tedy v čase \(t\) musí být délky uraženého oblouku na obou kružnicích stejné.

  \[R \dot{\varphi} t = r \omega_k t\] \[\frac{R}{r} \dot{\varphi} = \omega_k\]

  S touto znalostí už snadno určíme kinetickou energii rotačního pohybu jako:

  \[T_{rotační} = \frac{1}{2} J \omega_k^2 = \frac{J R^2}{2 r^2} \dot{\varphi}^2 \, .\]

  Celková kinetická energie je prostým součtem energií rotačního a translačního pohybu.

  \[T = \frac{J R^2}{2 r^2} \dot{\varphi}^2 + \frac{m}{2} \left( R + r \right)^2 \dot{\varphi}^2\] \[T = \left( \frac{J R^2}{2 r^2} + \frac{m \left( R + r \right)^2}{2} \right) \dot{\varphi}^2\] \[T = \frac{J R^2 + m r^2 \left( R + r \right)^2}{2 r^2} \dot{\varphi}^2\]

  Kinetickou energii \(T\) jsme určili, je na čase zaobírat se potenciální energií \(V\).

  Potenciální energie \(V\) homogenního gravitačního pole je:

  \[ V = m g y ,\]

  kde \(g\) je gravitační zrychlení. My ovšem potřebujeme mít potenciální energii \(V\) kuličky závislou na úhlu \(\varphi\). Potřebujeme tedy najít vztah mezi \(y\) a \(\varphi\). K tomu nám poslouží obrázek.

  

  Z obrázku vidíme, že:

  \[\cos \varphi = \frac{y}{R+r} \, .\] \[y = \left( R + r \right) \cos \varphi\]

  Potom lze potenciální energii \(V\) popsat následujícím vztahem.

  \[V = m g y = m g \left( R + r \right) \cos \varphi\]

  Přestože se nejedná o kmitání, jedná se o pohyb v okolí rovnovážné polohy a budeme chtít potenciální energii aproximovat kvadratickou funkcí \(\varphi\).

  Poznámka: Odůvodnění této aproximace viz např.: Studijní text k teoretické mechanice malých kmitů.

  Pro určení aproximace potenciální energie \(V\) použijeme Maclaurinovu formuli pro rozvoj funkce \(\cos x\).

  \[\cos x \approx 1 - \frac{x^2}{2!} + \frac{x^4}{4!}\]

  Jelikož uvažujeme malé výchylky, můžeme člen s \(x^4\) a ostatní členy zanedbat a potenciální energie potom bude:

  \[V \approx m g \left( R + r \right) \left( 1 - \frac{\varphi^2}{2} \right)\]

  Po této aproximaci budeme znát přibližný vztah pro naši potenciální energii \(V\).

  \[V = - \frac{m g \left( R + r \right)}{2}\varphi^2 + m g \left( R + r \right) = - \frac{m g \left( R + r \right)}{2}\varphi^2 - \mathrm{konst.}\]

  Známe tedy vztah pro kinetickou energii \(T\) i vztah pro potenciální energii \(V\) a umíme tak určit i lagrangián \(L = T - V\).

  \[L = \frac{J R^2 + m r^2 \left( R + r \right)^2}{2 r^2} \dot{\varphi}^2 + \frac{m g \left( R + r \right)}{2}\varphi^2 + \mathrm{konst.}\]

• Řešení – Lagrangeovy rovnice druhého druhu

  K nalezení pohybové rovnice užijeme Lagrangeových rovnic druhého druhu. Jelikož má náš problém pouze jeden stupeň volnosti, bude tato rovnice pouze jedna.

  \[\frac{\mathrm{d}}{\mathrm{d}t} \left( \frac{\partial L}{\partial \dot{\varphi}} \right) - \frac{\partial L}{\partial \varphi} = 0 \]

  Spočítejme postupně všechny nutné derivace našeho \(L\).

  \[L = \frac{J R^2 + m r^2 \left( R + r \right)^2}{2 r^2} \dot{\varphi}^2 + \frac{m g \left( R + r \right)}{2}\varphi^2 + \mathrm{konst.}\] \[\frac{\partial L}{\partial \varphi} = m g \left( R + r \right) \varphi \] \[\frac{\partial L}{\partial \dot{\varphi}} = \frac{J R^2 + m r^2 \left( R + r \right)^2}{r^2} \dot{\varphi}\] \[\frac{\mathrm{d}}{\mathrm{d}t} \left( \frac{\partial L}{\partial \dot{\varphi}} \right) = \frac{J R^2 + m r^2 \left( R + r \right)^2}{r^2} \ddot{\varphi}\]

  Potom tedy pro naši kuličku platí:

  \[\frac{\mathrm{d}}{\mathrm{d}t} \left( \frac{\partial L}{\partial \dot{x}} \right) - \frac{\partial L}{\partial x} = \frac{J R^2 + m r^2 \left( R + r \right)^2}{r^2} \ddot{\varphi} - m g \left( R + r \right) \varphi = 0 \, .\]

  Hledaná pohybová rovnice pro malé kmity má tvar:

  \[\ddot{\varphi} - \frac{m g r^2 \left( R + r \right)}{J R^2 + m r^2 \left( R + r \right)^2} \, \varphi = 0 \, .\]

  Jedná se o homogenní lineární diferenciální rovnici s konstantními koeficienty. Označíme-li \(\frac{m g r^2 \left( R + r \right)}{J R^2 + m r^2 \left( R + r \right)^2} = \omega^2\), pak lze obecné řešení zapsat ve tvaru:

  \[\varphi = A e^{\omega t} + B e^{ - \omega t}\, .\]

  K určení konstant \(A\) a \(B\) je nutné znát počáteční podmínky. Nechť je na začátku pohybu kulička na vrcholku větší koule, tedy \(\varphi_0 = \varphi (0) = 0\).

  \[\varphi (0) = A \, e^{\omega \cdot 0} + B \, e^{ - \omega \cdot 0} = A + B = 0\]

  Má-li nulovou i počáteční hybnost (tedy i rychlost), musí platit \(\dot \varphi (0) = 0\).

  \[\dot \varphi (0) = A \omega e^{\omega \cdot 0} - B \omega e^{ - \omega \cdot 0}\ = 0\] \[A - B = 0\] \[A = B\]

  Spojením s první počáteční podmínkou dostaneme \(2A = 2B = 0\), a tedy \(A = B = 0\). Řešení pohybové rovnice kuličky odpovídající počátečním podmínkám \(\varphi_0 = 0\) a \(\dot \varphi_0 = 0\) má tvar:

  \[\varphi = 0 \, .\]

  Tyto počáteční podmínky odpovídají tomu, že kulička je v klidu v labilní rovnovážné poloze a tedy se opravdu nikam nepohybuje.

• Řešení – Hamiltonovy rovnice

  Hamiltonovy kanonické rovnice připadají dvě na každý stupeň volnosti – rovnice pro změnu hybnosti \(\dot{p_i}\) a pro změnu zobecněné souřadnice \(\dot{q_i}\), v našem případě tedy budou pouze dvě:

  \[\dot{p} = - \frac{\partial H}{ \partial \varphi} \, ;\] \[\dot{\varphi} = \frac{\partial H}{\partial p},\]

  kde \(p\) je zobecněná hybnost a \(H(p,\varphi)\) je Hamiltonova funkce.

  Abychom pohybovou rovnici našli pomocí Hamiltonových rovnic, budeme potřebovat znát vztah pro zobecněnou hybnost kuličky.

  \[p = \frac{\partial L}{\partial \dot{\varphi}} = \frac{\partial}{\partial \dot{\varphi}} \left( \frac{J R^2 + m r^2 \left( R + r \right)^2}{2 r^2} \dot{\varphi}^2 + \frac{m g \left( R + r \right)}{2}\varphi^2 + \mathrm{konst.} \right) = \frac{J R^2 + m r^2 \left( R + r \right)^2}{r^2} \dot{\varphi}\]

  Nyní potřebujeme určit Hamiltonovu funkci \(H\). Pro \(H\) obecně platí vztah:

  \[H = \sum_{i=1}^N {p_i}{\dot{q_i}} - L \, .\]

  V našem případě se suma redukuje na jediný člen a výpočet nebude náročný.

  \[H = p \dot{\varphi} - L = \frac{J R^2 + m r^2 \left( R + r \right)^2}{r^2} \dot{\varphi}^2 - \frac{J R^2 + m r^2 \left( R + r \right)^2}{2 r^2} \dot{\varphi}^2 - \frac{m g \left( R + r \right)}{2}\varphi^2 - \mathrm{konst.} \] \[H = \frac{J R^2 + m r^2 \left( R + r \right)^2}{2 r^2} \dot{\varphi}^2 - \frac{m g \left( R + r \right)}{2}\varphi^2 - \mathrm{konst.} = T + V\] \[H = \frac{r^2}{J R^2 + m r^2 \left( R + r \right)^2} \frac{p^2}{2} - \frac{m g \left( R + r \right)}{2}\varphi^2 - \mathrm{konst.}\]

  Známe hamiltonián \(H\), tedy je načase dosadit do Hamiltonových kanonických rovnic.

  \[\dot{p} = - \frac{\partial H}{\partial \varphi} = m g \left( R + r \right) \varphi \] \[\dot{\varphi} = \frac{\partial H}{\partial p} = \frac{r^2}{J R^2 + m r^2 \left( R + r \right)^2} p\]

  Z druhé rovnice vyjádříme \(p\) a zderivujeme podle času, abychom získali \(\dot{p}\).

  \[p = \frac{J R^2 + m r^2 \left( R + r \right)^2}{r^2} \dot{\varphi} \, \, \, \, \big/ \frac{\partial}{\partial t}\] \[\dot{p} = \frac{J R^2 + m r^2 \left( R + r \right)^2}{r^2} \ddot{\varphi}\]

  Z druhé rovnice dosadíme do první za \(\dot{p}\).

  \[\frac{J R^2 + m r^2 \left( R + r \right)^2}{r^2} \ddot{\varphi} = \dot{p} = m g \left( R + r \right) \varphi\] \[\ddot{\varphi} - \frac{m g r^2 \left( R + r \right)}{J R^2 + m r^2 \left( R + r \right)^2} \, \varphi = 0 \]

  Toto je námi hledaná pohybová rovnice pro naši kuličku.

• Komentář – malinkatá kulička

  Pro kuličku nezanedbatelných rozměrů jsme pohybovou rovnici určili jako:

  \[\ddot{\varphi} - \frac{m g r^2 \left( R + r \right)}{J R^2 + m r^2 \left( R + r \right)^2} \, \varphi = 0 \, .\]

  Co kdyby byla kulička malinkatá, tedy měla zanedbatelné rozměry? Potom její moment setrvačnosti \(J\) je prakticky nulový a jelikož je \(R \gg r\), bude pohybová rovnice o kus jednodušší.

  \[\ddot{\varphi} - \frac{m g r^2 R}{m r^2 R^2} \, \varphi = 0\] \[\ddot{\varphi} - \frac{g}{R} \, \varphi = 0\]

  Takto by vypadala pohybová rovnice pro malé výchylky hmotného bodu sunoucího se z labilní rovnovážné polohy na vrcholku koule.

• Odpověď

  Při užití následující aproximace pro potenciální energii \(V\):

  \[V = - \frac{m g \left( R + r \right)}{2}\varphi^2 - \mathrm{konst.} \, ,\]

  má kulička pohybující se dle zadání pohybovou rovnici:

  \[\ddot{\varphi} - \frac{m g r^2 \left( R + r \right)}{J R^2 + m r^2 \left( R + r \right)^2} \, \varphi = 0 \, .\]