Sbírka řešených úloh

Kladka na pružině

Úloha číslo: 1188

Nalezněte pohybovou rovnici pro systém na obrázku, který se skládá z hmotné kladky zavěšené na pružině, přes níž je veden provaz držící závaží. Užijte Lagrangeových rovnic II. druhu.

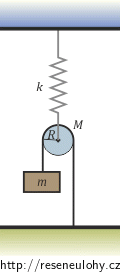
• Nápověda 1

  Rozmyslete si, kolik stupňů volnosti úloha má a kolik tedy bude třeba volit zobecněných souřadnic.

• Řešení nápovědy 1

  Úloha má jeden stupeň volnosti. Zadáme-li např. polohu kladky, bude už poloha závaží jednoznačně určena. Budeme tedy potřebovat pouze jednu zobecněnou souřadnici, pomocí které vyjádříme všechny potřebné geometrické závislosti.

• Nápověda 2

  Pro řešení úlohy pomocí Lagrangeových rovnic bude třeba najít lagrangián L, který se skládá z kinetické a potenciální energie. Vhodně zvolte souřadnicový systém a tyto energie vyjádřete. (Potenciální energie je dána až na konstantu. Volbu souřadnic proto proveďte tak, aby potenciální energie měla co nejpříjemnější tvar.)

• Řešení nápovědy 2 – volba souřadnic

  Systém se bude pohybovat pouze ve svislém směru. Osu x proto zvolíme svisle, její počátek zvolíme v rovnovážné poloze kladky a osa bude mířit směrem dolů.

  

  Z naší volby plyne, že okamžitá poloha kladky je rovna přímo souřadnici x a polohu závaží y můžeme vyjádřit jako:

  \[y=2x+c,\]

  kde c je konstanta, kterou lze určit z počátečních podmínek. Jedná se vlastně o vzdálenost kladky a závaží při rovnovážné poloze. Faktor 2 se u souřadnice x objeví proto, že pokud posuneme kladku o vzdálenost x, posune se závaží o dvojnásobnou vzdálenost.

  Ukažme si výhodu této volby počátku osy x. Pro další výpočty bude zapotřebí vyjádřit potenciální energii pružnosti pružiny V_p. Ta má obecně tvar:

  \[V_p=\frac{1}{2}k(x-x_0)^2,\]

  kde x₀ je souřadnice pro rovnovážnou polohu konce pružiny (= kladky) a x je její okamžitá poloha. Při naší volbě bude ale rovnovážná hodnota x₀ rovna nule a potenciální energie V_p bude tedy mít jednodušší tvar:

  \[V_p=\frac{1}{2}kx^2.\]

• Řešení nápovědy 2 – potenciální energie

  Potenciální energie V bude mít tři složky:

  • potenciální energie pružnosti pružiny V_p,
  • tíhová potenciální energie kladky V_M,
  • tíhová potenciální energie závaží V_m.

  Potenciální energii pružnosti V_p spočteme jako:

  \[V_p=\frac{1}{2}kx^2,\]

  kde k je tuhost pružiny a x okamžitá poloha konce pružiny = kladky (podrobněji viz předchozí oddíl).

  Tíhová potenciální energie kladky V_M o hmotnosti M má tvar:

  \[V_M=-Mgx.\]

  Znaménko mínus zde vyjadřuje skutečnost, že s narůstající souřadnicí x se potenciální energie zmenšuje.

  Tíhová potenciální energie závaží V_m o hmotnosti m má tvar:

  \[V_m=-mgy=-2mgx-mgc.\]

  Znaménko mínus je zde ze stejného důvodu jako výše.

  Celkovou potenciální energii systému tedy vyjádříme jako:

  \[V=V_p+V_M+V_m=\frac{1}{2}kx^2-Mgx-2mgx-mgc.\]

• Řešení nápovědy 2 – kinetická energie

  Celková kinetická energie systému T se skládá ze dvou složek, kinetické energie závaží a kinetické energie kladky. Kinetickou energii kladky vyjádříme podle Königovy věty jako součet energie posuvného a otáčivého pohybu. Celková kinetická energie má tedy tyto složky:

  • kinetickou energii posuvného pohybu kladky T_M,
  • kinetickou energii rotačního pohybu kladky T_r,
  • kinetickou energii posuvného pohybu závaží T_m.

  Kinetická energie posuvného pohybu kladky T_M o hmotnosti M má tvar:

  \[T_M=\frac{1}{2}M\dot{x}^2.\]

  Kinetická energie rotačního pohybu kladky T_r o momentu setrvačnosti J točící se úhlovou rychlostí ω je:

  \[T_r=\frac{1}{2}J\omega ^2,\]

  kde je vhodné převést úhlovou rychlost ω na vyjádření obsahující obvodovou rychlost, v našem případě \(\dot{x}\):

  \[\omega=\frac{\dot{x}}{R}.\]

  Kinetickou energii posuvného pohybu závaží T_m o hmotnosti m vyjádříme takto:

  \[T_m=\frac{1}{2}m\dot{y}^2=\frac{1}{2}m(2\dot{x})^2.\]

  Pro celkovou kinetickou energii platí:

  \[T=T_M+T_{r}+T_m=\frac{1}{2}M\dot{x}^2+\frac{1}{2}J\omega ^2+\frac{1}{2}m(2\dot{x})^2.\]

  Pro úpravu rovnice využijeme vztah pro moment setrvačnosti J kruhové desky o hmotnosti M a poloměru R, která se otáčí kolem osy procházející kolmo jejím středem (viz např. úloha 556):

  \[J=\frac{1}{2}MR^2.\]

  Po dosazení do rovnice pro celkovou kinetickou energii tak získáme:

  \[T=\frac{1}{2}M\dot{x}^2+\frac{1}{4}M\dot{x}^2+2m\dot{x}^2=\frac{3}{4}M\dot{x}^2+2m\dot{x}^2.\]

• Řešení nápovědy 2 – lagrangián

  Do vyjádření lagrangiánu dosadíme za kinetickou a potenciální energii:

  \[L=T-V=\frac{3}{4}M\dot{x}^2+2m\dot{x}^2-\frac{1}{2}kx^2+Mgx+2mgx+mgc.\]

• Nápověda 3

  Z teorie víme, že Lagrangeova rovnice pro úlohu s jedním stupněm volnosti má tvar:

  \[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial{L}}{\partial{\dot{x}}}\right)-\frac{\partial{L}}{\partial{x}}=0,\]

  kde x je zobecněná souřadnice a \(\dot{x}\) je zobecněná rychlost.

  Z předchozí nápovědy známe lagrangián L. Proveďte naznačené derivace a do rovnice dosaďte.

• Řešení nápovědy 3

  V nápovědě 2 jsme získali lagrangián ve tvaru:

  \[L=\frac{3}{4}M\dot{x}^2+2m\dot{x}^2-\frac{1}{2}kx^2+Mgx+2mgx+mgc.\]

  Nejprve spočteme parciální derivace lagrangiánu podle zobecněné souřadnice a rychlosti:

  \[\frac{\partial{L}}{\partial{x}}=-kx+Mg+2mg,\] \[\frac{\partial{L}}{\partial{\dot{x}}}=\frac{3}{2}M\dot{x}+4m\dot{x}.\]

  Poslední rovnost zderivujeme podle času a získáme:

  \[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial{L}}{\partial{\dot{x}}}\right)=\frac{3}{2}M\ddot{x}+4m\ddot{x}.\]

  Nyní již stačí dát obě části rovnice dohromady a sestavit tak Lagrangeovu rovnici II. druhu pro zkoumaný systém.

  \[\frac{3}{2}M\ddot{x}+4m\ddot{x}+kx-Mg-2mg=0.\]

  Rovnici upravíme a získáme tak konečný tvar:

  \[\ddot{x}+\frac{k}{4m+\frac{3}{2}M}x=\frac{2m+M}{4m+\frac{3}{2}M}g.\]

• Celkové řešení

  I když se systém skládá ze závaží a kladky, má pouze jediný stupeň volnosti, proto k jeho popisu budeme potřebovat pouze jednu zobecněnou souřadnici. Nejprve zvolíme soustavu souřadnic. Systém se bude pohybovat pouze ve svislém směru, proto v tomto směru zvolíme osu x a její počátek zvolíme v místě rovnovážné polohy kladky.

  

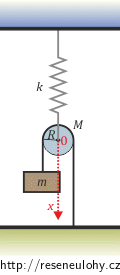
  Napíšeme vyjádření kinetické a potenciální energie systému. (Podrobnou diskusi naleznete v nápovědě 2.)

  \[T=\frac{3}{4}M\dot{x}^2+2m\dot{x}^2,\] \[V=\frac{1}{2}kx^2-Mgx-2mgx-mgc.\]

  Energie dosadíme do vyjádření lagrangiánu L:

  \[L=T-V=\frac{3}{4}M\dot{x}^2+2m\dot{x}^2-\frac{1}{2}kx^2+Mgx+2mgx+mgc.\]

  Lagrangián dosadíme do Lagrangeovy rovnice II. druhu, která má pro jeden stupeň volnost tvar:

  \[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial{L}}{\partial{\dot{x}}}\right)-\frac{\partial{L}}{\partial{x}}=0,\]

  kde x je zobecněná souřadnice a \(\dot{x}\) je zobecněná rychlost.

  Provedeme naznačené početní úkony a po úpravě získáváme hledanou pohybovou rovnici:

  \[\ddot{x}+\frac{k}{4m+\frac{3}{2}M}x=\frac{2m+M}{4m+\frac{3}{2}M}g.\]

  (Podrobný výpočet naleznete v nápovědě 3.)

• Odpověď

  Pohybová rovnice pro zkoumaný systém má tvar:

  \[\ddot{x}+\frac{k}{4m+\frac{3}{2}M}x=\frac{2m+M}{4m+\frac{3}{2}M}g,\]

  kde k je tuhost pružiny, M hmotnost kladky, m hmotnost závaží a g je tíhové zrychlení.

• Komentář – řešení pohybové rovnice

  V řešení úlohy jsme dospěli k nehomogenní lineární diferenciální rovnici 2. řádu s konstantními koeficienty ve tvaru:

  \[\ddot{x}+\frac{k}{4m+\frac{3}{2}M}x=\frac{2m+M}{4m+\frac{3}{2}M}g.\]

  Zlomek \(\frac{k}{4m+\frac{3}{2}M}\) označíme jako \(\omega ^2\). Celkové řešení rovnice tohoto typu je vhodné hledat ve tvaru:

  \[x=\tilde{x}+x_p,\]

  kde \(\tilde{x}\) je obecné řešení homogenní rovnice (rovnice s nulovou pravou stranou) a x_p je tzv. partikulární řešení, tj. jedno řešení celé rovnice.

  Začneme tedy s \(\tilde{x}\), homogenní rovnici dostáváme ve tvaru:

  \[\ddot{x}+\omega ^2x=0.\]

  Řešení této rovnice má tvar:

  \[\tilde{x}=Ke^{\lambda t},\]

  po dosazení do homogenní rovnice dostáváme tzv. charakteristickou rovnici pro neznámou konstantu λ:

  \[\ddot{\lambda}+\omega ^2\lambda=0,\]

  která má dvě řešení:

  \[\lambda=\pm i\omega.\]

  Z teorie lineárních diferenciáních rovnic víme, že pokud má rovnice více řešení, je řešením i každá lineární kombinace těchto řešení, řešení tvoří vektorový prostor. Tedy v našem případě:

  \[\tilde{x}=Ae^{i\omega t}+Be^{-i\omega t},\]

  kde A a B jsou libovolné komplexní konstanty. Uvedený tvar řešení může být obecně komplexní, my ale chceme najít řešení reálná, tj. ta s fyzikálním významem. Použijeme Eulerův vzorec pro komplexní exponenciálu a řešení rozepíšeme ve tvaru:

  \[\tilde{x}=A\cos{(\omega t)}+iA\sin{(\omega t)}+B\cos{(\omega t)}-iB\sin{(\omega t)}.\]

  Sloučíme členy u stejných goniometrických funkcí:

  \[\tilde{x}=(A+B)\cos{(\omega t)}+i(A-B)\sin{(\omega t)}.\]

  Konstanty A+B a A−B ale mohou být stále komplexní čísla, rozepíšeme je pomocí komplexní a reálné části:

  \[A+B=C+iD,\] \[A-B=E+iF,\]

  rovnici tedy píšeme ve tvaru:

  \[\tilde{x}=(C+iD)\cos{(\omega t)}+i(E+iF)\sin{(\omega t)},\]

  kde C, D, E a F jsou reálné konstanty.

  Získali jsme celý prostor komplexních řešení. Fyzikálně realizovatelná jsou pouze ta řešení, která jsou reálná:

  \[\tilde{x}=C\cos{(\omega t)}-F\sin{(\omega t)}.\]

  Nyní se zaměříme na partikulární řešení x_p. Snažíme se najít jedno řešení celé rovnice, zkusme tedy tu nejjednodušší možnost – x_p je konstanta vhodné velikosti. Jelikož konstanta při derivování vypadne, nabývá rovnice pro partikulární řešení tvar:

  \[\frac{k}{4m+\frac{3}{2}M}x_p=\frac{2m+M}{4m+\frac{3}{2}M}g.\]

  Pro x_p tedy dostáváme:

  \[x_p=\frac{(2m+M)g}{k}.\]

  Celé obecné řešení pohybové rovnice tak získáváme ve tvaru:

  \[x=\tilde{x}+x_p=C\cos{(\omega t)}-F\sin{(\omega t)}+\frac{(2m+M)g}{k}.\]

  Ještě je třeba určit konstanty C a F. To uděláme z počátečních podmínek. Označme počáteční polohu kladky x₀ a její rychlost v₀. Pro počáteční výchylku x₀ dosazením t = 0 dostáváme:

  \[x_0=C+\frac{(2m+M)g}{k},\]

  konstanta C má proto vyjádření:

  \[C=x_0-\frac{(2m+M)g}{k}.\]

  Konstantu F určíme pomocí počáteční rychlosti v₀. Musíme tedy nejprve zderivovat rovnici pro výchylku x podle času t a získat tak vyjádření rychlosti v:

  \[v=-C\omega\sin{(\omega t)}-F\omega\cos{(\omega t)},\]

  kam dosadíme t = 0 a dostaneme:

  \[v_0=-F\omega,\]

  tedy:

  \[F=-\frac{v_0}{\omega}.\]

  Celkové řešení pohybové rovnice pro polohu kladky x jsme získali ve tvaru:

  \[x=\left(x_0-\frac{(2m+M)g}{k}\right)\cos{(\omega t)}+\frac{v_0}{\omega}\sin{(\omega t)}+\frac{(2m+M)g}{k}.\]

  Kladka bude konat kmitavý pohyb daný touto rovnicí. Frekvence f tohoto kmitání má velikost:

  \[f=\frac{1}{2\pi}\sqrt{\frac{k}{4m+\frac{3}{2}M}}.\]

  Závaží bude kmitat se stejnou frekvencí, ale jeho výchylky budou dvojnásobné.