Hmotná kladka
Úloha číslo: 1237
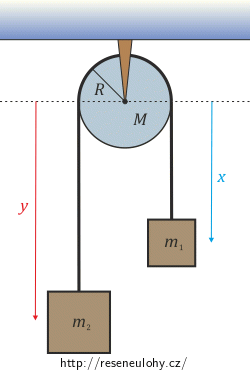
Na kladce visí dvě závaží o hmotnostech m1 a m2 (viz obrázek). Napište Lagrangeovu funkci, Lagrangeovy rovnice II. druhu, zobecněnou hybnost, Hamiltonovu funkci a Hamiltonovy kanonické rovnice pro případ:
- nehmotné kladky
- kladky, kterou tvoří homogenní disk o poloměru R a hmotnosti M
V obou případech nalezněte i zrychlení závaží.
Jako zobecněnou souřadnici x použijte vzdálenost prvního závaží od kladky.
a) Nápověda 1 – Lagrangeova funkce
Napište kinetickou a potenciální energii systému. Uvědomte si, že kladka je nehmotná, proto nemusíme počítat příspěvky kinetické energie plynoucí z jejího otáčení. Sestavte Lagrangeovu funkci.
a) Nápověda 2 – Lagrangeova rovnice
Z teorie víme, že Lagrangeova rovnice pro úlohu s jedním stupněm volnosti má tvar:
\[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial{L}}{\partial{\dot{x}}}\right)-\frac{\partial{L}}{\partial{x}}=0,\]kde x je zobecněná souřadnice a \(\dot{x}\) je zobecněná rychlost.
Z předchozí nápovědy známe lagrangián L. Proveďte naznačené derivace a do rovnice dosaďte.
a) Nápověda 3 – zobecněná hybnost
Vyjádřete zobecněnou hybnost p. Spočtěte ji pomocí Lagrangeovy funkce L podle vzorce:
\[p=\frac{\partial{L}}{\partial{\dot{q}}}.\]a) Nápověda 4
Sestavte Hamiltonovu funkci a napište Hamiltonovy kanonické rovnice. Při sestavování Hamiltonovy funkce je dobré si uvědomit, že lagrangián není explicitně závislý na čase.
b) Hmotná kladka
Pokud budeme uvažovat hmotnou kladku, potenciální energie zůstane stejná, protože kladka nemění svoji polohu. Změní se pouze kinetická energie, kde bude navíc člen Tk odpovídající otáčení hmotné kladky:
\[T_k=\frac{1}{2}J\omega ^2.\]Převedeme úhlovou rychlost ω na vyjádření obsahující obvodovou rychlost, v našem případě \(\dot{x}\):
\[T_k=\frac{1}{2}J\frac{\dot{x}^2}{R^2}.\]Použijeme vztah pro moment setrvačnosti J kladky:
\[J=\frac{1}{2}MR^2\]a po úpravě dostáváme:
\[T_k=\frac{1}{4}M\dot{x}^2.\]Lagrangián v takovém případě bude mít tvar:
\[L=\frac{1}{2}(m_1+m_2+\frac{1}{2}M)\dot{x}^2+m_1gx-m_2gx-K.\]Pomocí lagrangiánu můžeme sestavit Lagrangeovu rovnici II. druhu ve tvaru:
\[(m_1+m_2+\frac{1}{2}M)\ddot{x}-m_1g+m_2g=0\]a z ní vyplývá zrychlení:
\[\ddot{x}=\frac{m_1-m_2}{m_1+m_2+\frac{1}{2}M}g.\]Stejně jako u nehmotné kladky jsme získali výraz, který závisí na hmotnostech a gravitačním zrychlení. Ve jmenovateli přibyla hmotnost kladky M, která tak zrychlení brzdí. Pro M = 0 získáváme stejný vzorec jako v řešení nehmotné kladky.
Abychom mohli vyjádřit Hamiltonovu funkci v přirozených proměnných, potřebujeme znát zobeněnou hybnost p:
\[p=\frac{\partial{L}}{\partial{\dot{x}}}=\frac{\partial{\left(\frac{1}{2}(m_1+m_2+\frac{1}{2}M)\dot{x}^2+m_1gx-m_2gx-K\right)}}{\partial{\dot{x}}}=(m_1+m_2+\frac{1}{2}M)\dot{x}^2.\]Lagrangián nezávisí explicitně na čase, proto můžeme hamiltonián vyjádřit jako celkovou mechanickou energii:
\[H=T+V=\frac{1}{2}(m_1+m_2)\dot{x}^2+\frac{1}{4}M\dot{x}^2-m_1gx+m_2gx+K\]a zobecněnou rychlost vyjádříme pomocí zobecněné hybnosti:
\[H=\frac{p^2}{2m_1+2m_2+M}-m_1gx+m_2gx+K.\]Hamiltonovy rovnice tak mají tvar:
\[\dot{x}=\frac{p}{m_1+m_2+\frac{1}{2}M},\] \[\dot{p}=m_1g-m_2g.\]Pomocí těchto rovnic již můžeme vyjádřit zrychlení systému jako:
\[\ddot{x}=\frac{m_1-m_2}{m_1+m_2+\frac{1}{2}M}g.\]Všimněte si, že zrychlení vyšlo stejně jako pomocí Lagrangeových rovnic II. druhu.
Celkové řešení
Celkové řešení provedeme narozdíl od nápověd nejprve pro hmotnou kladku. Řešení pro nehmotnou kladku z něj získáte volbou:
\[M=0.\]Abychom mohli napsat Lagrangeovu funkci L, musíme znát vyjádření kinetické a potenciální energie. Pro potenciální energii platí:
\[V=V_1+V_2=-m_1gx-m_2gy+C.\]První člen odpovídá potenciální energií prvního závaží a druhý člen druhého závaží. Hmotná kladka nemění svoji polohu, proto jsme její potenciální energii označili jako C.
Souřadnici y můžeme vyjádřit pomocí délky provazu l jako:
\[y=l-\pi R-x.\]Dále se nám bude hodit vyjádření časové derivace souřadnice y.
\[\dot{y}=\frac{\mathrm{d}}{\mathrm{d}t}(l-\pi R-x)=-\dot{x}.\]Do vztahu pro potenciální energii dosadíme za y a dostáváme:
\[V=-m_1gx-m_2g(l-\pi R-x)+C.\]Potenciální energie systému je určena až na konstantu, proto bychom nemuseli konstantní členy uvažovat. Aby se tato skutečnost ukázala, ponechme konstatní členy ve výrazu pro potenciální energii, ale označme je dohromady jako K:
\[V=-m_1gx+m_2gx+K.\]Kinetická energie má tři složky, a to kinetickou energii posuvného pohybu T1 závaží o hmotnosti m1, kinetickou energii posuvného pohybu T2 závaží o hmotnosti m2 a kinetickou energii rotačního pohybu kladky Tk o hmotnosti M a poloměru R:
\[T=T_1+T_2+T_k=\frac{1}{2}m_1\dot{x}^2+\frac{1}{2}m_2\dot{y}^2+\frac{1}{2}J\omega ^2,\]převedeme úhlovou rychlost ω na vyjádření obsahující obvodovou rychlost, v našem případě \(\dot{x}\):
\[T=\frac{1}{2}m_1\dot{x}^2+\frac{1}{2}m_2\dot{(-x)}^2+\frac{1}{2}J\frac{\dot{x}^2}{R^2},\]použijeme vztah pro moment setrvačnosti J kladky:
\[J=\frac{1}{2}MR^2\]a po úpravě dostáváme:
\[T=\frac{1}{2}(m_1+m_2)\dot{x}^2+\frac{1}{4}M\dot{x}^2.\]Můžeme tedy napsat Lagrangeovu funkci:
\[L=T-V=\frac{1}{2}(m_1+m_2+\frac{1}{2}M)\dot{x}^2+m_1gx-m_2gx-K.\]Lagrangeova rovnice pro úlohu s jedním stupněm volnosti má tvar:
\[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial{L}}{\partial{\dot{x}}}\right)-\frac{\partial{L}}{\partial{x}}=0,\]kde x je zobecněná souřadnice a \(\dot{x}\) je zobecněná rychlost.
Spočteme parciální derivace lagrangiánu podle zobecněné souřadnice a rychlosti:
\[\frac{\partial{L}}{\partial{x}}=m_1g-m_2g,\] \[\frac{\partial{L}}{\partial{\dot{x}}}=(m_1+m_2+\frac{1}{2})M\dot{x}.\]Poslední rovnost zderivujeme podle času a získáme:
\[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial{L}}{\partial{\dot{x}}}\right)=(m_1+m_2+\frac{1}{2}M)\ddot{x}.\]Nyní již stačí dát obě části rovnice dohromady a sestavit tak Lagrangeovu rovnici II. druhu pro zkoumaný systém.
\[(m_1+m_2+\frac{1}{2}M)\ddot{x}-m_1g+m_2g=0.\]Hodnota konstanty K z potencilní energie se do pohybové rovnice nepromítla, proto ji skutečně nebylo třeba uvažovat.
Ještě vyjádříme celkové zrychlení:
\[\ddot{x}=\frac{m_1-m_2}{m_1+m_2+\frac{1}{2}M}g.\]Stejně jako u nehmotné kladky jsme získali výraz, který závisí na hmotnostech a gravitačním zrychlení. Ve jmenovateli přibyla hmotnost kladky M, která tak zrychlení brzdí. Pro M = 0 získáváme stejný vzorec jako v řešení nehmotné kladky.
Tím jsme dokončili řešení pomocí Lagrangeova formalismu a můžeme se pustit do řešení podle Hamiltonova.
Zobecněnou hybnost p můžeme spočítat podle vzorce:
\[p=\frac{\partial{L}}{\partial{\dot{q}}}.\]Provedeme naznačenou parciální derivaci a získáváme:
\[p=\frac{\partial{L}}{\partial{\dot{x}}}=\frac{\partial{\left(\frac{1}{2}m_1\dot{x}^2+\frac{1}{2}m_2\dot{x}^2+\frac{1}{4}M\dot{x}^2+m_1gx-m_2gx-K\right)}}{\partial{\dot{x}}}=m_1\dot{x}+m_2\dot{x}+\frac{1}{2}M\dot{x}=(m_1+m_2+\frac{1}{2}M)\dot{x}.\]Jelikož Lagrangeova funkce L není závislá na čase, můžeme Hamiltonovu funkci H snadno napsat jako celkovou mechanickou energii:
\[H=T+V=\frac{1}{2}(m_1+m_2+\frac{1}{4}M)\dot{x}^2-m_1gx+m_2gx+K.\]Přirozené proměnné hamiltoniánu jsou zobecněné souřadnice a hybnosti, proto výsledek ještě upravíme tak, aby v něm nevystupovala zobecněná rychlost \(\dot{x}\), ale zobecněná hybnost p:
\[H=\frac{p^2}{2m_1+2m_2+M}-m_1gx+m_2gx+K.\]Hamiltonovy kanonické rovnice mají obecně tvar:
\[\dot{q_i}=\frac{\partial{H}}{\partial{p_i}},\] \[\dot{p_i}=-\frac{\partial{H}}{\partial{q_i}}.\]V našem případě máme jedinou souřanici x a hybnost p. Rovnice tedy nabývají tvaru:
\[\dot{x}=\frac{\partial{H}}{\partial{p}},\] \[\dot{p}=-\frac{\partial{H}}{\partial{x}}.\]Dosadíme a provedeme naznačené derivace:
\[\dot{x}=\frac{p}{m_1+m_2+\frac{1}{2}M}.\] \[\dot{p}=m_1g-m_2g.\]První rovnici zderivujeme, tím přímo dostaneme vyjádření zrychlení, do kterého dosadíme druhou rovnici:
\[\ddot{x}=\frac{m_1-m_2}{m_1+m_2+\frac{1}{2}M}g.\]Všimněte si, že zrychlení vyšlo stejně jako pomocí Lagrangeových rovnic II. druhu.
Odpověď
Lagrangeova funkce pro systém s hmotnou kladkou má tvar:
\[L=\frac{1}{2}(m_1+m_2)\dot{x}^2+\frac{1}{4}M\dot{x}^2+m_1gx-m_2gx-K.\]Lagrangeovy rovnice II. druhu nabývají tvaru:
\[(m_1+m_2)\ddot{x}+\frac{1}{2}M\ddot{x}-m_1g+m_2g=0.\]Zobecněná hybnost má tvar:
\[p=(m_1+m_2)\dot{x}+\frac{1}{2}M\dot{x}.\]Hamiltonovu funkci jsme odvodili jako:
\[H=\frac{p^2}{2m_1+2m_2+M}-m_1gx+m_2gx+K.\]Hamiltonovy kanonické rovnice jsme získali jako:
\[\dot{x}=\frac{p}{m_1+m_2+\frac{1}{2}M}.\] \[\dot{p}=m_1g-m_2g.\]Zrychlení záváží jsme vypočítali jako:
\[\ddot{x}=\frac{m_1-m_2}{m_1+m_2+\frac{1}{2}M}g.\]Řešení pro nehmotnou kladku dostaneme dosazením M = 0.


