Tenký disk – hledání hlavních os setrvačnosti

Úloha číslo: 2248

Mějme velmi tenký homogenní disk hmotnosti \(M\) o poloměru \(R\) v rovině \(xy\). Osa \(z\) míří ven z nákresny.

Máme záváží hmotnosti \(m = \frac{M}{4}\) připevněno k okraji disku tak, jak je zobrazeno na obrázku.

Obrázek 1 – nákres disku s hmotným bodem

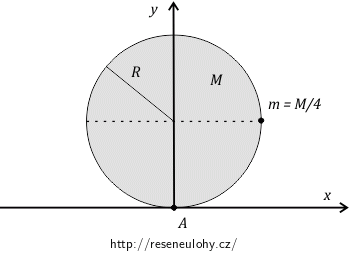
Najděte:

(A) tenzor setrvačnosti samotného disku vzhledem k jeho hmotnému středu,

(B) tenzor setrvačnosti samotného disku vzhledem k bodu \(A\),

(D) hlavní osy tenzoru setrvačnosti celého systému vzhledem k bodu \(A\).

Řešení – Úloha (A)
Toto zadání je již vyřešeno v úloze Tenzor setrvačnosti tenkého disku.
Nápověda (B)
Připoměňte si, co říká Steinerova věta.

Tuto větu aplikujte.
Řešení – Nápověda (B)

Steinerova věta

Známe-li moment setrvačnosti \(J_o\) tělesa vzhledem k ose \(o\) procházející jeho těžištěm, pak pro moment setrvačnosti \(J_d\) tohoto tělesa vzhledem k ose \(d\), která je rovnoběžná s osou \(o\) platí vztah:
\[J_d = J_o + m r^2 ,\]
kde \(m\) je hmotnost tělesa a \(r\) je vzdálenost os \(o\) a \(d\).

Podívejme se znovu na naši situaci.

Souřadnice s počátkem v těžišti disku jsme označili čárkovaně (\('\)). Momenty setrvačnosti vzhledem k čárkované soustavě jsme si spočítali v úloze (A).

Vidíme, že čárkovaná soustava souřadnic je posunutím nečárkované ve směru osy \(y\) o vzdálenost \(R\). To znamená, že osa \(y\) splývá s osou \(y'\). Dále navíc platí, že osa \(x\) je rovnoběžná s \(x'\) a osa \(z\) je rovnoběžná s \(z'\).

Aplikujme na naši situaci Steinerovu větu a začněme se složkou \(J_{yy}\). To nebude příliš náročné, protože vzdálenost os \(y\) a \(y'\) je nula a tedy dle Steinerovy věty (a také intuitivně):
\[J_{yy}=J_{y'y'} = \frac{M R^2}{4} .\]
Nyní spočítejme \(J_{xx}\). Vzdálenost os \(x\) a \(x'\) je \(R\).
\[J_{xx} = J_{x'x'} + M R^2 = \frac{M R^2}{4} + M R^2 = \frac{5 M R^2}{4}\]
Už nám zbývá určit jen \(J_{zz}\). Vzdálenost os \(z\) a \(z'\) je taktéž \(R\).
\[J_{zz} = J_{z'z'} + M R^2 = \frac{M R^2}{2} + M R^2 = \frac{3 M R^2}{2}\]
Zabývejme se dále deviačními momenty. Začneme složkami tenzoru \(J_{xz}\) a \(J_{yz}\).
\[J_{xz} = - \sigma \int_S xz \, \mathrm d S = - \sigma \int_S x \cdot 0 \, \mathrm d S = 0\] \[J_{yz} = - \sigma \int_S yz \, \mathrm d S = - \sigma \int_S y \cdot 0 \, \mathrm d S = 0\]
Tyto výpočty se ukázaly velmi jednoduché, protože se v nich přímo vyskytuje \(z = 0\). Pomocí parametrizace disku v nečárkovaných souřadnicích se dá ukázat, že také \(J_{xy}\) je rovno nule, zde se ovšem omezíme na prosté konstatování, že to tak je.

Zapišme tedy tenzor setrvačnosti disku vzhledem k bodu A do matice.
\[J_M = \begin{pmatrix} \frac {5 M R^2}{4} & 0 & 0 \\ 0 & \frac {M R^2}{4} & 0 \\ 0 & 0 & \frac {3 M R^2}{2} \end{pmatrix} = \frac {M R^2}{4} \begin{pmatrix} 5 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 6 \end{pmatrix} \]
Poznámka k úloze (B)
K vyřešení úlohy (B) jsme mohli použít i jiné věty.

„Věta o kolmé ose“

Věta o kolmé ose říká, že pokud leží ploché těleso úplně v rovině \(xy\), a známe momenty setrvačnosti \(J_x\) a \(J_y\), potom pro moment setrvačnosti \(J_z\) rotace okolo osy \(z\) kolmé k rovině \(xy\), přičemž se všechny tři osy rotace setkávají v jednom bodě, platí:
\[ J_z = J_x + J_y .\]
Ukažme ve stručnosti, že toto tvrzení opravdu platí.
\[J_x = \int_S {y^2 + z^2} \sigma \, \mathrm{d}S = \int_S y^2 \sigma \, \mathrm{d}S\] \[J_y = \int_S {x^2 + z^2} \sigma \, \mathrm{d}S = \int_S x^2 \sigma \, \mathrm{d}S\] \[J_z = \int_S {x^2 + y^2} \sigma \, \mathrm{d}S = \int_S x^2 \sigma \, \mathrm{d}S + \int_S y^2 \sigma \, \mathrm{d}S = J_x + J_y\]

Vidíme, že tímto jsme si mohli poněkud zjednodušit úlohu (A), kde by platilo, že \(J_{zz(A)} = 2 J_{xx(A)}\).

Také jsme mohli pomocí Steinerovy věty určit pouze \(J_{xx}\) a \(J_{yy}\), poté bychom už \(J_{zz}\) určili pouhým součtem.
Řešení – Úloha (B)
K vyřešení tohoto úkolu využijeme Steinerovu větu. Podle Steinerovy věty platí:
\[J_o = J_{o'} + md^2 \, ,\]
kde \(J_0\) je moment setrvačnosti vzhledem ke zkoumané ose \(o\), \(J_{o'}\) je moment setrvačnosti vzhledem k ose \(o'\) procházející těžištěm tělesa rovnoběžne s osou \(o\), \(m\) je hmotnost tělesa a d je vzdálenost \(\left| oo' \right|\).

K výpočtu budeme užívat soustavu souřadnic s počátkem v bodě \(A\).

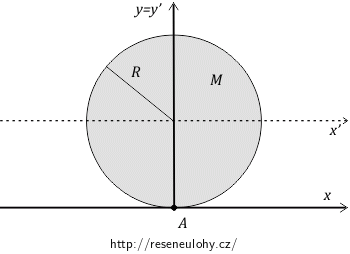
Čárkovaně jsou označeny souřadnice s počátkem v těžišti disku a nečárkovaně souřadnice s počátkem v bodě \(A\).

Osy \(y\) a \(y'\) splývají, vzdálenost os \(x\) a \(x'\) je stejná jako \(z\) a \(z'\).
\[\left| xx' \right| = \left| zz' \right| = R\]
Pomocí Steinerovy věty spočítáme momenty setrvačnosti vzhledem k novým souřadnicovým osám.
\[J_{xx} = J_{x'x'} + M R^2 = \frac{M R^2}{4} + M R^2 = \frac{5 M R^2}{4}\] \[J_{yy}=J_{y'y'} = \frac{M R^2}{4} .\] \[J_{zz} = J_{z'z'} + M R^2 = \frac{M R^2}{2} + M R^2 = \frac{3 M R^2}{2}\]
Posunutí ve směru osy \(y\) nám nepřináší žádnou nerovnováhu a proto budou deviační momenty stále nulové.

Matice tenzoru setrvačnosti tenkého disku vzhledem k bodu \(A\) bude tedy mít tvat:
\[J_M = \begin{pmatrix} \frac {5 M R^2}{4} & 0 & 0 \\ 0 & \frac {M R^2}{4} & 0 \\ 0 & 0 & \frac {3 M R^2}{2} \end{pmatrix} = \frac {M R^2}{4} \begin{pmatrix} 5 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 6 \end{pmatrix} \, .\]
Nápověda (C)1
Nakreslete si obrázek a určete souřadnice hmotného bodu (závaží).

Rozvažte, jakých vztahů budete užívat a jaké všechny veličiny k tomu budete potřebovat.
Řešení – Nápověda (C)1

Polohu hmotného bodu snadno určíme jako \(\left( R,\,R,\,0 \right)\).

Pro určení jednotlivých složek tenzoru setrvačnosti \(J_{jk}\) soustavy \(N\) hmotných bodů platí vztah:
\[J_{jk}= \sum_{i=1}^{N}{ m_{(i)}( \delta_{jk} \, r_{(i)}^2 - x_{(i)j} \, x_{(i)k} )}\]
kde \(i\) indexuje hmotné body o hmostnosti \(m_i\), \(r_i\) je vzdálenost \(i\)-tého bodu od počátku soustavy, \(\delta_{jk}\) je Kroneckerovo delta a souřadnice polohového vektoru \(x_{(i)l}\) pro \(l=\) 1 až 3 jsou obecnějším zapsáním našich souřadnic \(x, \, y, \, z\) pro \(i\)-tý bod.

Poznámka: Odvození tohoto vztahu viz například: Studijní text k teoretické mechanice tuhého tělesa.

V našem případě se vztah ještě zjednodušší, protože máme pouze 1 hmotný bod.
\[J_{jk}= m ( \delta_{jk} \, r^2 - x_j \, x_k )\]
Nápověda (C)2
Vypočítejte postupně jednotlivé složky tenzoru setrvačnosti hmotného bodu a zapište je do matice.
Řešení – Nápověda (C)2
Nejprve spočítejme složku \(J_{xx}\).
\[J_{xx} = J_{11} = m ( \delta_{11} \, r^2 - x_1 \, x_1 ) = m ( x^2 + y^2 + z^2 - x^2 ) = m (y^2 + z^2 ) = m R^2\]
Dále určíme složky \(J_{yy}\) a \(J_{zz}\).
\[J_{yy} = m (x^2 + z^2 ) = m R^2\] \[J_{zz} = m (x^2 + y^2 ) = m ( R^2 + R^2 ) = 2 m R^2\]
Pokračujme vypočítáním deviačních momentů.
\[J_{xy} = J_{12} = m ( \delta_{12} \, r^2 - x_1 \, x_2 ) = - m x y = - m R^2\] \[J_{xz} = - m x z = 0\] \[J_{yz} = - m y z = 0\]
Známe všechny potřebné složky a víme, že matice tenzoru setrvačnosti je symetrická, tak již zbývá ji jen zapsat.
\[J_m = m R^2 \begin{pmatrix} 1 & -1 & 0 \\ -1 & 1 & 0 \\ 0 & 0 & 2 \end{pmatrix} = \frac{M R^2}{4} \begin{pmatrix} 1 & -1 & 0 \\ -1 & 1 & 0 \\ 0 & 0 & 2 \end{pmatrix}\]
Řešení – Úloha (C)
Do obrázku si zakreslíme pouze soustavu souřadnic a polohu hmotného bodu.

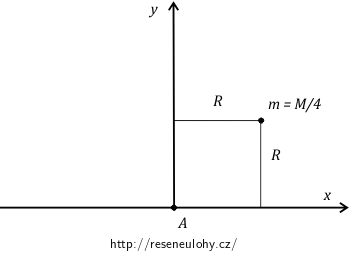
Poloha hmotného bodu je \(\vec r = \left( R \, , R \, , 0 \, \right)\).

K určení jednotlivých složek tenzoru setrvačnosti užijeme vztah
\[J_{jk}= m \left( \delta_{jk} \, r^2 - x_j \, x_k \right) \, .\]
Nejprve určíme složky odpovídající rotaci kolem souřadnicových os.
\[J_{xx} = J_{11} = m ( \delta_{11} \, r^2 - x_1 \, x_1 ) = m ( x^2 + y^2 + z^2 - x^2 ) = m (y^2 + z^2 ) = m R^2\] \[J_{yy} = m (x^2 + z^2 ) = m R^2\] \[J_{zz} = m (x^2 + y^2 ) = m ( R^2 + R^2 ) = 2 m R^2\]
Dále spočítáme deviační momenty.
\[J_{xy} = J_{12} = m ( \delta_{12} \, r^2 - x_1 \, x_2 ) = - m x y = - m R^2\] \[J_{xz} = - m x z = 0\] \[J_{yz} = - m y z = 0\]
Všechny složky zapíšeme do matice a máme hotovo.
\[J_m = m R^2 \begin{pmatrix} 1 & -1 & 0 \\ -1 & 1 & 0 \\ 0 & 0 & 2 \end{pmatrix} = \frac{M R^2}{4} \begin{pmatrix} 1 & -1 & 0 \\ -1 & 1 & 0 \\ 0 & 0 & 2 \end{pmatrix}\]
Nápověda (D)1
Rozmyslete si, jak se určí celkový tenzor setrvačnosti celého systému vzhledem k bodu A.
Řešení – Nápověda (D)1
Jelikož se tenzory setrvačnosti počítají pomocí sum či integrálů, pro každou složku celkového tenzoru \(J_c\) bude platit, že je součtem stejných složek tenzorů \(J_M\) a \(J_m\). Neboli tenzor celé soustavy je součtem tenzorů jednotlivých částí.
\[J_c = J_M + J_m = \frac {M R^2}{4} \begin{pmatrix} 5 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 6 \end{pmatrix} + \frac {M R^2}{4} \begin{pmatrix} 1 & -1 & 0 \\ -1 & 1 & 0 \\ 0 & 0 & 2 \end{pmatrix} = \frac {M R^2}{4} \begin{pmatrix} 6 & -1 & 0 \\ -1 & 2 & 0 \\ 0 & 0 & 8 \end{pmatrix}\]
Nápověda (D)2
Zavzpomínejte, jak se hledají vlastní vektory matice. Osvěžte si pojmy: vlastní čísla, vlastní vektor a charakteristický polynom.
Řešení – Nápověda (D)2
Nyní si zopakujme trochu lineární algebry.

Mějme čtvercovou matici \(A\) nad \(\mathbb{R}\). Pak vlastním vektorem \(\vec {v}\) matice \(A\) rozumíme nenulový vektor, pro nějž platí, že
\[A \vec v = \lambda \vec v ,\]
kde \(\lambda \in \mathbb{R}\). \(\lambda\) je vlastní číslo matice \(A\) příslušné vlastnímu vektoru \(\vec v\).
\[A \vec v - \lambda \vec v = \vec o\] \[\left( A - \lambda \mathbb{E} \right) \vec v = \vec o\]
Aby existovalo netriviální řešení této rovnice, musí být matice \(\left( A - \lambda \mathbb{E} \right)\) singulární, tedy musí platit:
\[\mathrm{det} \left| A - \lambda \mathbb{E} \right| = 0.\]
Tuto rovnici nazýváme charakterictickým polynomem a užíváme ji pro hledání vlastních čísel.

Jakmile nalezneme vlastní čísla, užijeme rovnice \(\left( A - \lambda \mathbb{E} \right) \vec v = \vec o\) k nalezení vlastních vektorů matice \(A\).
Nápověda (D)3
Najděte vlastní čísla a vektory matice
\[\begin{pmatrix} 6 & -1 & 0 \\ -1 & 2 & 0 \\ 0 & 0 & 8 \end{pmatrix} .\]
Řešení – Nápověda (D)3
Najděme kořeny charakteristického polynomu této matice.
\[\mathrm{det} \left| A - \lambda \mathbb{E} \right| = \begin{vmatrix} 6 - \lambda & -1 & 0 \\ -1 & 2 - \lambda & 0 \\ 0 & 0 & 8 - \lambda \end{vmatrix} = (8 - \lambda ) \left[ (6 - \lambda)(2 - \lambda ) -1 \right] = 0\]
Vidíme, že \(\lambda_1 = 8\) a dále stačí vyřešit kvadratickou rovnici v hranatých závorkách.
\[(6 - \lambda)(2 - \lambda ) - 1 = 0\] \[12 - 8 \lambda + \lambda^2 -1 = 0\] \[\lambda^2 - 8 \lambda + 11 = 0 \] \[\lambda_{2{,}3} = \frac {8 \pm \sqrt {64 - 44}}{2} = \frac {8 \pm \sqrt {20} }{2} = 4 \pm \sqrt 5\]
Tedy už známe všechna vlastní čísla.
\[\lambda_1 = 8 \, ; \, \lambda_2 = 4 + \sqrt 5 \, ; \, \lambda_3 = 4 - \sqrt 5\]
Najděme vlastní vektor \(\vec {v_1} = (x_1 , \, y_1 , \, z_1 )\) příslušný vlastnímu číslu \(\lambda_1\).
\[\left( A - \lambda_1 \mathbb{E} \right) \vec {v_1} = \begin{pmatrix} 6 - \lambda_1 & -1 & 0 \\ -1 & 2 - \lambda_1 & 0 \\ 0 & 0 & 8 - \lambda_1 \end{pmatrix} \vec {v_1} = \vec o\] \[\begin{pmatrix} -2 & -1 & 0 \\ -1 & -6 & 0 \\ 0 & 0 & 0 \end{pmatrix} \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} = \vec o\]
Máme soustavu rovnic:
\[\begin{matrix} 2 x_1 & + y_1 & = 0 ; \\ x_1 & + 6 y_1 & = 0 ; \end{matrix}\]
kterou splňuje pouze dvojice \([0, \, 0]\). Vidíme, že co se volby \(z\) týče, máme naprostou volnost. Pro jednoduchost zvolme \(z = 1\). Pak tedy platí pro vektor \(\vec {v_1}\) příslušný vlastnímu číslu \(\lambda_1 = 8\):
\[\vec {v_1}^T = (0 , \, 0 , \, 1 ) \, .\]
Dále hledejme vlastní vektor \(\vec {v_2} = (x_2 , \, y_2 , \, z_2 )\) příslušný vlastnímu číslu \(\lambda_2\).
\[\left( A - \lambda_2 \mathbb{E} \right) \vec {v_2} = \begin{pmatrix} 6 - \lambda_2 & -1 & 0 \\ -1 & 2 - \lambda_2 & 0 \\ 0 & 0 & 8 - \lambda_2 \end{pmatrix} \vec {v_2} = \vec o\] \[\begin{pmatrix} 2 - \sqrt 5 & -1 & 0 \\ -1 & -2 - \sqrt 5 & 0 \\ 0 & 0 & 4 - \sqrt 5 \end{pmatrix} \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} = \vec o\]
Dostáváme soustavu rovnic:
\[\begin{matrix} (2 - \sqrt 5 ) x_2 & - y_2 & = 0 ; \\ - x_2 & - (2 + \sqrt 5 ) y_2 & = 0 ; \end{matrix}\] \[( 4 - \sqrt 5 ) z_2 = 0 \, ,\]
ze které zjevně plyne, že \(z_2 = 0\). První dvě rovnice jsou lineárně závislé, z první vyjádříme \(y_2\).
\[ y_2 = (2 - \sqrt 5 ) x_2 \]
Opět vidíme, že máme volnost ve volbě parametru, pro jednoduchost vezměme \(x_2 = 1\). Pak tedy platí pro vektor \(\vec {v_2}\) příslušný vlastnímu číslu \(\lambda_2 = 4 + \sqrt 5\):
\[\vec {v_2}^T = (1 , \, 2 - \sqrt 5 , \, 0 ) \, .\]
Hledání vlastního vektoru \(\vec {v_3}\) příslušného vlastnímu číslu \(\lambda_3 = 4 - \sqrt 5\) si můžeme velmi zjednodušit. Podívejme se na postup hledání \(\vec {v_2}\) a jediné, co se v tomto postupu změní, je znaménko před \(\sqrt 5\). A proto bude pro vektor \(\vec {v_3}\) platit:
\[\vec {v_3}^T = (1 , \, 2 + \sqrt 5 , \, 0 ) \, .\]
Nápověda (D)4
Přiřaďte výsledkům nápovědy (D)3 fyzikální význam.

Rozmyslete, zda výsledky dávají fyzikálně smysl.
Řešení - Nápověda (D)4
Náš tenzor setrvačnosti celého systému měl tvar:
\[J_c = \frac {M R^2}{4} \begin{pmatrix} 6 & -1 & 0 \\ -1 & 2 & 0 \\ 0 & 0 & 8 \end{pmatrix} = \frac {M R^2}{4} A .\]
Určená vlastní čísla \(\lambda_i\) jsou vlastní čísla matice \(A\). Proto získáme hlavní momenty setrvačnosti \(J_i\) (tj. vlastní čísla matice \(J_c\)) prostým přepočtem \(J_i = \lambda_i \, \frac{M R^2}{4}\). Nalezené vlastní vektory \(\vec {v_i}\) odpovídají směrům hlavních os rotace s příslušnými hlavními momenty setrvačnosti \(J_i\).
\[\begin{matrix} J_1 = 8 \frac{M R^2}{4} = 2 M R^2 & & \vec {v_1} = (0 , \, 0 , \, 1 ) \\ J_2 = (4 + \sqrt 5)\frac{M R^2}{4} = (1 + \frac{\sqrt 5}{4} ) M R^2 & & \vec {v_2} = (1 , \, 2 - \sqrt 5 , \, 0 ) \\ J_3 = (4 - \sqrt 5)\frac{M R^2}{4} = (1 - \frac{\sqrt 5}{4} ) M R^2 & & \vec {v_3} = (1 , \, 2 + \sqrt 5 , \, 0 ) \end{matrix}\]
Vidíme, že první vlastní směr je shodný s osou \(z\). V tenzoru setrvačnosti celé soustavy \(J_c\) vidíme, že složka \(J_{zz}\) opravdu je \(2 M R^2\). Jelikož se jedná o ryze rovinný útvar, osu \(z\) bychom mezi hlavními osami měli čekat.

Dále si můžeme ověřit, že \(\vec {v_1}\) je kolmý na \(\vec {v_2}\) i \(\vec {v_3}\). Takovéto chování bychom u čistě rovinného útvaru čekali – jedna hlavní osa je kolmá na rovinu útvaru a zbylé dvě osy v této rovině leží. (Snad netřeba komentovat, že \(\vec {v_2}\) i \(\vec {v_3}\) v rovině \(xy\) opravdu leží.)
Poznámka k lineární algebře
Opět trochu zavzpomínejme na lineární algebru.

Máme-li matici \(A\), její vlastní čísla \(\lambda_i\) a vlastní vektory \(\vec v_i\), a když označíme \(P\) matici vytvořenou z vlastních vektorů \(\vec v_i\) zapsaných do sloupců, potom platí:
\[P^{-1} \cdot A \cdot P = \begin{pmatrix} \lambda_1 & 0 & 0 \\ 0 & \lambda_2 & 0 \\ 0 & 0 & \lambda_3 \end{pmatrix} .\]
Rozmysleme si, že \(P\) je matice přechodu od kanonické báze k bázi tvořené vlastními vektory.

Tedy bychom měli dostat diagonalizovanou matici. Ověřme to tedy pro náš případ tenzoru setrvačnosti.

Matice \(A\) je pro nás tenzorem setrvačnosti \(J_c\) celé soustavy.
\[J_c = \frac {M R^2}{4} \begin{pmatrix} 6 & -1 & 0 \\ -1 & 2 & 0 \\ 0 & 0 & 8 \end{pmatrix}\]
Vlastní čísla jsou pro nás hlavní momenty setrvačnosti \(J_i\) a k nim přísluší vlastní vektory \(\vec{v_i}\)
\[\begin{matrix} J_1 = 2 M R^2 & & \vec {v_1}^T = (0 , \, 0 , \, 1 ) \\ J_2 = (1 + \frac{\sqrt 5}{4} ) M R^2 & & \vec {v_2}^T = (1 , \, 2 - \sqrt 5 , \, 0 ) \\ J_3 = (1 - \frac{\sqrt 5}{4} ) M R^2 & & \vec {v_3}^T = (1 , \, 2 + \sqrt 5 , \, 0 ) \end{matrix}\]
V našem případě tedy matice \(P\) je ortogonální matice báze a má tvar:
\[P = \begin{pmatrix} 0 & 1 & 1 \\ 0 & 2 - \sqrt 5 & 2 + \sqrt 5 \\ 1 & 0 & 0 \end{pmatrix}\]
Najděme teď matici inverzního přechodu \(P^{-1}\).
\[\left(\begin{matrix} 0 & 1 & 1 \\ 0 & 2 - \sqrt 5 & 2 + \sqrt 5 \\ 1 & 0 & 0 \end{matrix}\right| \left.\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}\right) \sim \left(\begin{matrix} 1 & 0 & 0 \\ 0 & 2 - \sqrt 5 & 2 + \sqrt 5 \\ 0 & 1 & 1 \end{matrix}\right| \left.\begin{matrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{matrix}\right) \sim\] \[\sim \left(\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & \frac{2 + \sqrt 5}{2 - \sqrt 5} \\ 0 & 1 & 1 \end{matrix}\right| \left.\begin{matrix} 0 & 0 & 1 \\ 0 & \frac{1}{2 - \sqrt 5} & 0 \\ 1 & 0 & 0 \end{matrix}\right) \sim \left(\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & - \left(2 + \sqrt 5 \right)^2 \\ 0 & 0 & 1 + \left(2 + \sqrt 5 \right)^2 \end{matrix}\right| \left.\begin{matrix} 0 & 0 & 1 \\ 0 & - (2 + \sqrt 5) & 0 \\ 1 & 2 + \sqrt 5 & 0 \end{matrix}\right) \sim\] \[\sim \left(\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & - \left(9 + 4 \sqrt 5 \right) \\ 0 & 0 & 10 + 4 \sqrt 5 \end{matrix}\right| \left.\begin{matrix} 0 & 0 & 1 \\ 0 & - (2 + \sqrt 5) & 0 \\ 1 & 2 + \sqrt 5 & 0 \end{matrix}\right) \sim \left(\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 10 + 4 \sqrt 5 \end{matrix}\right| \left.\begin{matrix} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 1 & 2 + \sqrt 5 & 0 \end{matrix}\right) \sim\] \[\sim \left(\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{matrix}\right| \left.\begin{matrix} 0 & 0 & 1 \\ 1 & 0 & 0 \\ \frac{1}{10 + 4 \sqrt 5} & \frac{2 + \sqrt 5}{10 + 4 \sqrt 5} & 0 \end{matrix}\right) \sim \left(\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}\right| \left.\begin{matrix} 0 & 0 & 1 \\ \frac{9 + 4 \sqrt 5}{10 + 4 \sqrt 5} & - \frac{2 + \sqrt 5}{10 + 4 \sqrt 5} & 0 \\ \frac{1}{10 + 4 \sqrt 5} & \frac{2 + \sqrt 5}{10 + 4 \sqrt 5} & 0 \end{matrix}\right)\]
Vypočítejme tedy součin \(P^{-1} \cdot J_c \cdot P\).
\[P^{-1} \cdot J_c \cdot P = \begin{pmatrix} 0 & 0 & 1 \\ \frac{9 + 4 \sqrt 5}{10 + 4 \sqrt 5} & - \frac{2 + \sqrt 5}{10 + 4 \sqrt 5} & 0 \\ \frac{1}{10 + 4 \sqrt 5} & \frac{2 + \sqrt 5}{10 + 4 \sqrt 5} & 0 \end{pmatrix} \cdot \frac {M R^2}{4} \begin{pmatrix} 6 & -1 & 0 \\ -1 & 2 & 0 \\ 0 & 0 & 8 \end{pmatrix} \cdot \begin{pmatrix} 0 & 1 & 1 \\ 0 & 2 - \sqrt 5 & 2 + \sqrt 5 \\ 1 & 0 & 0 \end{pmatrix} =\] \[= \frac {M R^2}{4} \begin{pmatrix} 0 & 0 & 1 \\ \frac{9 + 4 \sqrt 5}{10 + 4 \sqrt 5} & - \frac{2 + \sqrt 5}{10 + 4 \sqrt 5} & 0 \\ \frac{1}{10 + 4 \sqrt 5} & \frac{2 + \sqrt 5}{10 + 4 \sqrt 5} & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & 4 + \sqrt 5 & 4 - \sqrt 5 \\ 0 & 3 - 2 \sqrt 5 & 3 + 2 \sqrt 5 \\ 8 & 0 & 0 \end{pmatrix} = \frac {M R^2}{4} \begin{pmatrix} 8 & 0 & 0 \\ 0 & 4 + \sqrt 5 & 0 \\ 0 & 0 & 4 - \sqrt 5 \end{pmatrix}\] \[P^{-1} \cdot J_c \cdot P = \begin{pmatrix} 2 M R^2 & 0 & 0 \\ 0 & (1 + \frac{\sqrt 5}{4} ) M R^2 & 0 \\ 0 & 0 & (1 - \frac{\sqrt 5}{4} ) M R^2 \end{pmatrix} = \begin{pmatrix} J_1 & 0 & 0 \\ 0 & J_2 & 0 \\ 0 & 0 & J_3 \end{pmatrix}\]
Vidíme tedy, že vzhledem k naší ortogonální bázi \(\vec{v_1}\), \(\vec{v_2}\) a \(\vec{v_3}\) má matice tenzoru setrvačnosti opravdu diagonální tvar, kde na hlavní diagonále jsou hlavní momenty setrvačnosti.
Řešení – Úloha (D)
Nejprve budeme potřebovat tenzor setrvačnosti celého systému \(J_c\). Ten určíme jako součet tenzorů setrvačnosti disku a závažíčka.
\[J_c = J_M + J_m = \frac {M R^2}{4} \begin{pmatrix} 5 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 6 \end{pmatrix} + \frac {M R^2}{4} \begin{pmatrix} 1 & -1 & 0 \\ -1 & 1 & 0 \\ 0 & 0 & 2 \end{pmatrix} = \frac {M R^2}{4} \begin{pmatrix} 6 & -1 & 0 \\ -1 & 2 & 0 \\ 0 & 0 & 8 \end{pmatrix} = \frac {M R^2}{4} A\]
Pro jednoduchost jsme matici v tenzoru setrvačnosti označili\(A\).

Nyní je třeba určit vlastní vektory a čísla matice tenzoru \(J_c\). Podrobný výpočet je proveden v sekci Řešení – Nápověda (D)3. Zde se odkažme na výpočetní techniku. Vlastní vektory i čísla matice se dají určit např. pomocí online dostupného Wolframu Alpha: výpočet vlastních vektorů a čísel matice tenzoru \(J_c\).

Následující tabulka ukazuje vlastní čísla \(\lambda_i\) a k nim přílsušné vlastní vektory \(\vec {v_i}\), které Wolfram Alpha určil.
\[\begin{matrix} \lambda_1 = 8 & & \vec {v_1} = (0 , \, 0 , \, 1 ) \\ \lambda_2 = 4 + \sqrt 5 & & \vec {v_2} = (- 2 - \sqrt 5 , \, 1 , \, 0 ) \\ \lambda_3 = 4 - \sqrt 5 & & \vec {v_3} = (-2 + \sqrt 5 , \, 1 , \, 0 ) \end{matrix}\]
Po jednoduché úpravě (přenásobení \(\vec {v_2}\) výrazem \(2 - \sqrt 5\) a \(\vec {v_3}\) výrazem \(2 + \sqrt 5\)) dostáváme i vizuálně stejný výsledek jako při ručním výpočtu.
\[\begin{matrix} \vec {v_1} = (0 , \, 0 , \, 1 ) \\ \vec {v_2} = (1 , \, 2 - \sqrt 5 , \, 0 ) \\ \vec {v_3} = (1 , \, 2 + \sqrt 5 , \, 0 ) \end{matrix}\]
Náš tenzor setrvačnosti celého systému měl tvar:
\[J_c = \frac {M R^2}{4} \begin{pmatrix} 6 & -1 & 0 \\ -1 & 2 & 0 \\ 0 & 0 & 8 \end{pmatrix} = \frac {M R^2}{4} A .\]
Určená vlastní čísla \(\lambda_i\) jsou vlastní čísla matice \(A\). Proto získáme hlavní momenty setrvačnosti \(J_i\) (tj. vlastní čísla matice \(J_c\)) prostým přepočtem \(J_i = \lambda_i \, \frac{M R^2}{4}\). Nalezené vlastní vektory \(\vec {v_i}\) odpovídají směrům hlavních os rotace s příslušnými hlavními momenty setrvačnosti \(J_i\).
\[\begin{matrix} J_1 = 2 M R^2 & & \vec {v_1} = (0 , \, 0 , \, 1 ) \\ J_2 = (1 + \frac{\sqrt 5}{4} ) M R^2 & & \vec {v_2} = (1 , \, 2 - \sqrt 5 , \, 0 ) \\ J_3 = (1 - \frac{\sqrt 5}{4} ) M R^2 & & \vec {v_3} = (1 , \, 2 + \sqrt 5 , \, 0 ) \end{matrix}\]
Vidíme, že první vlastní směr je shodný s osou \(z\). V tenzoru setrvačnosti celé soustavy \(J_c\) vidíme, že složka \(J_{zz}\) opravdu je \(2 M R^2\). Jelikož se jedná o ryze rovinný útvar, osu \(z\) bychom mezi hlavními osami měli čekat.

Dále je vidět, že \(\vec {v_1}\) je kolmý na \(\vec {v_2}\) i \(\vec {v_3}\). Takovéto chování bychom u čistě rovinného útvaru čekali – jedna hlavní osa je kolmá na rovinu útvaru a zbylé dvě osy v této rovině leží. (Snad netřeba komentovat, že \(\vec {v_2}\) i \(\vec {v_3}\) v rovině \(xy\) opravdu leží.)

Pokud se snažíte si celou situaci představit, mohl by následující 3D model v programu GeoGebra poskytnout Vaší představivosti malou berličku.
Odpověď
(A) Tenzor setrvačnosti \(J_S\) tenkého homogenního disku vzhledem k jeho hmotnému středu má tvar:
\[J_S = \frac {M R^2}{4} \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{pmatrix} . \]
(B) Matice tenzoru setrvačnosti \(J_M\) tenkého homogenního disku vzhledem k bodu A má tvar:
\[J_M = \frac {M R^2}{4} \begin{pmatrix} 5 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 6 \end{pmatrix} . \]
(C) Tenzor setrvačnosti \(J_m\) samotného hmotného bodu vzhledem k bodu \(A\) má tvar:
\[J_m = \frac {M R^2}{4} \begin{pmatrix} 1 & -1 & 0 \\ -1 & 1 & 0 \\ 0 & 0 & 2 \end{pmatrix} .\]
(D) Tenzor setrvačnosti \(J_c\) celého systému je:
\[J_c = \frac {M R^2}{4} \begin{pmatrix} 6 & -1 & 0 \\ -1 & 2 & 0 \\ 0 & 0 & 8 \end{pmatrix}\]
Vektory \(\vec {v_i}\) určují hlavní osy rotace s příslušnými hlavními momenty setrvačnosti \(J_i\).
\[\begin{matrix} J_1 = 2 M R^2 & & \vec {v_1}^T = (0 , \, 0 , \, 1 ) \\ J_2 = (1 + \frac{\sqrt 5}{4} ) M R^2 & & \vec {v_2}^T = (1 , \, 2 - \sqrt 5 , \, 0 ) \\ J_2 = (1 - \frac{\sqrt 5}{4} ) M R^2 & & \vec {v_3}^T = (1 , \, 2 + \sqrt 5 , \, 0 ) \end{matrix}\]