Dva vozíky s pružinkou
Úloha číslo: 635
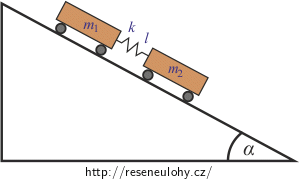
Dva vozíčky hmotnosti m1, m2 spojené pružinkou délky l a tuhosti k sjíždějí po nakloněné rovině se sklonem α.
A) Napište lagrangián soustavy, přičemž za zobecněné zvolte souřadnice hmotných středů obou vozíčků (ve směru podél nakloněné roviny) a označte je x1, x2.
B) Napište lagrangián v zobecněných souřadnicích hmotného středu soustavy dvou vozíčků X a jejich relativní vzdálenosti ξ.
Sestavte a vyřešte Lagrangeovy rovnice II. druhu.
| |
| A) L(x1, x2) | 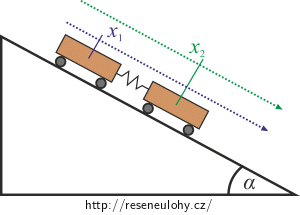
|
| B) L(X, ξ) | 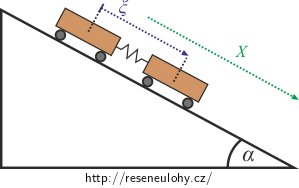
|
Nápověda – potenciální energie pružiny
Pružina tuhosti k a klidové délky l je v rovnovážné poloze, zaujímá-li právě délku l. Silové působení vyvolává její stlačení nebo uvolnění, tedy posun z rovnovážné polohy. Pro sílu pružnosti a potenciální energii pružiny obecné délky y tady můžeme psát:
\[F_y = -k(y-l)\] \[V(y) = \frac{1}{2}k(y-l)^2.\]Vyjádřete potenciální energii postupně pomocí obou souřadnic ze zadání.
Nápověda – kinetická energie v L(X, ξ)
Je snadné určit, že kinetická energie vyjádřená pomocí souřadnic x1, x2 bude:
\[T (x_1, x_2) = \frac{1}{2}m_1\dot{x}^2_1 + \frac{1}{2}m_2\dot{x}^2_2.\]Kinetickou energii v souřadnicích X, ξ určíme s pomocí znalosti kinetické energie jako funkce x1, x2.
Napište transformační vztahy mezi těmito souřadnicemi. Spočtěte první derivaci podle času a dosaďte do vyjádření T(x1, x2).
Řešení – lagrangián L(x1, x2)
Potenciální energii VG, kterou vozíčky mají vzhledem ke své poloze v tíhovém poli, určíme stejně, jako v úloze Hmotný bod na nakloněné rovině:
\[V_G(x_1, x_2) = -m_1gx_1\sin\alpha - m_2gx_2\sin\alpha\ .\]Kinetickou energii a potenciální energii pružnosti jsme určovali výše. Po dosazení všech členů dostáváme:
\[L(x_1, x_2) = \frac{1}{2}m_1\dot{x_1}^2 + \frac{1}{2}m_2\dot{x_2}^2 + (x_1m_1+x_2m_2)g\sin\alpha - \frac{1}{2}k(x_2-x_1-l)^2\ .\]Řešení – lagrangián L(X, ξ)
Kinetickou energii vozíčků a potenciální energii pružiny v těchto souřadnicích jsme určovali v předchozích sekcích. Zbývá vyjádřit potenciální energii soustavy dvou vozíčků v tíhovém poli VG, což bude:
\[V_{G}(X) = -MgX\sin \alpha\ .\]Odtud lagrangián:
\[L = \frac{1}{2}M\dot{X}^2 + \frac{1}{2}\mu\dot{\xi}^2 + MgX\sin \alpha - \frac{1}{2}k(\xi-l)^2\ ,\]kde pro M a μ platí:
\[M = m_1+m_2\ ,\] \[\mu = \frac{m_1m_2}{m_1+m_2}\ .\]Řešení – Lagrangeovy rovnice II. druhu pro L(x1, x2)
Nejdříve sestavíme Lagrangeovy rovnice. Nachystáme si příslušné derivace lagrangiánu:
\[\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial}{\partial\dot{x_1}}L(x_1, x_2) = m_1\ddot{x}_1\] \[\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial}{\partial\dot{x_2}}L(x_1, x_2) = m_2\ddot{x}_2\] \[\frac{\partial}{\partial x_1}L(x_1, x_2) = m_1g\sin\alpha -k(x_2 - x_1 - l)\] \[\frac{\partial}{\partial x_2}L(x_1, x_2) = m_2g\sin\alpha +k(x_2 - x_1 - l)\]a dostáváme soustavu:
\[m_1\ddot{x_1} - m_1g\sin\alpha + k(x_2 - x_1 - l) = 0\] \[m_2\ddot{x_2} - m_2g\sin\alpha - k(x_2 - x_1 - l) = 0.\]Řešení – Lagrangeovy rovnice II. druhu pro L(X, ξ)
I zde si nejprve si nachystáme potřebné derivace lagrangiánu:
\[\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial}{\partial\dot{X}}L(X, \xi) = M\ddot{X}\] \[\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial}{\partial\dot{\xi}}L(X, \xi) = \mu\ddot{\xi}\] \[\frac{\partial}{\partial X}L(X, \xi) = Mg\sin\alpha\] \[\frac{\partial}{\partial\xi}L(X, \xi) = -k(\xi - l)\]a potom sestavíme Lagrangeovy rovnice:
\[\ddot{X} - g\sin\alpha = 0\] \[\mu\ddot{\xi} + k(\xi - l) = 0.\]Řešení rovnic
Řešme nejdříve rovnici popisující pohyb hmotného středu soustavy:
\[\ddot{X} - g\sin\alpha = 0\ .\]Ta je zcela analogická rovnici z úlohy Hmotný bod na nakloněné rovině a jejím řešením po dvojím zintegrování a určení fyzikálního významu konstant je:
\[X(t) = \frac{1}{2}gt^2\sin \alpha + v_{0}t + X_0\ ,\]kde v0 je počáteční rychlost hmotného středu a X0 počáteční souřadnice hmotného středu. Celá soustava se tedy pohybuje dolů po nakloněné rovině rovnoměrně zrychleně.
V druhém vztahu můžeme vidět rovnici lineárního harmonického oscilátoru (viz např. úloha Jednorozměrný harmonický oscilátor).
\[\mu\ddot{\xi} + k(\xi - l) = 0\ .\]Jedinou drobnou odchylku od zaužívaného tvaru odstraníme zavedením pomocné souřadnice:
\[\tilde{\xi} = \xi - l\] \[\ddot{\tilde{\xi}} = \ddot{\xi}.\]Dostáváme rovnici:
\[\mu\ddot{\tilde{\xi}} + k\tilde{\xi} = 0\ .\]Tato rovnice má řešení:
\[\tilde{\xi}(t) = A\sin\left(\sqrt{\frac{k}{\mu}}t+\varphi_0\right)\ ,\]respektive:
\[\xi(t) = A\sin\left(\sqrt{\frac{k}{\mu}}t+\varphi_0\right) + l\ .\]Nyní můžeme řešení obou rovnic použít k získání řešení v souřadnicích x1, x2.
Odpověď
Lagrangiány v obou soustavách souřadnic jsou:
\[L(x_1, x_2) = \frac{1}{2}m_1\dot{x_1}^2 + \frac{1}{2}m_2\dot{x_2}^2 + (x_1m_1+x_2m_2)g\sin\alpha - \frac{1}{2}k(x_2-x_1-l)^2\] \[L(X, \xi) = \frac{1}{2}M\dot{X}^2 + \frac{1}{2}\mu\dot{\xi}^2 + MgX\sin \alpha - \frac{1}{2}k(\xi-l)^2.\]Těm odpovídají soustavy rovnic:
\[m_1\ddot{x_1} - m_1g\sin\alpha + k(x_2 - x_1 - l) = 0\] \[m_2\ddot{x_2} - m_2g\sin\alpha - k(x_2 - x_1 - l) = 0\]a
\[\ddot{X} - g\sin\alpha = 0\] \[\mu\ddot{\xi} + k(\xi - l) = 0\ .\]Jejich řešeními jsou funkce:
\[X(t) = \frac{1}{2}gt^2\sin \alpha + v_{0}t + X_0\] \[\xi(t) = A\sin (\omega t +\varphi_0) +l\]a
\[x_1 (t) = \frac{1}{2}gt^2\sin \alpha + v_{0}t + X_0 - \frac{m_2}{m_1+m_2}[A\sin (\omega t +\varphi_0) +l]\] \[x_2 (t) = \frac{1}{2}gt^2\sin \alpha + v_{0}t + X_0 + \frac{m_1}{m_1+m_2}[A\sin (\omega t +\varphi_0) +l]\ ,\]kde v0, X0, A a φ0 jsou konstanty dány počátečními podmínkami a pro úhlovou frekvenci kmitů platí:
\[\omega = \sqrt{\frac{k}{\mu}}\ ,\]kde
\[\mu = \frac{m_1m_2}{m_1+m_2}\ .\]


