Tenzor setrvačnosti válce
Úloha číslo: 2251
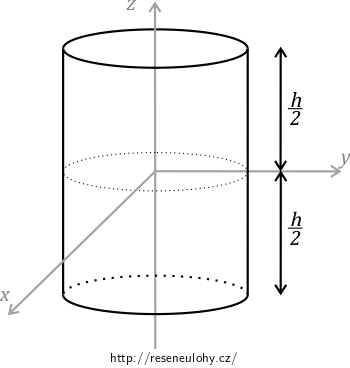
Mějme homogenní válec výšky \(h\) a kruhové podstavy o poloměru \(R\).
Nápověda (A)1
Rozvažte, jakých vztahů budete užívat a jaké všechny veličiny budete potřebovat při výpočtu tenzoru setrvačnosti.
Dále si rozmyslete, v jakých souřadnicích bude výhodné pracovat, jaké platí transformační vztahy a jaký je význam determinantu Jacobiho matice (jakobiánu). Určete jakobián.
Nápověda (A)2
Vypočítejte postupně jednotlivé složky tenzoru setrvačnosti a zapište je do matice.
Řešení – (A)
Pro určení složek tenzoru setrvačnosti \(J_{jk}\) spojitého tělesa platí vztah:
\[J_{jk}= \int_V^{}{( \delta_{jk} \, r^2 - x_j \, x_k ) \rho} \, \mathrm{d}V,\tag{1}\]kde \(r\) je vzdálenost od počátku soustavy, \(\delta_{jk}\) je Kroneckerovo delta, \(\rho\) je hustota tělesa a souřadnice polohového vektoru \(x_i\) pro \(i=\) 1 až 3 jsou obecnějším zapsáním našich souřadnic \(x, \, y, \, z\).
Tenzor setrvačnosti válce bude lepší počítat v cylindrických souřadnicích
\[x = r \cos \varphi \, ,\] \[y = r \sin \varphi \, ,\] \[z = z \, ,\]kde \(r\) je vzdálenost od osy \(z\), probíhající interval \( \left( 0,R \right\rangle \). Úhel \(\varphi\) je měřený od osy \(x\) v rovině \(xy\) proti směru hodinových ručiček a \(\varphi \in \left( 0, 2 \pi \right\rangle \). Jelikož počátek naší soustavy souřadnic splývá s těžištěm válce, je \(z \in \left\langle -\frac{h}{2};\, \frac{h}{2} \right\rangle\).
Při počítání objemových integrálů v cylindrických souřadnicích je třeba uvažovat jakobián \(\left| \mathbb{J} \right|\).
\[\int_V f(x,y,z) \,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z = \int_V f(r,\varphi,z) \left| \mathbb{J} \right|\,\mathrm{d}r\,\mathrm{d}\varphi\,\mathrm{d}z\]Nyní určíme jakobián pro cylindrické souřadnice.
\[\left| \mathbb{J} \right| = \begin{vmatrix} \frac{\mathrm{d}x}{\mathrm{d}r} & \frac{\mathrm{d}x}{\mathrm{d}\varphi} & \frac{\mathrm{d}x}{\mathrm{d}z}\\ \frac{\mathrm{d}y}{\mathrm{d}r} & \frac{\mathrm{d}y}{\mathrm{d}\varphi} & \frac{\mathrm{d}y}{\mathrm{d}z}\\ \frac{\mathrm{d}z}{\mathrm{d}r} & \frac{\mathrm{d}z}{\mathrm{d}\varphi} & \frac{\mathrm{d}z}{\mathrm{d}z} \end{vmatrix} = \begin{vmatrix} \cos \varphi & - r \,\sin \varphi & 0 \\ \sin \varphi & r \, \cos \varphi & 0 \\ 0 & 0 & 1 \end{vmatrix} = + 1 \begin{vmatrix} \cos\varphi & - r \,\sin\varphi \\ \sin\varphi & r \,\cos\varphi \end{vmatrix} = r \cos^2\varphi + r \sin^2\varphi = r \]Složky \(J_{xx}\) a \(J_{yy}\) musí být stejné, protože rozložení „hmoty“ válce vzhledem k osám \(x\) a \(y\) je zcela totožné.
Určeme složku \(J_{xx}\):
\[J_{xx}=J_{11}= \int_V {\left ( \delta_{11} \, r^2 - x_1 x_1 \right) \,\rho} \,\mathrm{d}x \,\mathrm{d}y \,\mathrm{d}z = \int_V {\left ( x^2 + y^2 + z^2 - x^2 \right ) \,\rho} \,\mathrm{d}x \,\mathrm{d}y \,\mathrm{d}z =\int_V {\left ( y^2 + z^2 \right ) \,\rho} \,\mathrm{d}x \,\mathrm{d}y \,\mathrm{d}z .\]Nyní přejdeme do cylindrických souřadnic a dosadíme za \(y\) a \(z\).
\[J_{xx} = \int_0^{2\pi} \int_0^R \int_{-\frac{h}{2}}^{\frac{h}{2}} {\left( r^2 \sin^2\varphi + z^2 \right)\, r \, \rho} \,\mathrm{d}z \,\mathrm{d}r \,\mathrm{d}\varphi = \rho \int_0^{2\pi} \int_0^R {\left[ z\, r^2 \sin^2\varphi + \frac{z^3}{3} \right]_{-\frac{h}{2}}^{\frac{h}{2}}} \,r\,\mathrm{d}r \,\mathrm{d}\varphi = \] \[= \rho \int_0^{2\pi} \int_0^R {\left( h \, r^2 \sin^2\varphi + \frac{h^3}{12} \right)} \,r\,\mathrm{d}r \,\mathrm{d}\varphi = h\,\rho \int_0^{2\pi} \int_0^R {\left( r^3 \sin^2\varphi + r\,\frac{h^2}{12} \right)} \,\mathrm{d}r \,\mathrm{d}\varphi =\] \[= h\,\rho \int_0^{2\pi} {\left[ \frac{r^4}{4} \sin^2\varphi + \frac{r^2}{2}\,\frac{h^2}{12} \right]_0^R} \,\mathrm{d}\varphi = h\,\rho \int_0^{2\pi} {\left( \frac{R^4}{4} \sin^2\varphi + \frac{R^2}{4}\,\frac{h^2}{6} \right)} \,\mathrm{d}\varphi =\] \[= h\,\rho\,\frac{R^2}{4} \int_0^{2\pi} {\left( R^2 \sin^2\varphi + \frac{h^2}{6} \right)} \,\mathrm{d}\varphi = \frac{h\,\rho\,R^2}{4} \left( \int_0^{2\pi} {R^2 \sin^2\varphi} \,\mathrm{d}\varphi + \int_0^{2\pi} {\frac{h^2}{6}} \,\mathrm{d}\varphi \right)\] \[\int_0^{2 \pi} \sin^2 \varphi \,\mathrm{d}\varphi = \int_0^{2 \pi} \frac {1 - \cos 2 \varphi}{2} \,\mathrm{d}\varphi = \left [ \frac {\varphi}{2} - \frac {\sin 2 \varphi}{4} \right ]_0^{2 \pi}= \pi\] \[J_{xx} = \frac{h\,\rho\,R^2}{4} \left(\pi\, R^2 + \pi\, \frac{h^2}{3} \right) = \frac{\rho\,h\,\pi\,R^2}{4} \left(R^2 + \frac{h^2}{3} \right) \]Vztah \(\rho\,h\,\pi\,R^2\) odpovídá hmotnosti válce \(M\). Pak pro složky \(J_{xx}\) a \(J_{yy}\) máme vztah:
\[J_{yy} = J_{xx}=\frac{M}{4} \left(R^2 + \frac{h^2}{3} \right) .\]Další na řadě je složka \(J_{zz}\).
\[J_{zz}=J_{33}= \int_V {\left ( \delta_{33} \, r^2 - x_3 x_3\right) \,\rho} \,\mathrm{d}x \,\mathrm{d}y \,\mathrm{d}z = \int_V {\left ( x^2 + y^2 + z^2 - z^2 \right ) \,\rho} \,\mathrm{d}x \,\mathrm{d}y \,\mathrm{d}z =\int_V {\left ( x^2 + y^2 \right ) \,\rho} \,\mathrm{d}x \,\mathrm{d}y \,\mathrm{d}z = \] \[= \int_0^{2\pi} \int_0^R \int_{-\frac{h}{2}}^{\frac{h}{2}} {\left( r^2 \cos^2\varphi + r^2 \sin^2\varphi \right)\, r \, \rho} \,\mathrm{d}z \,\mathrm{d}r \,\mathrm{d}\varphi = \rho \int_0^{2\pi} \int_0^R \int_{-\frac{h}{2}}^{\frac{h}{2}} {\left( \cos^2\varphi + \sin^2\varphi \right)\, r^3 } \,\mathrm{d}z \,\mathrm{d}r \,\mathrm{d}\varphi =\] \[= \rho \int_0^{2\pi} 1 \,\mathrm{d}\varphi \int_{-\frac{h}{2}}^{\frac{h}{2}} 1 \,\mathrm{d}z \int_0^R r^3 \,\mathrm{d}r = \rho 2 \pi h \left[ \frac{r^4}{4} \right]_0^R = \frac{1}{2} \rho\pi h R^4 = \frac{1}{2} M R^2\]Tedy jsme pro složku tenzoru setrvačnosti \(J_{zz}\) odvodili vztah:
\[J_{zz} = \frac{1}{2} M R^2 .\]Teď se podívejme na deviační momenty.
Rozložení „hmoty“ okolo os soustavy je velmi symetrické, a proto budou deviační momenty nulové.
(Ověření viz Tenzor setrvačnosti válce, Řešení – Nápověda (A)2)
Nakonec zapíšeme všechny složky do matice.
\[J_{válec} = \begin{pmatrix} \frac{M}{4} \left(R^2 + \frac{h^2}{3} \right) & 0 & 0 \\ 0 & \frac{M}{4} \left(R^2 + \frac{h^2}{3} \right) & 0 \\ 0 & 0 & \frac{M}{2} R^2 \end{pmatrix} = \frac {M}{4} \begin{pmatrix} \left(R^2 + \frac{h^2}{3} \right) & 0 & 0 \\ 0 & \left(R^2 + \frac{h^2}{3} \right) & 0 \\ 0 & 0 & 2 R^2 \end{pmatrix} \]Řešení – (B)
Po určení tenzoru \(J\) už je úloha (B) dosti snadná.
Přímo spočítáme zadané limity a začněme \(\lim_{h \to 0} J_{válec}\). Válec s infinitezimální výškou je rovinný disk. Označme proto \(J_{disk}=\lim_{h \to 0} J_{válec}\), potom by pro tenzor setrvačnosti disku mělo platit následující.
\[J_{disk}=\lim_{h \to 0} J_{válec} = \lim_{h \to 0} \frac {M}{4} \begin{pmatrix} \left(R^2 + \frac{h^2}{3} \right) & 0 & 0 \\ 0 & \left(R^2 + \frac{h^2}{3} \right) & 0 \\ 0 & 0 & 2 R^2 \end{pmatrix} = \frac {M}{4} \begin{pmatrix} R^2 & 0 & 0 \\ 0 & R^2 & 0 \\ 0 & 0 & 2 R^2 \end{pmatrix}\] \[J_{disk}=\frac {M R^2}{4} \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{pmatrix}\]Tento výsledek opravdu odpovídá výsledku úlohy Tenzor setrvačnosti tenkého disku.
Nyní se podívejme na \(\lim_{R \to 0} J_{válec}\). Válec s infinitezimálním poloměrem podstavy odpovídá velmi tenké tyči. Označme proto \(J_{tyč}=\lim_{R \to 0} J_{válec}\), potom tenzor setrvačnosti tenké tyče můžeme odvodit podobným postupem.
\[J_{tyč}=\lim_{R \to 0} J_{válec} = \lim_{R \to 0} \frac {M}{4} \begin{pmatrix} \left(R^2 + \frac{h^2}{3} \right) & 0 & 0 \\ 0 & \left(R^2 + \frac{h^2}{3} \right) & 0 \\ 0 & 0 & 2 R^2 \end{pmatrix} =\frac {M}{4} \begin{pmatrix} \frac{h^2}{3} & 0 & 0 \\ 0 & \frac{h^2}{3} & 0 \\ 0 & 0 & 0 \end{pmatrix} \] \[J_{tyč}=\frac {M h^2}{12} \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{pmatrix}\]Tento výsledek odpovídá tenzoru setrvačnosti velmi tenké tyče délky \(h\), viz úloha Tenzor setrvačnosti tyče.
Odpověď
Tenzor setrvačnosti homogenního válce výšky \(h\) a kruhové podstavy o poloměru \(R\) vzhledem k jeho těžišti má tvar:
\[J_{válec} = \frac {M}{4} \begin{pmatrix} \left(R^2 + \frac{h^2}{3} \right) & 0 & 0 \\ 0 & \left(R^2 + \frac{h^2}{3} \right) & 0 \\ 0 & 0 & 2 R^2 \end{pmatrix} .\]\(\lim_{h \to 0} J_{válec}\) má význam tenzoru setrvačnosti \(J_{disk}\) tenkého disku vzhledem k jeho středu.
\[J_{disk}=\frac {M R^2}{4} \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{pmatrix} \]\(\lim_{R \to 0} J_{válec}\) má význam tenzoru setrvačnosti \(J_{tyč}\) tenké tyče délky \(h\) vzhledem k jejímu středu.
\[J_{tyč}=\frac {M h^2}{12} \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{pmatrix}\]