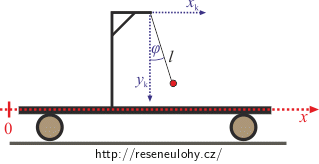
Vozík s kyvadlem

Úloha číslo: 634

Napište lagrangián vozíčku hmotnosti M pohybujícího se po vodorovné podložce. Na vozíčku je umístěno matematické kyvadlo (hmotný bod na nehmotném závěsu) hmotnosti m a délky l.

Sestavte a vyřešte Lagrangeovy rovnice II. druhu.

Nápověda – volba souřadnic
Ujasněte si, kolik má systém stupňů volnosti, a kolik tedy budeme potřebovat zobecněných souřadnic.

Nezapomínejte, že se nemusíte pokoušet zvolit jeden z běžně používaných typů soustav souřadnic (kartézské, polární...), ale vyberte takové zobecněné souřadnice, které skutečně nejvýhodněji popisují pohyb vozíku a kyvadla.
Volba souřadnic
Vozíček pohybující se jedním směrem po vodorovné podložce má jeden stupeň volnosti. Další stupeň volnosti má matematické kyvadlo. Celkem budeme tedy potřebovat dvě zobecněné souřadnice.

Kartézské souřadnice pomocí kterých dobře popíšeme pohyb kyvadla budeme značit s indexem k (viz obrázek). Budeme je však považovat za pevné, tj. ne spojené s úchytem kyvadla, který se pophybuje spolu s vozíkem.

Nejjednodušší bude zvolit jako zobecněné souřadnice x-ovou souřadnici pohybu vozíčku a úhel φ pro výchylku kyvadla.
Nápověda – kinetická energie
Určit kinetickou energii vozíku nebude problém. Jak se ale rychlost vozíku projeví na kinetické energii kyvadla?
Řešení nápovědy
Rychlost vozíku je součástí vodorovné složky rychlosti závaží matematického kyvadla (z hlediska podložky, po které se pohybuje vozík). Rozdělíme tedy vektor rychlosti závaží na vodorovný a kolmý směr a rychlost vozíku přičteme pouze k vodorovné složce.
Řešení – kinetická energie
Kinetickou energii vozíku T_v určíme snadno:
\[T_v = \frac{1}{2}M\dot{x}^2\ .\]
O něco složitější to bude s kinetickou energií kyvadla. V souřadnicích x_k, y_k vyjádříme polohu kyvadla. Nezapomeňte na posun souřadnice x_k kvůli poloze vozíčku.
\[x_k = l\sin \varphi + x\] \[y_k = l\cos \varphi\]
Derivováním podle času dostaneme:
\[v_{kx} = l\dot{\varphi} \cos \varphi + \dot{x}\] \[v_{ky} = -l\dot{\varphi} \sin \varphi\]
Pro druhou mocninu velikosti rychlosti kyvadla v_k tedy dostáváme:
\[|\vec{v_k}|^2 = v_{kx}^2 + v_{ky}^2 = l^2\dot{\varphi}^2 + \dot{x}^2 + 2l\dot{\varphi}\dot{x}\cos \varphi\ .\]
Odtud tedy pro kinetickou energii kyvadla na vozíčku T_k platí:
\[T_k = \frac{1}{2}ml^2\dot{\varphi}^2 + \frac{1}{2}m\dot{x}^2 + ml\dot{\varphi}\dot{x}\cos \varphi\ .\]
Pro celkovou kinetickou energii systému platí:
\[T = T_k + T_v = \frac{1}{2}(M+m)\dot{x}^2 + \frac{1}{2}ml^2\dot{\varphi}^2 + ml\dot{\varphi}\dot{x}\cos \varphi\ .\]
Komentář – součet kinetických energií
Pro skládání rychlostí platí princip superpozice. Nesmíme se však nechat zlákat přitažlivou představou, že podobně jednoduše lze skládat i kinetické energie spočtené z jednotlivých rychlostí.

Není tomu tak! Nelineární chování způsobuje to, že kinetická energie závisí na rychlosti kvadraticky. Kdybychom spočetli kinetickou energii pouze jako součet energie kývání kyvadla a nezávisle na ní energie pohybu vozíčku, chyběl by nám důležitý křížový člen \(ml\dot{\varphi}\dot{x}\cos \varphi\), kvůli kterému nebudou Lagrangeovy rovnice II. druhu nezávislé, ale budou tvořit soustavu. Tedy fyzikálně řečeno, pohyby kyvadla a vozíku nebudou probíhat nezávisle.
Řešení – potenciální energie
Budeme postupovat stejně jako v úloze Matematické kyvadlo. Nulovou hladinu potenciální energie zvolíme v místě uchycení kyvadla na vozíčku. Vozíček jako takový má potenciální energii konstantní a pro kyvadlo platí:
\[V = -mgl\cos\varphi\ .\]
Řešení – lagrangián
Obecný předpis Lagrangeovy funkce je:
\[L = T-V\ .\]
Po dosazení vyjádření obou energií z předchozích oddílů dostáváme lagrangián této soustavy:
\[L = \frac{1}{2}(M+m)\dot{x}^2 + \frac{1}{2}ml^2\dot{\varphi}^2 + ml\dot{\varphi}\dot{x}\cos\varphi + mgl\cos\varphi\ .\]
Nápověda – aproximace
Použijte přibližné vzorce, resp. Taylorův rozvoj, a upravte lagrangián pro případ malých kmitů kyvadla a malých rychlostí kývání. Zanedbejte členy třetího a vyššího řádu malosti.
Vzorce
Potřebujeme de facto pouze jediný vzorec, a sice:
\[\cos \varphi \approx 1 - \frac{1}{2}\varphi^2\]
pro φ malá.

Pozor na vzájemné násobení členů, které považujeme za malé! Zejména při násobení malých výchylek s malými rychlostmi. Můžeme tak dostat zanedbatelný člen.
Řešení – aproximace
Vyjádřili jsme lagrangián ve tvaru:
\[L = \frac{1}{2}(M+m)\dot{x}^2 + \frac{1}{2}ml^2\dot{\varphi}^2 + ml\dot{\varphi}\dot{x}\cos\varphi + mgl\cos\varphi\ .\]
Rozebereme ho teď člen po členu. V prvních dvou není nic k aproximaci.

Pro třetí člen dostáváme:
\[ml\dot{\varphi}\dot{x}\cos \varphi \approx ml\dot{\varphi}\dot{x}\left(1-\frac{1}{2}\varphi^2\right) = ml\dot{\varphi}\dot{x} - \frac{1}{2}ml\dot{\varphi}\dot{x}\varphi^2\ .\]
Poslední člen z výrazu po aproximaci je ovšem malý čtvrtého řádu. Použijeme tedy přiblížení:
\[ml\dot{\varphi}\dot{x}\cos \varphi \approx ml\dot{\varphi}\dot{x}\ .\]
Aproximaci posledního členu lagrangiánu už známe z úlohy Matematické kyvadlo:
\[mgl\cos \varphi \approx mgl\left(1-\frac{1}{2}\varphi^2\right) = -\frac{1}{2}mgl\varphi^2 + konst.\]
Po zanedbání konstanty tedy dostáváme lagrangián:
\[\tilde{L} = \frac{1}{2}(M+m)\dot{x}^2+\frac{1}{2}ml^2\dot{\varphi}^2+ml\dot{\varphi}\dot{x}-\frac{1}{2}mgl\varphi^2\ .\]
Nápověda – rovnice
Lagrangeovy rovnice II. druhu mají tvar:

\[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial L}{\partial \dot{q}_{j}}\right)-\frac{\partial L}{\partial {q}_{j}} = 0,\] pro j = 1, 2 ... n,

kde q_j je j-tá zobecněná souřadnice hmotného bodu a L Lagrangeova funkce.

Dosaďte do tohoto předpisu lagrangián aproximovaný pro malé kmity a rychlosti pohybu kyvadla.
Řešení nápovědy
Nejprve si nachytáme potřebné derivace:
\[\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial \tilde{L}}{\partial\dot{\varphi}} = \frac{\mathrm{d}}{\mathrm{d}t}(ml^2\dot{\varphi}+ ml\dot{x}) = ml^2\ddot{\varphi}+ ml\ddot{x}\] \[\frac{\partial \tilde{L}}{\partial \varphi} = -mgl\varphi\] \[\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial \tilde{L}}{\partial\dot{x}} = \frac{\mathrm{d}}{\mathrm{d}t}\left[(M+m)\dot{x} + ml\dot{\varphi}\right] = (M+m)\ddot{x} + ml\ddot{\varphi}\] \[\frac{\partial \tilde{L}}{\partial x} = 0\]
a pomocí nich sestavíme rovnice:
\[ml^2\ddot{\varphi}+ ml\ddot{x} + mgl\varphi = 0\] \[(M+m)\ddot{x} + ml\ddot{\varphi} = 0\]
Můžeme upravit:
\[l\ddot{\varphi} + \ddot{x} + g\varphi = 0\tag{1}\] \[\ddot{x} = -\frac{m}{M+m}l\ddot{\varphi}\tag{2}\]
A dosadit z (2) do (1):
\[l\ddot{\varphi} -\frac{m}{M+m}l\ddot{\varphi} + g\varphi = 0\] \[\ddot{\varphi} + \frac{M+m}{M}\frac{g}{l}\varphi = 0\]
Poslední vztah je zřejmě pohybová rovnice lineárního harmonického oscilátoru (viz např. úloha Jednorozměrný harmonický oscilátor).
Řešení rovnic
Z lagrangiánu pro malé kmity dosazeného do předpisu Lagrangeových rovnic II. druhu dostáváme vztahy:
\[ml^2\ddot{\varphi}+ ml\ddot{x} + mgl\varphi = 0\] \[(M+m)\ddot{x} + ml\ddot{\varphi} = 0\ ,\]
po úpravě:
\[l\ddot{\varphi} + \ddot{x} + g\varphi = 0\tag{3}\] \[\ddot{x} = -\frac{m}{M+m}l\ddot{\varphi}\ .\tag{4}\]
Dosadíme z (4) do (3) a upravíme:
\[\ddot{\varphi} + \frac{M+m}{M}\frac{g}{l}\varphi = 0\ .\]
Toto je rovnice lineárního harmonického oscilátoru s úhlovou frekvencí ω (viz např. úloha Jednorozměrný harmonický oscilátor):
\[\omega = \sqrt{\frac{M+m}{M}}\sqrt{\frac{g}{l}}\]
Pro zobecněnou souřadnici φ můžeme tedy rovnou psát řešení ve tvaru:
\[\varphi = A \cos \left(\sqrt{\frac{M+m}{M}}\sqrt{\frac{g}{l}}t + \varphi_0\right)\ .\]
Nyní máme časový průběh pohybu závaží a jeho pomocí dopočítáme časový průběh pohybu vozíku. Použijeme rovnici (2).

Budeme počítat s jednodušším zápisem:
\[\varphi = A \cos (\omega t + \varphi_0)\ .\]
Dvakrát zderivujeme podle času:
\[\ddot{\varphi} = -\omega^2A\cos (\omega t + \varphi_0)\]
a dosadíme do (2):
\[\ddot{x} = \omega^2\frac{m}{M+m}lA\cos(\omega t + \varphi_0)\ .\]
Po dosazení za ω v amplitudě a úpravě:
\[\ddot{x} = \frac{m}{M}gA\cos(\omega t + \varphi_0)\ .\]
Po dvojím zintegrování podle času:
\[x = -\frac{1}{\omega^2}\frac{m}{M}gA\cos(\omega t + \varphi_0) + C_1 t +C_2\ .\]
Po dosazení za ω a úpravě:
\[x = -\frac{m}{m+M}lA\cos\left(\sqrt{\frac{M+m}{M}}\sqrt{\frac{g}{l}}t + \varphi_0\right) + C_1 t + C_2\ ,\]
kde integrační konstanty C₁, C₂ lze dopočítat z počáteční rychlosti v₀ a počáteční polohy x₀ vzhledem k souřadnici x.

Získaný vztah pro polohu vozíku x nám říká, že vozíček bude kmitat opačným směrem než kyvadlo (kvůli znaménku minus u prvního členu). Toto kmitání může být složeno s rovnoměrným pohybem, tj. půjde o „trhaný“ pohyb ve směru počáteční rychlosti.
Odpověď
Lagrangián vozíku s kyvadlem je:
\[L = \frac{1}{2}(M+m)\dot{x}^2 + \frac{1}{2}ml^2\dot{\varphi}^2 + ml\dot{\varphi}\dot{x}\cos\varphi + mgl\cos\varphi\ ,\]
kde φ je okamžitá výchylka kyvadla měřená od svislé osy a x je poloha vozíčku na podložce.

Při přiblížení pro malé kmity a rychlosti pohybu kyvadla dostáváme lagrangián ve tvaru:
\[\tilde{L} = \frac{1}{2}(M+m)\dot{x}^2+\frac{1}{2}ml^2\dot{\varphi}^2+ml\dot{\varphi}\dot{x}-\frac{1}{2}mgl\varphi\ .\]
Řešením Lagrangeových rovnic jsme dospěli k rovnicím polohy vozíčku a kyvadla:
\[x = -\frac{m}{m+M}lA\cos\left(\sqrt{\frac{M+m}{M}}\sqrt{\frac{g}{l}}t + \varphi_0\right) + C_{1}t + C_2\ ,\] \[\varphi = A \cos \left(\sqrt{\frac{M+m}{M}}\sqrt{\frac{g}{l}}t + \varphi_0\right)\ .\]
Kmity kyvadla a periodický pohyb vozíčku probíhají v protifázi. Kmitání vozíčku může být složeno s jeho rovnoměrným pohybem, záleží na počáteční rychlosti vozíčku (zda odopovídá pouze kmitání nebo část odpovídá i rovnoměrnému pohybu).

Ze skutečnosti, že kmity kyvadla a vozíku probíhají v protifázi by se dalo usuzovat, že se zde nějakým způsobem projevuje zachování hybnosti. Blíže je tato vlastnost komentována v úloze První integrály Lagrangeových rovnic.
Komentář – zvláštní případy pro velmi rozdílné hmotnosti
Jako jistá kontrola správnosti nám může sloužit, že pokud bude hmotnost kyvadla m oproti hmotnosti vozíčku M zanedbatelná, dostaneme pohybové rovnice:
\[x = v_{0}t + x_0\] \[\varphi = A \cos \left({\sqrt{\frac{g}{l}}}t + \varphi_0\right)\]
Kyvadlo se tedy bude chovat jako matematické kyvadlo, jehož závěs je pevně uchycen a pohyb kyvadla nebude pohyb vozíčku nijak ovlivňovat. V praxi bychom tento speciální případ mohli ilustrovat třeba na vagónu uhlí, na kterém je přichycen kývající se pingpongový míček. Pro míček je vagón de facto nepohyblivým pevným bodem uchycení a na druhé straně kývání míčku vagón uhlí skutečně neovlivní.

V opačném případě, tedy zanedbatelně malé hmotnosti vozíčku oproti hmotnosti kyvadla, poroste nade všechny meze jak úhlová frekvence kývání kyvadla, tak amplituda periodického pohybu vozíčku. Přesně dopočítat tento případ ovšem není z lagrangiánu \(\tilde{L}\) logicky možné, protože tento byl aproximován pro malé rychlosti pohybu kyvadla.
Komentář – integrační konstanty
Řešili jsme soustavu dvou diferenciálních rovnic II. řádu. Teorie tedy říká, že by v jejich řešení měly být obsaženy 4 integrační konstanty – dvě za každou rovnici, protože řešení diferenciální rovnice II. řádu v sobě principielně dvakrát ukrývá integrování.

Můžeme se přesvědčit, že tomu tak skutečně je. Integračními konstantami jsou veličiny o fyzikálním významu amplitudy kývání kyvadla A, jeho počáteční fáze φ₀, počáteční rychlosti vozíčku v₀ a počáteční polohy vozíčku x₀.

Je zřejmé, že tato čtveřice musí být zadána, resp. dopočítána z počátečních podmínek.