Špageta na nakloněných rovinách

Úloha číslo: 1055

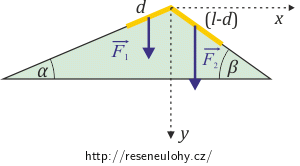
Na hraně dvou nakloněných rovin (v řezu viz obrázek) je položena dokonale kluzká a ohebná špageta délky l. Určete její rovnovážnou polohu v závislosti na úhlech α a β.

Nápověda 1
Nejprve si rozmyslete, které síly na špagetu působí, zapište je a zakreslete do obrázku.
Řešení nápovědy 1
Na špagetu působí jediná vtištěná síla, a to síla tíhová. Špagetu můžeme rozdělit podle hrany nakloněných rovin na dvě části. Oběma částem přisoudíme tíhové síly, které umístíme do těžišť jednotlivých částí.

Tíhové síly působí vzhledem k zavedení souřadnic (viz obrázek) ve směru osy y. Velikosti tíhových sil vyjádříme pomocí lineární hustoty τ špagety, její délky l, délky d jedné části špagety a tíhového zrychlení g:
\[F_1=\tau dg,\] \[F_2=\tau (l-d)g.\]
Nápověda 2
Napište zobecněný princip virtuální práce a uvědomte si, která virtuální posunutí potřebujete znát.
Řešení nápovědy 2
Zobecněný princip virtuální práce zní obecně takto:
\[\sum_{i=1}^N \vec{F_i}\cdot\delta\vec{r_i}=0,\]
kde \(\vec{F_i}\) jsou výslednice vtištěných sil na i-tý hmotný bod a \(\vec{r_i}\) jsou virtuální posunutí slučitelná s vazbami i-tého hmotného bodu.

Vzhledem k tomu, že x-ové složky sil působících na obě časti jsou nulové, nemusíme uvažovat členy, obsahující posunutí v tomto směru. Zobecněný princip virtuální práce tak bude mít pouze dva členy:
\[F_1\delta y_1+F_2\delta y_2=0.\tag{1}\]
Nápověda 3
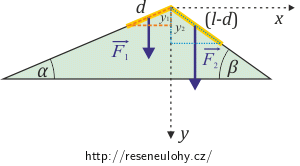
Ve vyjádření zobecněného principu virtuální práce z předchozí nápovědy zatím neznáme virtuální posunutí těžišť obou částí špagety. Aby bylo možné napsat vratná virtuální posunutí slučitelná s vazbami, je třeba nejprve znát vyjádření souřadnic těžišť v závislosti na parametru, jehož hodnota nebude omezena vazbovými podmínkami. Rozmyslete si volbu tohoto parametru, pomocí něho vyjádřete souřadnice těžišť obou částí špagety a jejich virtuální posunutí.
Řešení nápovědy 3 – vyjádření souřadnic
Při klouzání špagety po rozhraní nakloněných rovin se bude měnit délka obou částí špagety. Tuto změnu nám popisuje změna délky části špagety d. Jelikož hodnota délky d není omezena vazbovými podmínkami, zvolíme ji jako parametr. Tento parametr popisuje obě části špagety, takže úloha má jen jeden stupeň volnosti. Pomocí parametru d tedy vyjádříme souřadnice těžišť obou kusů špagety. K tomu využijeme pravoúhlých trojúhelníků naznačených na obrázku:
\[y_1=\frac{d}{2}\sin{\alpha},\] \[y_2=\frac{l-d}{2}\sin{\beta},\]
kde y₁ a y₂ jsou y-ové souřadnice těžišť jednotlivých kusů špagety.
Řešení nápovědy 3 – virtuální posunutí
Vyjádřeme virtuální posunutí v závislosti na proměnné d. Obecně bude platit:
\[\delta y=\frac{\mathrm{d}y}{\mathrm{d}d}\delta d.\]
Spočteme-li derivace a dosadíme, získáme:
\[\delta y_1=\frac{1}{2}\sin{(\alpha)}\,\delta d,\] \[\delta y_2=-\frac{1}{2}\sin{(\beta)}\,\delta d.\]
Nápověda 4
Dosaďte do vyjádření zobecněného principu virtuální práce za vtištěné síly a vratná virtuální posunutí slučitelná s vazbami a napište podmínku rovnováhy špagety na nakloněných rovinách. (Vyjádření vtištěných sil naleznete v nápovědě 1 a vratná viruální posunutí slučitelná s vazbami v nápovědě 3.)
Řešení nápovědy 4
Dosazujeme do rovnice (1), kterou jsme odvodili ve tvaru:
\[F_1\delta y_1+F_2\delta y_2=0.\tag{1}\]
Tedy:
\[\frac{1}{2}\tau dg \sin{(\alpha)}\,\delta d-\frac{1}{2}\tau(l-d)g \sin{(\beta)}\,\delta d=\frac{1}{2}\tau g(d \sin{\alpha}-l \sin{\beta}+d \sin{\beta})\,\delta d=0.\]
Výraz před poslední rovností je roven nule právě tehdy, když je závorka rovna nule. Tedy:
\[d \sin{\alpha}-l \sin{\beta}+d \sin{\beta}=0.\]
Z toho plyne vyjádření pro d:
\[d=\frac{l \sin{\beta}}{\sin{\alpha}+\sin{\beta}}.\]
Špageta délky l je tedy v rovnováze, pokud část, která leží na rovině s úhlem α, má výše uvedenou délku d.
Celkové řešení
Úlohu řešíme za pomoci zobecněného principu virtuální práce, který má obecný tvar:
\[\sum_{i=1}^N \vec{F_i}\cdot\delta\vec{r_i}=0,\]
kde \(\vec{F_i}\) jsou výslednice vtištěných sil na i-tý hmotný bod a \(\vec{r_i}\) jsou virtuální posunutí slučitelná s vazbami i-tého hmotného bodu.

Rozmyslíme si, jaké vtištěné síly působí na špagetu (viz nápověda 1). V našem případě nabývá zobecněný princip virtuální práce tvaru:
\[F_1\delta y_1+F_2\delta y_2=0,\tag{1}\]
kde F₁ a F₂ jsou velikosti tíhových sil působící na jednotlivé části špagety a \(\delta y_1\) a \(\delta y_2\) jsou vratná virtuální posunutí ve směru osy y těžišť obou částí špagety slučitelná s vazbami.

Velikosti sil jsme v nápovědě 1 vyjádřili takto:
\[F_1=\tau dg,\] \[F_2=\tau (l-d)g.\]
Virtuální posunutí vyjádříme v závislosti na parametru d, jehož velikost je nezávislá na vazbách. (Podrobnější diskuzi naleznete v nápovědě 3.):
\[\delta y_1=\frac{1}{2}\sin{(\alpha)}\,\delta d,\] \[\delta y_2=-\frac{1}{2}\sin{(\beta)}\,\delta d.\]
Nyní stačí dosadit do rovnice (1) za všechny příslušné veličiny.

Získáme tak rovnici:
\[\frac{1}{2}\tau dg \sin{(\alpha)}\,\delta d-\frac{1}{2}\tau(l-d)g \sin{(\beta)}\,\delta d= \frac{1}{2}\tau g(d \sin{\alpha}-l \sin{\beta}+d \sin{\beta})\,\delta d=0.\]
Výraz před poslední rovností je roven nule právě tehdy, když je závorka rovna nule. Tedy:
\[d \sin{\alpha}-l \sin{\beta}+d \sin{\beta}=0.\]
Z toho plyne vyjádření pro d:
\[d=\frac{l \sin{\beta}}{\sin{\alpha}+\sin{\beta}}.\]
Špageta délky l je tedy v rovnováze, pokud část, která leží na rovině s úhlem α, má výše uvedenou délku d.
Odpověď
Špageta délky l je v rovnovážné poloze, pokud část, která leží na rovině s úhlem α, má délku d danou výrazem:
\[d=\frac{l \sin{\beta}}{\sin{\alpha}+\sin{\beta}}.\]

Špageta na nakloněných rovinách

Úloha číslo: 1055

Nápověda 1

Řešení nápovědy 1

Nápověda 2

Řešení nápovědy 2

Nápověda 3

Řešení nápovědy 3 – vyjádření souřadnic

Řešení nápovědy 3 – virtuální posunutí

Nápověda 4

Řešení nápovědy 4

Celkové řešení

Odpověď