Sbírka řešených úloh

Fyzické kyvadlo

Úloha číslo: 674

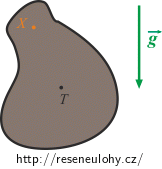
Tuhé těleso o hmotnosti m má těžiště v bodě T. Jeho pohyb je omezen pevnou osou procházející bodem X kolmo k rovině náčrtku. Těleso po ose nemůže klouzat. Napište lagrangián jeho pohybu, sestavte a vyřešte Lagrangeovy rovnice II. druhu při aproximaci malých kmitů.

Moment setrvačnosti tuhého tělesa vzhledem k ose procházející bodem X označte J.

• Nápověda 1

  Kolik stupňů volnosti má tuhé těleso obecně? Kolik jich zbude, pokud jeho pohyb omezíme tak, jak je uvedeno v zadání?

• Řešení nápovědy 1

  Tuhé těleso má obecně až 6 stupňů volnosti. Může vykonávat translační pohyb ve směru všech tří os a kolem každé z nich může i rotovat. K popisu jeho polohy tedy potřebujeme 6 údajů (například kartézské souřadnice těžiště a tři úhly natočení).

  Uchycením na pevnou osu tělesu zabráníme v jakémkoli posuvném pohybu a ze tří možných rotací zbude jen jediná. K popisu polohy tuhého tělesa na pevné ose tedy stačí jen jediný údaj – jeden úhel.

• Nápověda 2

  Rozmyslete, které veličiny bude potřeba „přečíst“ z geometrie systému, a vhodně zvolte zobecněné souřadnice.

• Řešení nápovědy 2

  Vzdálenost |XT| označme l. Za zobecněnou souřadnici zvolíme úhel φ, který svírá úsečka XT se svislým směrem.

  

• Nápověda 3

  Určete kinetickou energii tuhého tělesa. Ta je obecně určena Königovou větou. Jak bude vypadat v tomto případě?

• Řešení nápovědy 3

  Königova věta říká, že kinetická energie tuhého tělesa je dána vztahem:

  \[T = \frac{1}{2}mv^2+\frac{1}{2}J\omega^2\ ,\]

  tj., že celkovou kinetickou energii dostaneme jako součet kinetické energie rotačního a translačního pohybu.

  Vzhledem k tomu, že naše těleso nemůže vykonávat posuvný pohyb, zbude pouze druhý člen. Do něj dosadíme vztah mezi úhlovou rychlostí a zobecněnou souřadnicí φ:

  \[\omega = \dot{\varphi}\ ,\]

  tedy:

  \[T = \frac{1}{2}J\dot{\varphi}^2\ .\]

• Nápověda 4

  Jak bude vypadat potenciální energie tuhého tělesa, které se otáčí na ose? Projděte si určení potenciální energie v úloze Matematické kyvadlo a zjistěte, jak je potřeba tento postup pozměnit pro případ tuhého tělesa.

• Řešení nápovědy 4

  Není potřeba uvažovat potenciální energii každého kousíčku tělesa. Potenciální energie tělesa v homogenním tíhovém poli je stejná jako energie hmotného bodu o celkové hmotnosti tělesa, umístěného v těžišti.

  Provedeme-li tuto úvahu, můžeme nadále postupovat stejně jako u matematického kyvadla. Potenciální energie je tedy rovna:

  \[V = -mgl\cos \varphi.\]

• Řešení – lagrangián

  Fyzické kyvadlo má jen jeden stupeň volnosti, takže k popisu jeho pohybu stačí jediná zobecněná souřadnice.

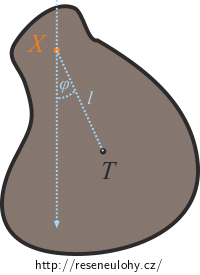
  Vzdálenost |XT| označme l. Za zobecněnou souřadnici zvolíme úhel φ, který svírá úsečka XT se svislým směrem.

  

  Kinetickou energii tuhého tělesa uchyceného na ose spočteme podle vzorce:

  \[T = \frac{1}{2}J\omega^2\ ,\]

  do kterého za úhlovou rychlost ω dosadíme derivaci zobecněné souřadnice φ:

  \[T = \frac{1}{2}J\dot{\varphi}^2\ .\]

  Uvědomíme-li si, že potenciální energie tělesa je stejná jako potenciální energie hmotného bodu o celkové hmotnosti tělesa, který je umístěn v těžišti, pak potenciální energii určíme podobně jako u matematického kyvadla:

  \[V = -mgl\cos \varphi\ .\]

  Odtud sestavíme lagrangián:

  \[L = \frac{1}{2}J\dot{\varphi}^2 + mgl\cos \varphi\ .\]

• Nápověda 5

  Obecný tvar Lagrangeových rovnic II. druhu je:

  \[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial L}{\partial \dot{q}_{j}}\right)-\frac{\partial L}{\partial {q}_{j}} = 0,\] pro j = 1, 2 ... n

  Aproximaci pro malé kmity udělejte pomocí přibližného vzorce pro malá φ:

  \[\sin \varphi \approx \varphi.\]

• Řešení – Lagrangeova rovnice

  Připravíme si derivace Lagrangeovy funkce:

  \[\frac{\partial L}{\partial \dot{\varphi}} = J\dot{\varphi}\] \[\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial L}{\partial \dot{\varphi}} = J\ddot{\varphi}\] \[\frac{\partial L}{\partial \varphi}=-mgl\sin \varphi\ .\]

  Lagrangeova rovnice tedy zní:

  \[J\ddot{\varphi} + mgl\sin \varphi = 0\]

  a po úpravě:

  \[\ddot{\varphi} + \frac{mgl}{J}\sin \varphi = 0\ .\]

  Použijeme přibližný vzorec pro malá φ:

  \[\sin \varphi \approx \varphi\ .\]

  Jeho použitím dostáváme linearizovanou rovnici:

  \[\ddot{\varphi} + \frac{mgl}{J}\varphi = 0\ ,\]

  kterou řeší funkce:

  \[\varphi = A\cos\left(\sqrt{\frac{mgl}{J}} t + \varphi_0\right) \ ,\]

  kde A je amplituda výchylky a φ₀ počáteční fáze.

• Odpověď

  Lagrangián fyzického kyvadla je:

  \[L = \frac{1}{2}J\dot{\varphi}^2 + mgl\cos \varphi\ .\]

  Řešením pohybových rovnic pro malé kmity je funkce:

  \[\varphi = A\sin\left(\sqrt{\frac{mgl}{J}} t + \varphi_0\right)\ ,\]

  kde A je amplituda výchylky, φ₀ počáteční fáze a l vzdálenost těžiště od osy |XT|.

• Komentář – rychlá kontrola

  Správnost výsledku je možné alespoň přibližně ověřit dosazením momentu setrvačnosti hmotného bodu pohybujícího se v konstantní vzdálenosti l od osy rotace, tedy matematického kyvadla:

  \[J_{\mathrm{mat. kyv.}} = ml^2\]

  a jeho dosazením do lagrangiánu i funkce popisující kmity. Výsledek srovnejte s výsledky úlohy Matematické kyvadlo.