Závaží na dvou nakloněných rovinách
Úloha číslo: 1248
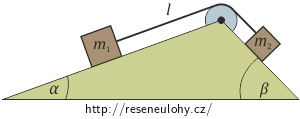
Pomocí Hamiltonových kanonických rovnic najděte zrychlení, se kterým se pohybuje závaží o hmotnosti m1, které klouže po boční stěně nepohyblivého hranolu se sklonem α a je spojeno přes kladku o poloměru R se závažím o hmotnosti m2 na stěně o sklonu β (viz obrázek). Tření a hmotnost kladky zanedbejte. Nakreslete fázovou dráhu závaží ve fázovém prostoru.
Nápověda 1
Rozmyslete si, kolik stupňů volnosti má zkoumaný systém, a vhodně zvolte zobecněné souřadnice, pomocí kterých budete úlohu řešit.
Vyjádřete potenciální energii V a kinetickou energii T systému. Tato vyjádření budete potřebovat pro sestavení hamiltoniánu H.
Nápověda 2
Všimněte si, že vyjádření kinetické energie T a potenciální energie V nejsou explicitně závislá na čase. V takovém případě můžeme Hamiltonovu funkci H sestavit jako celkovou mechanickou energii. Proveďte.
Hamiltonovu funkci H vyjadřujeme v jejich přirozených proměnných, kterými jsou zobecněné souřadnice a hybnosti. Pro vyjádření zobecněných hybností je zapotřebí napsat Lagrangeovu funkci L. Zobecněné hybnosti pak získáme podle vztahu:
\[p_i=\frac{\partial{L}}{\partial{\dot{q_i}}},\]kde qi jsou zobecněné souřadnice a pi jsou příslušné zobecněné hybnosti.
Nápověda 3
Napište Hamiltonovy kanonické rovnice a vyjádřete zrychlení systému.
Hamiltonovy kanonické rovnice mají obecně tvar:
\[\dot{q_i}=\frac{\partial{H}}{\partial{p_i}},\] \[\dot{p_i}=-\frac{\partial{H}}{\partial{q_i}},\] \[\frac{\partial{L}}{\partial{t}}=-\frac{\partial{H}}{\partial{t}}.\]Jelikož hamiltonián H a lagrangián L nejsou explicitně závislé na čase, je poslední uvedená rovnice automaticky splněna.
Nápověda 4
Určete trajektorii systému ve fázovém prostoru – vyjádřete závislost souřadnice x na hybnosti p. V této úloze je vhodným postupem určit časový vývoj souřadnice x a hybnosti p. Abyste jej zjistili, využijte zrychlení systému, které jste spočítali v předchozím oddíle.
Speciální případy volby úhlů
Jak již bylo řečeno, úhly α a β dosazujeme v radiánech. Jelikož jsou úhly α a β vnitřními úhly trojúhelníku a zároveň to jsou úhly ostré (v opačném případě by již obě závaží nemohla ležet na nakloněných rovinách), mohou nabývat hodnot pouze v intervalu [0;π/2]. Podívejme se na mezní případ:
\[\alpha=\beta=\frac{\pi}{2}.\]Jedná se vlastně o dvě provázkem spojená závaží, která volně visí na kladce.
V takovém případě získáme zrychlení ve tvaru:
\[\ddot{x}=\frac{m_1-m_2}{m_1+m_2}g,\]což odpovídá výsledkům úlohy Hmotná kladka.
Druhý mezní případ je:
\[\alpha=\beta=0.\]V takovém případě by se jednalo o dvě závaží, která leží na vodorovné rovině, a jejich zrychlení by tedy bylo nulové.
Pokud by nás zajímala symetrická situace
\[\alpha=\beta ,\]získali bychom rovnici pro zrychlení ve tvaru:
\[\ddot{x}=\frac{m_1-m_2}{m_1+m_2}g\sin{\alpha}.\]Celkové řešení
Úloha má pouze jeden stupeň volnosti. Pomocí souřadnic x a y, které vidíte na obrázku, určíme polohy záváží.
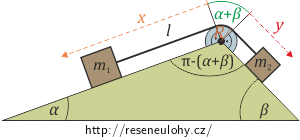
Provázek má délku:
\[l=x+y+(\alpha +\beta)R.\]Pro y tak platí podmínka:
\[y=l-(\alpha+\beta)R-x.\]Za souřadnici y budeme toto vyjádření v dalších výpočtech dosazovat. Souřadnice x bude tedy jedinou (zobecněnou) souřadnicí popisující náš systém.
S pomocí délky provázku tak můžeme vyjádřit časovou derivaci souřadnice y:
\[\dot{y}=\frac{\mathrm{d}}{\mathrm{d}t}(l-(\alpha+\beta)R-x)=-\dot{x}.\]Nyní již můžeme vyjádřit kinetickou energii T. Ta má dvě složky odpovídající kinetickým energiím posuvného pohybu jednotlivých závaží:
\[T=T_1+T_2=\frac{1}{2}m_1\dot{x}^2+\frac{1}{2}m_2\dot{y}^2=\frac{1}{2}m_1\dot{x}^2+\frac{1}{2}m_2(-\dot{x})^2=\frac{1}{2}(m_1+m_2)\dot{x}^2.\]Stejně tak bude mít i potenciální energie V dvě složky odpovídající tíhovým potenciálním energiím jednotlivých závaží:
\[V=V_1+V_2=-m_1gx\sin{\alpha}+m_2gx\sin{\beta}+K,\]kde K označuje konstantní členy potenciální energie vzniklé při dosazení za souřadnici y.
Kinetická a potenciální energie nejsou explicitně závislé na čase, proto můžeme sestrojit hamiltonián H jako celkovou mechanickou energii. Přirozenými proměnnými hamiltoniánu H jsou zobecněné souřadnice a zobecněné hybnosti. Zobecněnou hybnost p získáme jako:
\[p=\frac{\partial{L}}{\partial{\dot{x}}}=(m_1+m_2)\dot{x},\]kde L je Lagrangeova funkce definovaná vztahem:
\[L=T-V.\]Pro Hamiltonovu funkci H tak můžeme psát vyjádření:
\[H=T+V=\frac{p^2}{2(m_1+m_2)}-m_1gx\sin{\alpha}+m_2gx\sin{\beta}+K.\]Hamiltonovy kanonické rovnice v našem případě nabývají tvaru:
\[\dot{x}=\frac{\partial{H}}{\partial{p}}=\frac{p}{m_1+m_2},\] \[\dot{p}=-\frac{\partial{H}}{\partial{x}}=m_1g\sin{\alpha}-m_2g\sin{\beta}.\]Hledané zrychlení \(\ddot{x}\) dostaneme zderivováním první rovnice a dosazením za \(\dot{p}\) z druhé rovnice. Zrychlení je konstantní, proto jej označíme jako a:
\[\ddot{x}=\frac{m_1\sin{\alpha}-m_2\sin{\beta}}{m_1+m_2}g=a.\]Trajektorii pohybu ve fázovém prostoru určíme z časového vývoje souřadnice x a hybnosti p. Souřadnici x můžeme vyjádřit dvojí integrací vztahu pro zrychlení:
\[\dot{x}=at+v_0,\] \[x=\frac{1}{2}at^2+v_0t+x_0,\]kde v0 je počáteční rychlost a x0 počáteční výchylka.
Podrobněji viz nápověda 4.
Hybnost p získáme dosazením:
\[p=(m_1+m_2)\dot{x}=(m_1+m_2)(at+v_0).\]Pro získání trajektorie musíme určit závislost x a p vyloučením času t. Vyjádříme tedy ze vztahu pro hybnost čas t:
\[t=\frac{p-(m_1+m_2)v_0}{a(m_1+m_2)}.\]Nyní můžeme dosadit do vyjádření souřadnice x za čas t a po úpravě dostaneme:
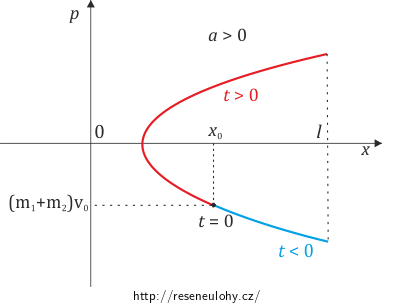
\[x=\frac{p^2}{2a(m_1+m_2)^2}-\frac{v_0^2}{2a}+x_0.\]Můžeme tak nakreslit graf trajektorie ve fázovém prostoru, kterou je parabola.
Obrázek je nakreslen pro zrychlení a > 0, které míří ve směru osy x. Počáteční rychlost v0 je naopak záporná, a tedy míří proti směru osy x. Závaží m1 se proto vlivem udělené počáteční rychlosti nejprve posouvá směrem vzhůru po nakloněné rovině a poté začne klesat směrem dolů. Tento pohyb odpovídá červené části grafu pro čas t > 0.
Pohybové rovnice lze řešit i pro čas t < 0. Tato řešení odpovídají vývoji systému, než jsme začali měřit čas. V grafu znázorněno modře.
Souřadnici x jsme zavedli tak, že může nabývat pouze kladných hodnot, hybnost p však závisí na časové změně souřadnice x, proto může být i záporná.
Znaménko zrychlení a rozhoduje o tom, zda bude parabola otočena doprava, jako je tomu na obrázku, nebo doleva. V případě otočení doleva by parabola končila tak, aby nepřesáhla do záporných hodnot souřadnice x. V takovém případě by již závaží m1 neleželo na nakloněné rovině. Stejně tak při kladném zrychlení je parabola ukončena pro x = l, což odpovídá hraniční situaci, kdy se závaží m2 nachází na samotném rozhraní nakloněných rovin.
Odpověď
Hamiltonova funkce H má vyjádření:
\[H=\frac{p^2}{2(m_1+m_2)}-m_1gx\sin{\alpha}+m_2gx\sin{\beta}+K.\]Hamiltonovy kanonické rovnice mají tvar:
\[\dot{x}=\frac{p}{m_1+m_2},\] \[\dot{p}=m_1g\sin{\alpha}-m_2g\sin{\beta}.\]Zrychlení systému je:
\[\ddot{x}=\frac{m_1\sin{\alpha}-m_2\sin{\beta}}{m_1+m_2}g.\]Trajektorie pohybu ve fázovém prostoru je parabola daná rovnicí:
\[x=\frac{p^2}{2a(m_1+m_2)}-\frac{v_0^2}{2a}+x_0.\]Hmotná kladka
V případě, že by kladka měla nenulovou hmotnost M, objevil by se ve vyjádření kinetické energie dodatečný člen Tk:
\[T_k=\frac{1}{4}M\dot{x}^2.\]To by se projevilo zmenšením výsledného zrychlení, kde by se ve jmenovateli objevil člen odpovídající hmotnosti kladky M:
\[\ddot{x}=\frac{m_1\sin{\alpha}-m_2\sin{\beta}}{m_1+m_2+\frac{1}{2}M}g.\]Ve speciálním případě volby úhlů α = π/2 a β = π/2 odpovídá tento vztah výsledku úlohy Hmotná kladka.