Těžiště půlválce se závažím
Úloha číslo: 2165
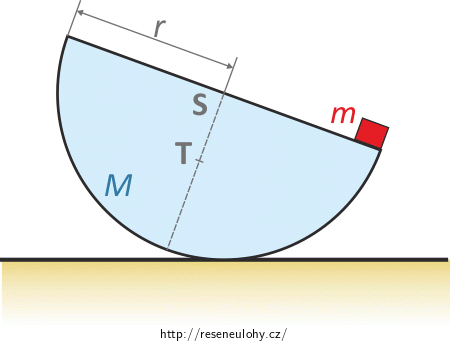
Nalezněte rovnovážnou polohu homogenního půlválce o hmotnosti \(M\) a poloměru \(r\), na jehož jednom konci je položeno závažíčko o hmotnosti \(m\). (Těžiště půlválce se nachází ve vzdálenosti \(\frac {4r}{3π}\) od bodu \(S\).) Rozměry závažíčka považujte za zanedbatelné.
Nápověda 1
K řešení užijte zobecněný princip virtuální práce.
Nápověda 2
Nejprve si rozmyslíme, jaké aktivní síly na soustavu působí, zakreslíme je do obrázku a zvolíme si soustavu souřadnou.
Nápověda 3
Určeme souřadnice těžiště T a závažíčka X vzhledem k námi dané soustavě souřadnic v závislosti na úhlu odklonu \(\alpha\) osy půlválce od osy \(y\).
Kompletní řešení
Nejprve si rozmyslíme, jaké aktivní síly působí, zakreslíme je do obrázku a zvolíme si soustavu souřadnou.
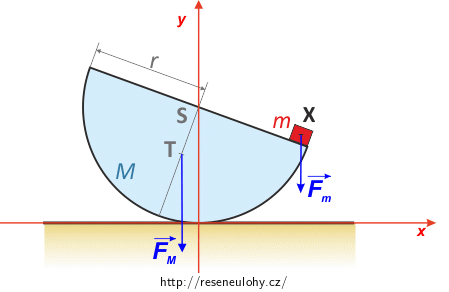
Na půlválec o hmotnosti \(M\) působí tíhová síla \(\vec {F_M}\) s působištěm v jeho těžišti T a na malou kostičku o hmotnosti \(m\) působí tíhová síla \(\vec {F_m}\) v bodě X. Soustavu souřadnic si můžeme zvolit vcelku libovolně, ovšem pro jednoduchost zvolme soustavu souřadnic tak jako na obrázku.
Určeme souřadnice těžiště T a závažíčka X vzhledem k námi dané soustavě souřadnic v závislosti na úhlu odklonu \(\alpha\) osy půlválce od osy \(y\).
Nejprve si do obrázku zakreslíme náš úhel \(\alpha\).
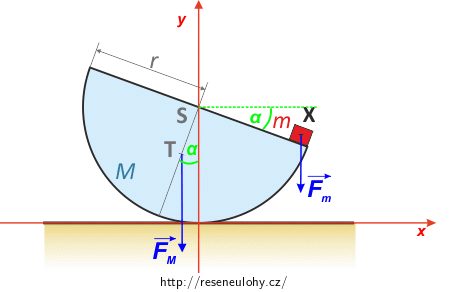
Podívejme se na souřadnice bodů X a T v naší soustavě souřadnic.
Pomocí goniometrických vztahů dostaneme pro bod T:
\[ x_T=-\frac {4r}{3\pi}\, \sin{\alpha} \] \[ y_T=r-\frac {4r}{3\pi}\, \cos{\alpha} \]A velmi podobně pro bod X dostaneme:
\[ x_X=r\, \cos{\alpha} \] \[ y_X=r-r\, \sin{\alpha} \]Chceme určit polohu těžiště T v rovnovážné poloze. Víme, že v rovnovážné poloze platí, že výslednice všech sil působícíh na těleso je nulová. Z této podmínky vychází princip virtuální práce, jež užijeme k řešení úlohy. Zobecněný princip virtuální práce (ZPVP) pro soustavu \(N\) hmotných bodů říká, že pro libovolná virtuální posunutí \(\delta \vec {r_i}\) platí, že virtuální práce aktivních sil působících na soustavu pro tato virtuální posunutí je nulová, tedy:
\[\delta W=\sum_{i=1}^N {\vec {F_i} \cdot \delta \vec {r_i}}=0\]Tedy budeme pro výpočet potřebovat vyjádřit naše virtuální posunutí i naše aktivní síly. Začněme tím jednodušším, tedy silami. V naší soustavě platí:
\[\vec {F_M}=(0;\,-Mg)\] \[\vec {F_m}=(0;\,-mg)\]Virtuální posunutí mohou být i nekonečně malá a chovají se jako diferenciály. Jelikož naše těžiště \(T\) je jednoznačně určeno úhlem \(\alpha\), považujme \(\alpha\) za naši zobecněnou souřadnici a daná virtuální posunutí určeme jako:
\[\delta \vec {r_i}=\frac {\mathrm{d}\vec {r_i}}{\mathrm{d}\alpha}\, \delta\alpha\]Tedy bude platit:
\[ \delta x_T=-\frac {4r}{3\pi}\, \cos{\alpha}\, \delta\alpha\] \[ \delta y_T=\frac {4r}{3\pi}\, \sin{\alpha}\, \delta\alpha\] \[ \delta x_X=-r\, \sin{\alpha}\, \delta \alpha\] \[ \delta y_X=-r\, \cos{\alpha}\, \delta \alpha\]Určeme si tedy naši rovnici pro ZPVP:
\[\sum_{i=1}^N {\vec {F_i} \cdot \delta \vec {r_i}} = \vec{F_M} \cdot \delta\vec{r_T} + \vec{F_m} \cdot \delta\vec{r_X}=\] \[=0\,\delta x_T - Mg\,\delta y_T + 0\,\delta x_X - mg\delta y_X=0\]Tedy po dosazení virtuálních posunutí a vykrácení \(-g\) dostaneme:
\[M\frac{4r}{3\pi}\, \sin{\alpha}\, \delta\alpha - mr\, \cos{\alpha}\, \delta\alpha=0 \,\,\,\,\,\,\,\,\,/\frac{1}{r}\] \[M\frac{4}{3\pi}\, \sin{\alpha}\, \delta\alpha - m\, \cos{\alpha}\, \delta\alpha=0\]Jelikož princip virtuální práce musí platit pro libovolné virtuální posunutí, tedy obecně nenulové, můžeme zde „zkrátit“ i \(\delta\alpha\):
\[M\frac{4}{3\pi}\, \sin{\alpha}\, - m\, \cos{\alpha}=0\] \[M\frac{4}{3\pi}\, \sin{\alpha}\, = m\, \cos{\alpha}\]Dostáváme dvě možnosti, buď \(\sin{\alpha}=0 \,\,=\gt\,\,\alpha=0\), což je případ, kdy pro naše závážíčko platí \(m=0\) a nebo \(\sin{\alpha}\neq 0\), a tedy platí:
\[\frac{4M}{3\pi m} = \mathrm{cotg}\,{\alpha}\] \[\mathrm{arccotg}\,{\frac{4M}{3\pi m}} = \alpha\]Tím jsme se dobrali ke vztahu pro úhel \(\alpha\), který nám již stačí dosadit do rovnic pro \(x_T\) a \(y_T\):
\[x_T= - \frac{4}{3\pi}\, \sin{\left(\mathrm{arccotg}\,{\frac{4M}{3\pi m}}\right)}\] \[y_T=r- \frac{4}{3\pi}\, \cos{\left(\mathrm{arccotg}\,{\frac{4M}{3\pi m}}\right)}\]Odpověď
V námi zvolené soustavě souřadnic (viz. Nápověda 1 – řešení) platí v rovnovážné poloze pro souřadnice \(x_T\) a \(y_T\) těžiště T vztahy:
\[x_T= - \frac{4}{3\pi}\, \sin{\left(\mathrm{arccotg}\,{\frac{4M}{3\pi m}}\right)}\] \[y_T=r- \frac{4}{3\pi}\, \cos{\left(\mathrm{arccotg}\,{\frac{4M}{3\pi m}}\right)}\]

