Sbírka řešených úloh

Tenzor setrvačnosti kvádru

Úloha číslo: 2236

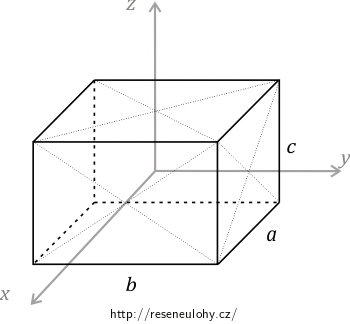
Určete tenzor setrvačnosti homogenního kvádru o stranách s délkou \(a, \, b, \, c\) vzhledem k hmotnému středu kvádru.

Dále určete moment setrvačnosti tohoto kvádru vůči tělesové úhlopříčce.

• Nápověda 1

  Rozmyslete si, s jakými vztahy budete pracovat a které všechny veličiny potřebujete znát pro určení tenzoru setrvačnosti.

• Řešení – Nápověda 1

  Jelikož se jedná o homogenní kvádr, bude vhodné uvažovat vztahy platné pro spojité prostředí. Tedy pro určení jednotlivých složek tenzoru setrvačnosti \(J_{jk}\) platí vztah:

  \[J_{jk}= \int_V {( \delta_{jk} \, r^2 - x_j \, x_k ) \rho} \, \mathrm{d}V,\]

  kde \(r\) je vzdálenost od počátku soustavy, \(\delta_{jk}\) je Kroneckerovo delta a souřadnice polohového vektoru \(x_i\) pro \(i=\) 1 až 3 jsou obecnějším zapsáním našich souřadnic \(x, \, y, \, z\).

  Poznámka: odvození tohoto vztahu viz například: Studijní text k teoretické mechanice tuhého tělesa.

  Potřebujeme znát i hustotu kvádru \(\rho\). Protože je náš kvádr homogenní, je tato hustota konstantní.

• Nápověda 2

  Vypočítejte postupně jednotlivé složky tenzoru a zapište je do matice.

  Rozmyslete si jednotlivé integrační meze a celkovou podobu našeho objemového integrálu.

• Řešení – Nápověda 2

  Určeme nejprve moment setrvačnosti rotace okolo osy \(x\) odpovídajcí složce \(J_{xx}\):

  \[J_{xx}=J_{11}= \int_V {\left ( \delta_{11} \, r^2 - x_1 x_1 \right) \rho} \mathrm{d}V = \int_V {\left ( x^2 + y^2 + z^2 - x^2 \right ) \rho} \mathrm{d}V =\int_V {\left ( y^2 + z^2 \right ) \rho} \mathrm{d}V.\]

  Tento objemový integrál je třeba spočítat jako trojný integrál přes proměnné \(x, \, y\) a \(z\). Jelikož je střed naší soustavy v těžišti kvádru, budeme integrovat od \(- \frac {d}{2}\) po \(\frac {d}{2}\), kde \(d\) je délka příslušné hrany. Také využijeme toho, že hustota \(\rho\) je konstantní a je tudíž možné ji vytknout před integrál.

  \[J_{xx}= \rho \int_{- \frac {c}{2}}^{\frac {c}{2}} \int_{- \frac {b}{2}}^{\frac {b}{2}} \int_{- \frac {a}{2}}^{\frac {a}{2}} {\left ( y^2 + z^2 \right )} \mathrm{d}x \, \mathrm{d}y \, \mathrm{d}z = \rho \int_{- \frac {c}{2}}^{\frac {c}{2}} \int_{- \frac {b}{2}}^{\frac {b}{2}} {\left ( y^2 + z^2 \right ) \left [ x \right ]_{- \frac {a}{2}}^{\frac {a}{2}}} \mathrm{d}y \, \mathrm{d}z =\] \[= a \rho \int_{- \frac {c}{2}}^{\frac {c}{2}} \int_{- \frac {b}{2}}^{\frac {b}{2}} {\left ( y^2 + z^2 \right )} \mathrm{d}y \, \mathrm{d}z = a \rho \int_{- \frac {c}{2}}^{\frac {c}{2}} {\left [ \frac {y^3}{3} + y \, z^2 \right]_{- \frac {b}{2}}^{\frac {b}{2}}} \mathrm{d}z = a \rho \int_{- \frac {c}{2}}^{\frac {c}{2}} {\left ( \frac {2 \, b^3}{24} + b \, z^2 \right)} \mathrm{d}z =\] \[= ab \rho \int_{- \frac {c}{2}}^{\frac {c}{2}} {\left ( \frac {b^2}{12} + z^2 \right)} \mathrm{d}z = ab \rho \left [ \frac {z \, b^2}{12} + \frac {z^3}{3} \right ]_{- \frac {c}{2}}^{\frac {c}{2}} = ab \rho \frac {1}{3} \left [ \frac {z \, b^2}{4} + z^3 \right ]_{- \frac {c}{2}}^{\frac {c}{2}} = ab \rho \frac {1}{3} \left ( \frac {c \, b^2}{4} + \frac {c^3}{4} \right ) = \] \[= \frac {1}{12} abc \rho \left ( b^2 + c^2 \right )\]

  Výraz \(abc \rho\) má význam celkové hmotnosti našeho kvádru, označíme ji \(m\) a potom můžeme první složku tenzoru setrvačnosti zapsat jako:

  \[J_{xx} = \frac {1}{12} m \left ( b^2 + c^2 \right ) .\]

  Pokračujme výpočtem další složky tenzoru a to složky, která má význam momentu setrvačnosti odpovídajícímu rotaci okolo osy \(y\).

  \[J_{yy}=J_{22}= \int_V {\left ( \delta_{22} \, r^2 - x_2 x_2 \right) \rho} \mathrm{d}V = \int_V {\left ( x^2 + y^2 + z^2 - y^2 \right ) \rho} \mathrm{d}V =\int_V {\left ( x^2 + z^2 \right ) \rho} \mathrm{d}V\]

  Dále můžeme postupovat obdobně jako v předchozím případě, nebo si povšimneme, že vztah je velmi obdobný vztahu pro \(J_{xx}\) a lze stejného výsledku dosáhnout i záměnou parametrů pro \(x\) a \(y\):

  \[J_{yy} = \frac {1}{12} m \left ( a^2 + c^2 \right ) .\]

  (Ověření viz Tenzor setrvačnosti kvádru, Komentář k Nápovědě 2)

  Velmi obdobně se popasujeme i se složkou tenzoru \(J_{zz}\):

  \[J_{zz}=J_{33}= \int_V {\left ( \delta_{33} \, r^2 - x_3 x_3 \right) \rho} \mathrm{d}V = \int_V {\left ( x^2 + y^2 + z^2 - z^2 \right ) \rho} \mathrm{d}V =\int_V {\left ( x^2 + y^2 \right ) \rho} \mathrm{d}V.\]

  A dále podobně jako pro \(J_{yy}\) situaci vyřešíme cyklickou záměnou:

  \[J_{zz} = \frac {1}{12} m \left ( a^2 + b^2 \right ) .\]

  Tím jsme vyřešili složky tenzoru, které představují jednotlivé momenty setrvačnosti vůči osám soustavy souřadnic. Nyní se podíváme na deviační momenty a začneme členem \(J_{xy}\).

  \[J_{xy}=J_{12}= \int_V {\left ( \delta_{12} \, r^2 - x_1 x_2 \right) \rho} \mathrm{d}V = \int_V {\left ( -xy \right ) \rho} \mathrm{d}V = \] \[= - \rho \int_{- \frac {c}{2}}^{\frac {c}{2}} \int_{- \frac {b}{2}}^{\frac {b}{2}} \int_{- \frac {a}{2}}^{\frac {a}{2}} {xy} \, \mathrm{d}x \, \mathrm{d}y \, \mathrm{d}z = - \rho \int_{- \frac {c}{2}}^{\frac {c}{2}} \int_{- \frac {b}{2}}^{\frac {b}{2}} {\left [ \frac {x^2 y}{2} \right ]_{- \frac {a}{2}}^{\frac {a}{2}}} \, \mathrm{d}y \, \mathrm{d}z = - \rho \int_{- \frac {c}{2}}^{\frac {c}{2}} \int_{- \frac {b}{2}}^{\frac {b}{2}} {0} \, \mathrm{d}y \, \mathrm{d}z = 0 \]

  Zjistili jsme, že deviační moment \(J_{xy}\) je nulový. A co ostatní deviační momenty? Snadno ukážeme, že jsou také nulové – při jejich výpočtu dříve nebo později vždy narazíme na určitý integrál z nulové funkce. Proto platí rovnost:

  \[J_{xy} = J_{xz} = J_{yz} = 0 .\]

  Jelikož máme vypočítány všechny potřebné části tenzoru setrvačnosti homogenního kvádru, již nám jen zbývá zapsat je do matice:

  \[J= \begin{pmatrix} \frac {1}{12} m \left ( b^2 + c^2 \right ) & 0 & 0\\ 0 & \frac {1}{12} m \left ( a^2 + c^2 \right ) & 0\\ 0 & 0 & \frac {1}{12} m \left ( a^2 + b^2 \right ) \end{pmatrix} = \frac {1}{12} m \begin{pmatrix} b^2 + c^2 & 0 & 0\\ 0 & a^2 + c^2 & 0\\ 0 & 0 & a^2 + b^2 \end{pmatrix} .\]

• Komentář k Nápovědě 2

  Určeme \(J_{yy}\) i přímým výpočtem integrálu a ověřme, že dojdeme ke stejnému výsledku jako záměnou proměnných:

  \[J_{yy}=\int_V {\left ( x^2 + z^2 \right ) \rho} \mathrm{d}V = \rho \int_{- \frac {c}{2}}^{\frac {c}{2}} \int_{- \frac {b}{2}}^{\frac {b}{2}} \int_{- \frac {a}{2}}^{\frac {a}{2}} {\left ( x^2 + z^2 \right )} \mathrm{d}x \, \mathrm{d}y \, \mathrm{d}z .\]

  Využijme vlastnosti integrálu – integrovaná funkce je nezávislá na \(y\) – je tedy možné integrál podle \(y\) „vytknout“.

  \[J_{yy}= \rho \int_{- \frac {b}{2}}^{\frac {b}{2}} \mathrm{d}y \int_{- \frac {c}{2}}^{\frac {c}{2}} \int_{- \frac {a}{2}}^{\frac {a}{2}} {\left ( x^2 + z^2 \right )} \mathrm{d}x \, \mathrm{d}z = \rho \left [ y \right ]_{- \frac {b}{2}}^{\frac {b}{2}} \int_{- \frac {c}{2}}^{\frac {c}{2}} {\left [ \frac {x^3}{3} + xz^2 \right ]_{- \frac {a}{2}}^{\frac {a}{2}}} \mathrm{d}z=\] \[= ab \rho \int_{- \frac {c}{2}}^{\frac {c}{2}} {\left ( \frac {a^2}{12} + z^2 \right )} \mathrm{d}z = ab \rho \left [ \frac {z \, a^2}{12} + \frac {z^3}{3} \right ]_{- \frac {c}{2}}^{\frac {c}{2}} = abc \rho \frac {1}{12} \left ( a^2 + c^2 \right )\]

  Označíme-li tedy opět hmotnost tělesa \(m\), dostaneme vztah:

  \[J_{yy} = \frac {1}{12} m \left ( a^2 + c^2 \right ) .\]

• Nápověda 3

  Rozmyslete si, jaký vztah platí pro moment setrvačnosti vůči ose zadané směrovým vektorem a procházející daným bodem. Určete směrový vektor tělesové uhlopříčky kvádru.

• Řešení – Nápověda 3

  Pro moment setrvačnosti \(J_{\vec \nu}\) tyče vůči ose zadané jednotkovým vektorem \(\vec \nu\) platí:

  \[J_{\vec \nu} = J_{ij} \nu_i \nu_j .\]

  Odvození viz: Studijní text k teoretické mechanice tuhého tělesa.

  Je třeba si uvědomit, že v tomto vztahu jsou schovány dvě Einsteinovy sumační konvence, tedy:

  \[J_{\vec \nu} = \sum_{i=1}^{3} \, \sum_{j=1}^{3} \, J_{ij} \nu_i \nu_j .\]

  O něco přehlednější zápis je v maticové notaci:

  \[J_{\vec \nu} = \vec \nu \cdot J \cdot {\vec \nu}^T,\]

  kde \(J\) reprezentuje celou matici tenzoru setrvačnosti.

  Nejprve určeme směrový vektor \(\vec s\) tělesové uhlopříčky. Ten může být například \(\vec s = \left ( a, \, b, \, c \right )\). Určeme normu vektoru \(\vec s\):

  \[\left \| \vec s \right \| = \sqrt {a^2 + b^2 + c^2}.\]

  Ovšem tento vektor není jednotkový, budeme ho muset normovat. Náš jednotkový směrový vektor \(\vec \nu\) je tedy:

  \[\vec \nu = \frac {1}{\sqrt {a^2 + b^2 + c^2}} \left ( a, \, b, \, c \right ).\]

  Teď již zbývá jen užít znalostí lineární algebry a například pomocí maticové notace vypočítat hledaný moment setrvačnosti \(J_{\vec \nu}\).

  \[J_{\vec \nu} = \vec \nu \cdot J \cdot {\vec \nu}^T = \frac {1}{12} m \frac {1}{a^2 + b^2 + c^2}\,\begin{pmatrix} a, & b, & c \end{pmatrix} \begin{pmatrix} b^2 + c^2 & 0 & 0\\ 0 & a^2 + c^2 & 0\\ 0 & 0 & a^2 + b^2 \end{pmatrix} \begin{pmatrix} a\\ b\\ c \end{pmatrix}=\] \[= \frac {1}{12} m \frac {1}{a^2 + b^2 + c^2} \begin{pmatrix} a(b^2 + c^2), & b (a^2 + c^2), & c (a^2 + b^2) \end{pmatrix} \begin{pmatrix} a\\ b\\ c \end{pmatrix}=\] \[=\frac {m}{12(a^2 + b^2 + c^2)} \left [ a^2(b^2 + c^2) + b^2 (a^2 + c^2) + c^2 (a^2 + b^2) \right ] =\] \[=\frac {m(a^2 b^2 + a^2 c^2 + b^2 c^2)}{6(a^2 + b^2 + c^2)}\]

  Námi hledaný moment setrvačnosti kvádru vůči tělesové uhlopříčce je:

  \[J_{\vec \nu} = \frac {m(a^2 b^2 + a^2 c^2 + b^2 c^2)}{6(a^2 + b^2 + c^2)}.\]

• Celkové řešení

  Pro určení jednotlivých složek tenzoru setrvačnosti \(J_{jk}\) platí vztah:

  \[J_{jk}= \int_V {( \delta_{jk} \, r^2 - x_j \, x_k ) \rho} \, \mathrm{d}V,\tag{1}\]

  kde \(r\) je vzdálenost od počátku soustavy, \(\delta_{jk}\) je Kroneckerovo delta, \(\rho\) je hustota tělesa a souřadnice polohového vektoru \(x_i\) pro \(i=\) 1 až 3 jsou obecnějším zapsáním našich souřadnic \(x, \, y, \, z\).

  Určeme nejprve složku \(J_{xx}\) pomocí vztahu (1):

  \[J_{xx}=J_{11}= \int_V {\left ( \delta_{11} \, r^2 - x_1 x_1 \right) \rho} \mathrm{d}V = \int_V {\left ( x^2 + y^2 + z^2 - x^2 \right ) \rho} \mathrm{d}V =\int_V {\left ( y^2 + z^2 \right ) \rho} \mathrm{d}V.\]

  Tento objemový integrál budeme počítat jako integrál proměnných \(x, \, y\) a \(z\). Jelikož je střed naší soustavy v těžišti kvádru, budeme integrovat od \(- \frac {d}{2}\) po \(\frac {d}{2}\), kde \(d\) je délka příslušné hrany. Také využijeme toho, že hustota \(\rho\) je konstantní a vytkneme ji před integrál.

  \[J_{xx}= \rho \int_{- \frac {c}{2}}^{\frac {c}{2}} \int_{- \frac {b}{2}}^{\frac {b}{2}} \int_{- \frac {a}{2}}^{\frac {a}{2}} {\left ( y^2 + z^2 \right )} \mathrm{d}x \, \mathrm{d}y \, \mathrm{d}z = \rho \int_{- \frac {c}{2}}^{\frac {c}{2}} \int_{- \frac {b}{2}}^{\frac {b}{2}} {\left ( y^2 + z^2 \right ) \left [ x \right ]_{- \frac {a}{2}}^{\frac {a}{2}}} \mathrm{d}y \, \mathrm{d}z =\] \[= a \rho \int_{- \frac {c}{2}}^{\frac {c}{2}} \int_{- \frac {b}{2}}^{\frac {b}{2}} {\left ( y^2 + z^2 \right )} \mathrm{d}y \, \mathrm{d}z = a \rho \int_{- \frac {c}{2}}^{\frac {c}{2}} {\left [ \frac {y^3}{3} + y \, z^2 \right]_{- \frac {b}{2}}^{\frac {b}{2}}} \mathrm{d}z = a \rho \int_{- \frac {c}{2}}^{\frac {c}{2}} {\left ( \frac {2 \, b^3}{24} + b \, z^2 \right)} \mathrm{d}z =\] \[= ab \rho \int_{- \frac {c}{2}}^{\frac {c}{2}} {\left ( \frac {b^2}{12} + z^2 \right)} \mathrm{d}z = ab \rho \left [ \frac {z \, b^2}{12} + \frac {z^3}{3} \right ]_{- \frac {c}{2}}^{\frac {c}{2}} = ab \rho \frac {1}{3} \left [ \frac {z \, b^2}{4} + z^3 \right ]_{- \frac {c}{2}}^{\frac {c}{2}} = ab \rho \frac {1}{3} \left ( \frac {c \, b^2}{4} + \frac {c^3}{4} \right ) = \] \[= \frac {1}{12} abc \rho \left ( b^2 + c^2 \right )\]

  Výraz \(abc \rho\) odpovídá celkové hmotnosti našeho kvádru, označme ji \(m\) a poté můžeme první složku tenzoru setrvačnosti zapsat jako:

  \[J_{xx} = \frac {1}{12} m \left ( b^2 + c^2 \right ) .\]

  Cyklickou záměnou rozměrů kvádru ve směrech os \(x\), \(y\) a \(z\) určíme složky \(J_{yy}\) a \(J_{zz}\).

  \[J_{yy} = \frac {1}{12} m \left ( a^2 + c^2 \right )\] \[J_{zz} = \frac {1}{12} m \left ( a^2 + b^2 \right )\]

  Příroda nerozlišuje osy \(x\), \(y\) a \(z\), a proto musí být vztahy stejné, jen s příslušnými rozměry. (Ověření viz Tenzor setrvačnosti kvádru, Komentář k Nápovědě 2.)

  Tím jsme vyřešili složky tenzoru, které představují jednotlivé momenty setrvačnosti vůči osám soustavy. Na řadě jsou deviační momenty a stačí si uvědomit, že „hmota“ kvádru je symetricky rozložena vzhledem k osám souřadnic, a proto musí být deviační momenty nulové.

  (Ověření viz Tenzor setrvačnosti kvádru, Řešení – Nápověda 2.)

  Nyní jen zapíšeme všechny potřebné části tenzoru setrvačnosti homogenního kvádru do matice:

  \[J= \begin{pmatrix} \frac {1}{12} m \left ( b^2 + c^2 \right ) & 0 & 0\\ 0 & \frac {1}{12} m \left ( a^2 + c^2 \right ) & 0\\ 0 & 0 & \frac {1}{12} m \left ( a^2 + b^2 \right ) \end{pmatrix} = \frac {1}{12} m \begin{pmatrix} b^2 + c^2 & 0 & 0\\ 0 & a^2 + c^2 & 0\\ 0 & 0 & a^2 + b^2 \end{pmatrix} .\]

  Pro moment setrvačnosti \(J_{\vec \nu}\) tyče vůči ose zadané jednotkovým vektorem \(\vec \nu\) platí:

  \[J_{\vec \nu} = J_{ij} \nu_i \nu_j .\tag{2}\]

  O něco přehledněji lze vztah (2) zapsat maticově:

  \[J_{\vec \nu} = \vec \nu \cdot J \cdot {\vec \nu}^T,\]

  kde \(J\) reprezentuje celou matici tenzoru setrvačnosti.

  Vyberme si směrový vektor \(\vec s\) tělesové uhlopříčky. Ten může být například \(\vec s = \left ( a, \, b, \, c \right )\). Určeme normu vektoru \(\vec s\):

  \[\left \| \vec s \right \| = \sqrt {a^2 + b^2 + c^2} .\]

  Vidíme, že \(\left \| \vec s \right \| \neq 1 \), budeme ho muset normovat. Jednotkový směrový vektor tělesové uhlopříčky \(\vec \nu\) je tedy:

  \[\vec \nu = \frac {1}{\sqrt {a^2 + b^2 + c^2}} \left ( a, \, b, \, c \right ).\]

  Nyní pomocí maticové notace (2) vypočítáme hledaný moment setrvačnosti \(J_{\vec \nu}\).

  \[J_{\vec \nu} = \vec \nu \cdot J \cdot {\vec \nu}^T = \frac {1}{12} m \frac {1}{a^2 + b^2 + c^2}\,\begin{pmatrix} a, & b, & c \end{pmatrix} \begin{pmatrix} b^2 + c^2 & 0 & 0\\ 0 & a^2 + c^2 & 0\\ 0 & 0 & a^2 + b^2 \end{pmatrix} \begin{pmatrix} a\\ b\\ c \end{pmatrix}=\] \[= \frac {1}{12} m \frac {1}{a^2 + b^2 + c^2} \begin{pmatrix} a(b^2 + c^2), & b (a^2 + c^2), & c (a^2 + b^2) \end{pmatrix} \begin{pmatrix} a\\ b\\ c \end{pmatrix}=\] \[=\frac {m}{12(a^2 + b^2 + c^2)} \left [ a^2(b^2 + c^2) + b^2 (a^2 + c^2) + c^2 (a^2 + b^2) \right ] =\] \[=\frac {m(a^2 b^2 + a^2 c^2 + b^2 c^2)}{6(a^2 + b^2 + c^2)}\]

  Námi hledaný moment setrvačnosti kvádru vůči tělesové uhlopříčce je:

  \[J_{\vec \nu} = \frac {m(a^2 b^2 + a^2 c^2 + b^2 c^2)}{6(a^2 + b^2 + c^2)}.\]

• Odpověď

  Tenzor setrvačnosti homogenního kvádru vůči jeho těžišti je:

  \[J = \frac {1}{12} m \begin{pmatrix} b^2 + c^2 & 0 & 0\\ 0 & a^2 + c^2 & 0\\ 0 & 0 & a^2 + b^2 \end{pmatrix} .\]

  Námi hledaný moment setrvačnosti vůči tělesové uhlopříčce je:

  \[J_{\vec \nu} = \frac {m(a^2 b^2 + a^2 c^2 + b^2 c^2)}{6(a^2 + b^2 + c^2)} .\]

• Komentář – tenzor setrvačnosti krychle

  Pro krychli platí, že \(a=b=c\), tedy pro tenzor setrvačnosti krychle \(J_k\) vzhledem k jejímu hmotnému středu bude platit:

  \[J_k= \frac {1}{12} m \begin{pmatrix} 2 a^2 & 0 & 0\\ 0 & 2 a^2 & 0\\ 0 & 0 & 2 a^2 \end{pmatrix}= \frac {{ma}^2}{6} \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix}= \frac {{ma}^2}{6} \mathbb{E} , \]

  kde \(\mathbb{E}\) je jednotková matice.

  Určeme moment setrvačnosti krychle vůči libovolné ose procházející těžištěm krychle, která je určena obecným jednotkovým vektorem \(\vec n\).

  \[J_\vec n = \vec n \, J_k \, {\vec n}^T = \vec n \, \left ( \frac {{ma}^2}{6} \mathbb{E} \, \right ) {\vec n}^T = \frac {{ma}^2}{6} \vec n \, \mathbb{E} \, {\vec n}^T = \frac {{ma}^2}{6} \vec n \, {\vec n}^T = \frac {{ma}^2}{6} \| \vec n \| = \frac {{ma}^2}{6} \]

  Tedy moment setrvačnosti krychle vůči libovolné ose procházející jejím těžištěm je \(\frac {{ma}^2}{6}\).

  Jinak řečeno, krychle je tak krásně symetrické těleso, že ať jejím středem proložíme osu otáčení jakkoliv, rozložení hmoty okolo této osy bude mít při rotaci stejný efekt. Tato vlastnost se objevuje i u koule. Viz Komentář – tenzor setrvačnosti koule.