Sbírka řešených úloh

Hmotný bod na kouli

Úloha číslo: 948

• Nápověda 1

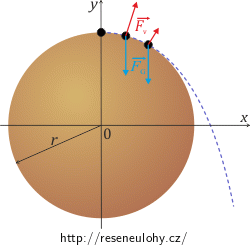
  Nejprve si nakreslete obrázek, rozmyslete si, jaké síly působí na hmotný bod a jaké jsou podmínky odtrhnutí hmotného bodu od koule.

• Řešení nápovědy 1

  

  Hmotný bod se odtrhne od koule v okamžiku, kdy bude vazbová síla \(\vec{F_v}\) rovna nule.

  Tíhovou sílu \(\vec{F_G}\) můžeme vyjádřit jako:

  \[\vec{F_G}=(0,-mg).\]

• Nápověda 2

  Napište Lagrangeovy rovnice I. druhu a podmínku vazby pro pohyb hmotného bodu před „odtržením od koule“.

• Komentář

  Úloha je sice zadaná v trojrozměrném prostoru, ale všimněte si, že jí můžeme snadno převést na dvoudimensionální úlohu, pokud si vybereme rovinu, ve které se pohyb hmotného bodu děje.

• Řešení nápovědy 2

  Lagrangeovy rovnice I. druhu zní:

  \[m\ddot{x} =\lambda\frac{\partial{G}}{\partial{x}},\tag{1}\] \[m\ddot{y}=-mg+\lambda\frac{\partial{G}}{\partial{y}}\tag{2}\]

  a rovnice vazby:

  \[ G=x^2+y^2-r^2=0 . \tag{3}\]

  Diferencováním rovnice (3) podle jednotlivých proměnných získáme následující vztahy:

  \[ \frac{\partial{G}}{\partial{x}}=2x ,\] \[\frac{\partial G}{\partial y}=2y .\]

  Po dosazení do (1) a (2) dostáváme:

  \[m\ddot{x}=2\lambda x,\] \[m\ddot{y}=-mg+2\lambda y . \]

  Rovnice ještě vydělíme hmotností m:

  \[ \ddot{x}=\frac{2\lambda x}{m},\tag{4}\] \[ \ddot{y}=-g+\frac{2\lambda y}{m}.\tag{5}\]

  V rovnicích zbývá neznámá λ. Nachází se ve členech, které představují vazbovou sílu. Vazbová síla se v průběhu pohybu mění. Napišme si její vyjádření:

  \[\vec{F_v}=\left(\lambda\frac{\partial{G}}{\partial{x}},\lambda\frac{\partial{G}}{\partial{y}}\right)=(2x\lambda,2y\lambda).\]

• Nápověda 3

  V Lagrangeových rovnicích (4) a (5) sestavených v minulé nápovědě zůstává λ, která vystupuje ve ztahu pro vazbovou sílu. Vhodným postupem, jak ji vyjádřit, je derivovat rovnici (3) dvakrát podle času.

• Řešení nápovědy 3

  Derivujeme-li rovnici (3) dvakrát podle času, získáme rovnici:

  \[\dot{G}=\frac{\mathrm{d}G}{\mathrm{d}t}=2x\dot{x}+2y\dot{y}, \] \[ \ddot{G}=\dot{x}^2+x\ddot{x}+\dot{y}^2+y\ddot{y}=0. \]

  Dosazením za \(\ddot{x}\) a \(\ddot{y}\) společně s použitím vztahu pro kvadrát rychlosti v získáme:

  \[ v^2+\frac{2\lambda x^2}{m}+\frac{2\lambda y^2}{m} - gy=0. \]

  Prostřední dva členy lze díky vazbové podmínce upravit na \(\frac{2\lambda r^2}{m}\) a získáme vztah:

  \[v^2+\frac{2\lambda r^2}{m}-gy=0.\]

  Nyní vyjádříme λ:

  \[ \lambda=\frac{(gy-v^2)m}{2r^2}. \]

• Nápověda 4

  V předchozí nápovědě jsme odvodili vztah pro λ. Vazbová síla, a tím i koeficient λ nabývají v okamžiku odtrhnutí hmotného bodu nulové hodnoty. Položte tedy λ = 0 a s využitím zákona zachování mechanické energie vyjádřete souřadnici y ve chvíli odtržení hmotného bodu od koule.

• Řešení nápovědy 4

  Položíme λ rovno nule:

  \[ \lambda=\frac{(gy-v^2)m}{2r^2}=0.\]

  Výraz je nulový právě tehdy, když je závorka v čitateli rovna nule. Získáváme tedy podmínku:

  \[gy-v^2=0.\tag{6}\]

  V tuto chvíli je vhodné podívat se, co nám pro hmotný bod říká zákon zachování mechanické energie

  \[ E=E_{k}+E_{p}=\frac{1}{2}mv^2+mgy.\tag{7}\]

  Z počáteční podmínky (rychlost je nulová, a tedy i kinetická energie je nulová) určíme hodnotu celkové mechanické energie jako:

  \[E=mgr.\]

  Celkovou energii a vyjádření \(v^2=yg\) plynoucí z podmínky (6) využijeme k napsání rovnice:

  \[mgr=mgy+\frac{1}{2}mgy.\]

  Po úpravě získáváme hledané řešení:

  \[y=\frac{2}{3}r.\]

• Celkové řešení

  Napíšeme Lagrangeovy rovnice I. druhu a vazbovou podmínku pro hmotný bod pohybující se po kouli.

  \[m\ddot{x} =\lambda\frac{\partial{G}}{\partial{x}},\tag{1}\] \[m\ddot{y}=-mg+\lambda\frac{\partial{G}}{\partial{y}},\tag{2}\] \[ G=x^2+y^2-r^2=0.\tag{3}\]

  Do rovnic (1) a (2) můžeme dosadit za parciální derivace vazbové podmínky (3) (viz nápověda 2). Po úpravě tak získáme vyjádření:

  \[ \ddot{x}=\frac{2\lambda x}{m},\tag{4}\] \[ \ddot{y}=-g+\frac{2\lambda y}{m}. \tag{5}\]

  V rovnicích zbývá neznámá λ. Nachází se ve členech, které představují vazbovou sílu. Vazbová síla se v průběhu pohybu mění. Napišme si její vyjádření:

  \[\vec{F_v}=\left(\lambda\frac{\partial{G}}{\partial{x}},\lambda\frac{\partial{G}}{\partial{y}}\right)=(2x\lambda,2y\lambda).\]

  Abychom zjistili, jak se vazbová síla mění, musíme vyjádřit λ. (Návod naleznete v nápovědě 3). Pro λ platí:

  \[ \lambda=\frac{(gy-v^2)m}{2r^2}. \]

  Jelikož vazbová síla v okamžiku odtrhnutí hmotného bodu od koule je nulová, musí být i koeficient λ nulový:

  \[ \lambda=\frac{(gy-v^2)m}{2r^2}=0.\]

  Výraz je nulový právě tehdy, když je závorka v čitateli rovna nule. Získáváme tedy podmínku:

  \[gy-v^2=0.\tag{6}\]

  V tuto chvíli je vhodné podívat se, co nám pro hmotný bod říká zákon zachování mechanické energie

  \[ E=E_{k}+E_{p}=\frac{1}{2}mv^2+mgy.\tag{7}\]

  Z počáteční podmínky (rychlost je nulová, a tedy i kinetická energie je nulová) určíme hodnotu celkové mechanické energie jako:

  \[E=mgr.\]

  Celkovou energii a vyjádření \(v^2=yg\) plynoucí z podmínky (6) dosadíme do rovnice (7), a získáváme tak vyjádření:

  \[mgr=mgy+\frac{1}{2}mgy.\]

  Po úpravě získáváme hledané řešení.

  \[y=\frac{2}{3}r.\]

  Tento výsledek je již hledaným řešením, protože nám určuje místo odtrhnutí hmotného bodu od koule.

• Odpověď

  Hmotný bod se odpojí od koule ve výšce:

  \[y=\frac{2}{3}r.\]

• Poznámka

  Při řešení úlohy jsme předpokládali, že ve chvíli, kdy se hmotný bod nachází na vrcholu koule, je jeho počáteční rychlost v₀ nulová. Pokusme se ještě odvodit vztah pro oddělení hmotného bodu od koule za předpokladu nenulové počáteční rychlosti v₀.

  Celková mechanická energie hmotného bodu tak bude mít hodnotu:

  \[E=E_k+E_p=\frac{1}{2}mv_0^2+mgr.\]

  Využitím vztahu (6) z nápovědy 4, který plyne z nulovosti vazbové síly v okamžiku odtržení ve tvaru:

  \[y=\frac{v^2}{g}.\]

  Dosadíme za y z předchozího vztahu a za celkovou mechanickou energii E do rovnice (7):

  \[\frac{1}{2}mv_0^2+mgr=mgy+\frac{1}{2}mgy.\]

  Vyjádříme-li z rovnice y, získáváme výšku y, ve které opustí hmotný bod kouli:

  \[y=\frac{2}{3}r+\frac{v_0^2}{3g}.\]

• Odkaz

  Úlohu je možné řešit i bez Lagrangeových rovnic, jen pomocí klasické mechaniky. Toto řešení naleznete v úloze:

  Skluz tělesa po povrchu koule.