Sbírka řešených úloh

Dvojzvratná páka

Úloha číslo: 1140

Ve svislé rovině zvolme systém souřadnic x, y, jehož kladná osa y nechť míří svisle dolů. V této rovině uvažujeme lomenou dvojzvratnou páku AOB, otáčivou kolem pevného bodu O = [0, 0], v jejichž koncových bodech A = [x₁, y₁], B = [x₂, y₂] působí tíhy \(\vec{F}_1\) a \(\vec{F}_2\) (viz obrázek).Určete rovnovážné polohy páky, nepřihlížíme-li k její hmotnosti a ani ke tření.

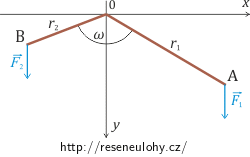
• Nápověda 1

  Ramena dvojzvratné páky svírají stálý úhel ω. Rovnovážná poloha bude určena, pokud budeme znát souřadnice bodů A a B. K tomu postačí jediný parametr, úloha má jediný stupeň volnosti, a to např. úhel φ, který je pro další výpočet výhodné měřit od osy y (viz obrázek).

  Napište závislost souřadnic bodů A a B na úhlu φ.

  

• Goniometrické vzorce

  Pro vyjádření souřadnic bodů A a B se nám budou hodit součtové vzorce pro goniometrické funkce.

  Pro každá dvě reálná čísla x, y platí:

  \[\sin{(x+y)}=\sin{x}\cos{y}+\cos{x}\sin{y},\] \[\sin{(x-y)}=\sin{x}\cos{y}-\cos{x}\sin{y},\] \[\cos{(x+y)}=\cos{x}\cos{y}-\sin{x}\sin{y},\] \[\cos{(x-y)}=\cos{x}\cos{y}+\sin{x}\sin{y}.\]

• Řešení nápovědy 1

  Souřadnice bodů A a B mají následující vyjádření:

  \[x_1=r_1\sin{\varphi}\] \[y_1=r_1\cos{\varphi}\] \[x_2=-r_2\sin{(\omega -\varphi)}=-r_2\sin{\omega}\cos{\varphi}+r_2\cos{\omega}\sin{\varphi}\] \[y_2=r_2\cos{(\omega -\varphi)}=r_2\cos{\omega}\cos{\varphi}+r_2\sin{\omega}\sin{\varphi}.\]

  V úpravách vyjádření souřadnic bodu B jsme použili součtové vzorce pro goniometrické funkce (viz přechozí oddíl – goniometrické vzorce).

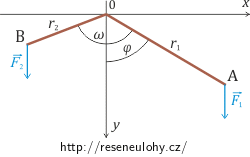
• Nápověda 2

  Rovnovážnou polohu dvojzvratné páky hledáme pomocí zobecněného principu virtuální práce. K tomu je zapotřebí hledat tzv. vratná virtuální posunutí slučitelná s vazbami. Napište je nejprve obecně pro každou souřadnici a poté dosaďte konkrétní vyjádření jednotlivých souřadnic.

• Řešení nápovědy 2 – obecný tvar

  Virtuální posunutí v jednotlivých souřadnicích jsme se rozhodli vyjádřit pomocí infinitezimální změny úhlu \(\varphi\). Obecné rovnice pro každé posunutí proto mají tvar:

  \[\delta x_1=\frac{\mathrm{d}x_1}{\mathrm{d}\varphi}\delta\varphi ,\] \[\delta y_1=\frac{\mathrm{d}y_1}{\mathrm{d}\varphi}\delta\varphi ,\] \[\delta x_2=\frac{\mathrm{d}x_2}{\mathrm{d}\varphi}\delta\varphi ,\] \[\delta y_2=\frac{\mathrm{d}y_2}{\mathrm{d}\varphi}\delta\varphi .\]

• Řešení nápovědy 2 – dosazení

  Dosazujeme do obecného tvaru vypočtené derivace souřadnic podle úhlu \(\varphi\):

  \[\delta x_1=r_1\cos{\varphi}\delta\varphi,\] \[\delta y_1=-r_1\sin{\varphi}\delta\varphi,\] \[\delta x_2=(r_2\sin{\omega}\sin{\varphi}+r_2\cos{\omega}\cos{\varphi})\delta\varphi,\] \[\delta y_2=(-r_2\cos{\omega}\sin{\varphi}+r_2\sin{\omega}\cos{\varphi})\delta\varphi.\]

• Nápověda 3

  Zobecněný princip virtuální práce tvrdí, že práce vtištěných sil při libovolných virtuálních posunutích slučitelných s vazbami je nulová. Abychom tedy mohli zobecněný princip virtuální práce použít, musíme znát vtištěné síly, které na zkoumaný objekt působí. Na dvojzvratnou páku působí pouze dvě vtištěné síly (viz zadání). Rozepište tyto síly po složkách a dosaďte do zobecněného principu virtuální práce.

• Řešení nápovědy 3 – síly po složkách

  V zadání je řečeno, že na dvojzvratnou páku působí dvě síly. Je to síla \(\vec{F}_1\) v bodě A a síla \(\vec{F}_2\) v bodě B. Vzhledem k zavedení souřadnic mají složky obou sil následující tvar:

  \[\vec{F}_1=(0,F_1),\] \[\vec{F}_2=(0,F_2).\]

• Řešení nápovědy 3 – zobecněný princip virtuální práce

  Zobecněný princip virtuální práce má tvar:

  \[\sum_{i=1}^N \vec{F_i}\cdot\delta\vec{r_i}=0,\]

  kde \(\vec{F_i}\) jsou výslednice vtištěných sil na i-tý hmotný bod a \(\vec{r_i}\) jsou virtuální posunutí slučitelná s vazbami i-tého hmotného bodu.

  Vzhledem k tomu, že v x-ové souřadnici jsou složky obou sil nulové, nemusíme uvažovat členy, obsahující tyto složky. Proto bude zobecněný princip virtuální práce vypadat v našem případě takto:

  \[F_1\delta y_1+F_2\delta y_2=0.\]

  Tedy po dosazení:

  \[F_1\delta y_1+F_2\delta y_2=-F_1r_1\sin{\varphi}\delta\varphi-F_2r_2\cos{\omega}\sin{\varphi}\delta\varphi+F_2r_2\sin{\omega}\cos{\varphi}\delta\varphi=0.\]

  Ve všech členech poslední rovnosti vystupuje \(\delta\varphi\). Jelikož tato rovnost má platit pro libovolná virtuální posunutí \(\delta\varphi\), můžeme rovnici \(\delta\varphi\) vydělit.

  Získáme tak podmínku:

  \[-F_1r_1\sin{\varphi}-F_2r_2\cos{\omega}\sin{\varphi}+F_2r_2\sin{\omega}\cos{\varphi}=0.\]

  Z tohoto vztahu bychom rádi vyjádřili úhel \(\varphi\), což je hledaná podmínka rovnováhy dvojzvratné páky.

  Vytknutím goniometrických funkcí a převedením získáváme vztah:

  \[\sin{\varphi}(F_1r_1+F_2r_2\cos{\omega})=\cos{\varphi}F_2r_2\sin{\omega}.\]

  S použitím vzorce \(\mathrm{tg}\,\varphi=\frac{\sin{\varphi}}{\cos{\varphi}}\) dospíváme k:

  \[\mathrm{tg}\,\varphi=\frac{F_2r_2\sin{\omega}}{F_1r_1+F_2r_2\cos{\omega}}.\]

  Rovnice pro φ má na intervalu (-π/2, 3π/2) dvě řešení, která jsou od sebe vzdálena o úhel π. Řešení v intervalu (-π/2, π/2) odpovídá stabilní poloze a řešení v intervalu (π/2, 3π/2) odpovídá labilní poloze. V případě labilní polohy páka „balancuje“ na špičce v ose otáčení.

• Celkové řešení

  Pro zobecněný princip virtuální práce je třeba znát virtuální posunutí slučitelná s vazbami jednotlivých souřadnic a působící vtištěné síly.

  Vyjádření souřadnic je vhodné provést pomocí úhlu φ, který určuje odklon ramena délky r₁ od svislého směru (viz nápověda 1). Souřadnice bodů A a B mají následující vyjádření:

  \[x_1=r_1\cos{\varphi},\] \[y_1=r_1\sin{\varphi},\] \[x_2=-r_2\cos{(\omega -\varphi)}=-r_2\cos{\omega}\cos{\varphi}-r_2\sin{\omega}\sin{\varphi},\] \[y_2=r_2\sin{(\omega -\varphi)}=r_2\sin{\omega}\cos{\varphi}-r_2\cos{\omega}\sin{\varphi}.\]

  Virtuální posunutí pro jednotlivé souřadnice obou bodů v závislosti na úhlu \(\varphi\) mají tvar:

  \[\delta x_1=\frac{\mathrm{d}x_1}{\mathrm{d}\varphi}\delta\varphi=-r_1\sin{\varphi}\delta\varphi,\] \[\delta y_1=\frac{\mathrm{d}x_1}{\mathrm{d}\varphi}\delta\varphi=r_1\cos{\varphi}\delta\varphi,\] \[\delta x_2=\frac{\mathrm{d}x_1}{\mathrm{d}\varphi}\delta\varphi=(r_2\cos{\omega}\sin{\varphi}-r_2\sin{\omega}\cos{\varphi})\delta\varphi,\] \[\delta y_2=\frac{\mathrm{d}x_1}{\mathrm{d}\varphi}\delta\varphi=(-r_2\sin{\omega}\sin{\varphi}-r_2\cos{\omega}\cos{\varphi})\delta\varphi.\]

  Síly mají vzhledem k zavedení souřadnic složky:

  \[\vec{F}_1=(0,F_1),\] \[\vec{F}_2=(0,F_2).\]

  Zobecněný princip virtuální práce zní:

  \[\sum_{i=1}^N \vec{F_i}\cdot\delta\vec{r_i}=0,\]

  kde \(\vec{F_i}\) jsou výslednice vtištěných sil na i-tý hmotný bod a \(\vec{r_i}\) jsou virtuální posunutí slučitelná s vazbami i-tého hmotného bodu.

  Všechny potřebné veličiny již známe, proto můžeme dosadit:

  \[F_1\delta y_1+F_2\delta y_2=F_1r_1\sin{\varphi}\delta\varphi-F_2r_2\cos{\omega}\sin{\varphi}\delta\varphi+F_2r_2\sin{\omega}\cos{\varphi}\delta\varphi=0.\]

  Vyjádříme úhel φ (viz nápověda 3), což je hledaná podmínka rovnováhy:

  \[\mathrm{tg}\,\varphi=\frac{F_2r_2\sin{\omega}}{F_1r_1+F_2r_2\cos{\omega}}.\]

  Rovnice má pro φ na intervalu (-π/2, 3π/2) dvě řešení, která jsou od sebe vzdálena o úhel π. Řešení v intervalu (-π/2, π/2) odpovídá stabilní poloze a řešení v intervalu (π/2, 3π/2) odpovídá labilní poloze. V případě labilní polohy páka „balancuje“ na špičce v ose otáčení.

• Odpověď

  Rovnováha dvojzvratné páky nastane při úhlu φ:

  \[\mathrm{tg}\varphi=\frac{F_2r_2\sin{\omega}}{F_1r_1+F_2r_2\cos{\omega}}.\]

  Rovnice má pro úhel φ dvě řešení. Jedno stabilní a druhé labilní. Tato řešení jsou od sebe vzálena o úhel π.