Tenzor setrvačnosti tenkého disku
Úloha číslo: 2249
Určete tenzor setrvačnosti velmi tenkého homogenního disku o poloměru \(R\) a hmotnosti \(M\) vzhledem k jeho hmotnému středu.
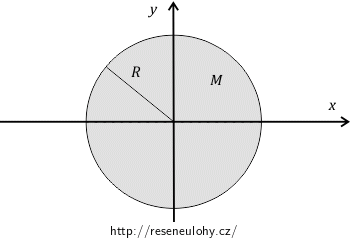
Disk je umístěn v 3D prostoru, osa \(z\) míří ven z nákresny a prochází středem disku.
Nápověda 1
Rozvažte, jakých vztahů budete užívat a jaké všechny veličiny budete potřebovat k výpočtu tenzoru setrvačnosti.
Dále si rozmyslete, v jakých souřadnicích bude výhodné pracovat, jaké platí transformační vztahy a jaký je význam determinantu Jacobiho matice (jakobiánu). Určete jakobián.
Nápověda 2
Vypočítejte postupně jednotlivé složky tenzoru setrvačnosti a zapište je do matice.
Celkové řešení
Pro určení jednotlivých složek tenzoru setrvačnosti \(J_{jk}\) spojitého tělesa bude platit vztah:
\[J_{jk}= \int_V^{}{( \delta_{jk} \, r^2 - x_j \, x_k ) \rho} \, \mathrm{d}V,\]kde \(r\) je vzdálenost „kousků“ disku od počátku soustavy, \(\delta_{jk}\) je Kroneckerovo delta a souřadnice polohového vektoru \(x_i\) pro \(i=\) 1 až 3 jsou obecnějším zapsáním našich souřadnic \(x, \, y, \, z\).
Je nutné znát i hustotu tělesa \(\rho\). Náš disk je velmi tenký, proto hutotu \(\rho\) nahradíme plošnou hustotou \(\sigma\) a budeme tudíž pracovat s plošným integrálem.
\[J_{jk}= \int_S^{}{( \delta_{jk} \, r^2 - x_j \, x_k ) \sigma} \, \mathrm{d}x\mathrm{d}y\]Hustota \(\sigma\) je konstantní, jelikož je disk homogenní.
Náš disk lze parametrizovat jako kruh o poloměru \(R\) ležící v rovině \(xy\). Jelikož počátek naší soustavy souřadnic splývá se středem disku, je \(z=0\) a
\[x = r \cos \varphi \, ,\] \[y = r \sin \varphi \, ,\]kde \(r\) je vzdálenost od počátku soustavy, probíhající interval \( \left\langle 0,R \right\rangle \). Úhel \(\varphi\) je měřený od osy \(x\) v rovině \(xy\) proti směru hodinových ručiček a \(\varphi \in \left( 0, 2 \pi \right\rangle \).
Pracujeme s plošným integrálem v polárních souřadnicích a pro výpočet dvojného integrálu v polárních souřadnicích bude nutné spočítat jakobián.
Jakobián \(\left| \mathbb{J} \right|\) (absolutní hodnota determinantu Jacobiho matice \(\mathbb{J}\)) udává vztah, jakým se při transformaci souřadnic mění objem diferenciálního útvaru.
Poznámka: hezký materiál pojednávající o významu Jacobiánu (anglicky): Lecture 5: Jacobians.Význam jakobiánu při počítání dvojného integrálu by se dal pro přechod z kartézských do polárních souřadnic vyjádřit vztahem:
\[\int_S f(x,y) \,\mathrm{d}x \,\mathrm{d}y = \int_S f(r,\varphi) \left| \mathbb{J} \right| \mathrm{d}r \,\mathrm{d}\varphi .\]Nyní spočítáme jakobián \(\left| \mathbb{J} \right|\).
\[\left| \mathbb{J} \right| = \begin{vmatrix} \frac{\mathrm{d}x}{\mathrm{d}r} & \frac{\mathrm{d}x}{\mathrm{d}\varphi} \\ \frac{\mathrm{d}y}{\mathrm{d}r} & \frac{\mathrm{d}y}{\mathrm{d}\varphi} \end{vmatrix} = \begin{vmatrix} \cos\varphi & - r \,\sin\varphi \\ \sin\varphi & r \,\cos\varphi \end{vmatrix} = r \cos^2 \varphi + r \sin^2 \varphi = r \]Určeme nejprve složku \(J_{zz}\) hledaného momentu setrvačnosti:
\[J_{zz}=J_{33}= \int_S {\left ( \delta_{33} \, r^2 - x_3 x_3 \right) \,\sigma} \mathrm{d}x \mathrm{d}y = \int_S {\left ( x^2 + y^2 + z^2 - z^2 \right ) \,\sigma} \mathrm{d}x \mathrm{d}y =\int_S {\left ( x^2 + y^2 \right ) \,\sigma} \mathrm{d}x \mathrm{d}y.\]Nyní přejdeme do polárních souřadnic a dosadíme za \(x\) a \(y\).
\[J_{zz} = \int_0^{2\pi} \int_0^R {\left[ \left( r \cos\varphi \right)^2 + \left( r \sin\varphi \right)^2 \right] \,\sigma \, r} \mathrm{d}r \mathrm{d}\varphi = \sigma \int_0^{2\pi} \int_0^R {\left(\cos^2\varphi + \sin^2\varphi \right) \, r^3 } \mathrm{d}r \mathrm{d}\varphi= \] \[=\sigma \int_0^{2\pi} 1 \mathrm{d}\varphi \int_0^R r^3 \mathrm{d}r=\sigma \left[ \varphi \right]_0^{2\pi} \left[ \frac {r^4}{4} \right]_0^R = \frac {2 \,\pi \,\sigma R^4}{4} = \frac { R^2}{2} \,\sigma \,\pi \, R^2\]Vztah \(\,\sigma \,\pi \, R^2\) je plošná hustota násobená plochou disku – což je hmotnost disku \(M\). Pak pro složku \(J_{zz}\) dostaneme vztah:
\[J_{zz}=\frac {M \, R^2}{2} .\]Rozložení hmotnosti disku vzhledem k osám \(x\) a \(y\) je totožné, z čehož plyne, že i moment setrvačnosti disku vzhledem k těmto dvěma osám bude stejný, a proto \(J_{xx}=J_{yy}\). Určeme \(J_{xx}\).
\[J_{xx}=J_{11}= \int_S {\left ( \delta_{11} \, r^2 - x_1 x_1 \right) \,\sigma} \mathrm{d}x \mathrm{d}y =\int_S {\left ( y^2 + z^2 \right ) \,\sigma} \mathrm{d}x \mathrm{d}y\] \[J_{xx} = \int_0^{2\pi} \int_0^R \left( r \sin\varphi \right)^2 r \,\sigma \mathrm{d}r \mathrm{d} \varphi = \sigma \int_0^{2\pi} \sin^2\varphi \mathrm{d} \varphi \int_0^R r^3 \mathrm{d}r\] \[\int_0^{2 \pi} \sin^2 \varphi \,\mathrm{d}\varphi = \int_0^{2 \pi} \frac {1 - \cos 2 \varphi}{2} \,\mathrm{d}\varphi = \left [ \frac {\varphi}{2} - \frac {\sin 2 \varphi}{4} \right ]_0^{2 \pi}= \pi\] \[J_{xx} = \sigma \pi \left[ \frac {R^4}{4} \right]_0^R = \frac {\pi \,\sigma R^4}{4} = \frac {M R^2}{4} = J_{yy}\]Teď se podívejme na deviační momenty.
\[J_{xz}=J_{13}= \int_S {\left ( \delta_{13} \, r^2 - x_1 x_3 \right) \,\sigma} \mathrm{d}x \mathrm{d}y = - \int_S {xz \,\sigma} \mathrm{d}x \mathrm{d}y =\int_0^{2\pi} \int_0^R 0 \,\mathrm{d}r \mathrm{d} \varphi = 0\] \[J_{yz}=J_{23}= \int_S {\left ( \delta_{23} \, r^2 - x_2 x_3 \right) \,\sigma} \mathrm{d}x \mathrm{d}y = - \int_S { yz \,\sigma} \mathrm{d}x \mathrm{d}y =\int_0^{2\pi} \int_0^R 0 \,\mathrm{d}r \mathrm{d} \varphi = 0\] \[J_{xy}=J_{12}= \int_S {\left ( \delta_{12} \, r^2 - x_1 x_2 \right) \,\sigma} \mathrm{d}x \mathrm{d}y = - \int_S {xy \,\sigma} \mathrm{d}x \mathrm{d}y =\sigma \int_0^{2\pi} \int_0^R r^2 \sin\varphi \cos \varphi \, r \,\mathrm{d}r \mathrm{d} \varphi =\] \[= \sigma \int_0^R r^3 \,\mathrm{d}r \int_0^{2\pi} \sin\varphi \cos \varphi \mathrm{d} \varphi\]Určeme hodnotu posledního uvedeného integrálu:
\[\int_0^{2 \pi} \cos \varphi \,\sin \varphi \,\mathrm{d}\varphi = \frac {1}{2} \int_0^{2 \pi} \sin {2 \varphi} \,\mathrm{d}\varphi = 0 .\]Je to určitý integrál z harmonické funkce počítaný přes celý násobek periody – tedy je integrál nulový, a proto také \(J_{xy}\) je nulový.
Vypočítali jsme všechny složky hledaného tenzoru setrvačnosti \(J\), už jen zbývá zapsat je do matice.
\[J = \begin{pmatrix} \frac {M R^2}{4} & 0 & 0 \\ 0 & \frac {M R^2}{4} & 0 \\ 0 & 0 & \frac {M R^2}{2} \end{pmatrix} = \frac {M R^2}{4} \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{pmatrix} \]Odpověď
Tenzor setrvačnosti \(J\) tenkého homogenního disku vzhledem k jeho hmotnému středu má tvar:
\[J = \frac {M R^2}{4} \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{pmatrix} . \]


