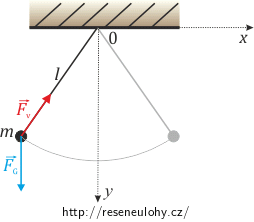
Matematické kyvadlo – síla závěsu

Úloha číslo: 947

Určete vazbovou sílu, kterou působí závěs matematického kyvadla na hmotný bod užitím Lagrangeových rovnic I. druhu.

Nápověda 1
Matematické kyvadlo je vlastně hmotný bod zavěšený na tuhém nehmotném závěsu. Určete síly, které na hmotný bod působí, a vazby, kterým je jeho pohyb podroben. Síly rozdělte na vtištěné a vazbové.
Řešení nápovědy 1
Nakreslíme si obrázek, kam zaneseme síly, které na hmotný bod působí:

Na hmotný bod působí vtištěná tíhová síla:
\[\vec{F}_G=(0,mg).\]
Zároveň na něj působí vazbová síla \(\vec{F_v}\), což je hledaná síla, kterou působí závěs.

Pohyb hmotného bodu je podroben vazbě:
\[G(x,y)=x^2+y^2-l^2=0.\tag{1}\]
Nápověda 2
Napište Lagrangeovy rovnice I. druhu. Které členy v těchto rovnicích odpovídají síle, kterou na hmotný bod působí závěs (tj. vazbové síle)?
Řešení nápovědy 2 – obecný tvar rovnic
Lagrangeovy rovnice I. druhu mají pro jeden hmotný bod v případě jediné vazby obecný tvar:
\[m\ddot{x}=F_{Gx}+\lambda\frac{\partial G} {\partial x},\] \[m\ddot{y}=F_{Gy}+\lambda\frac{\partial G}{\partial y},\]
kde \(F_{x}\) a \(F_{y}\) jsou složky vtištěné sily, v tomto případě tíhové síly. Složkám vazbové síly odpovídají druhé sčítance na pravých stranách rovnic.

Dosaďte konkrétní tvar vtištěné síly a vazby.
Řešení nápovědy 2 – dosazení
Po dosazení za složky vtištěné síly \(\vec{F_{G}}\) a výpočtu parciálních derivací vazby G získáváme:
\[m\ddot{x}=0+2\lambda x,\] \[m\ddot{y}=mg+2\lambda y.\]
Vazbová síla \(\vec{F_{v}}\) závěsu bude mít tedy tvar:
\[\vec{F}_{v}=(2\lambda x,2\lambda y).\]
Pro větší přehlednost upravíme obě Lagrangeovy rovnice vydělením hmotností m:
\[\ddot{x}=\frac{2\lambda}{m}x,\] \[\ddot{y}=\frac{2\lambda}{m}y+g.\]
Získali jsme vztahy pro zrychlení ve směru souřadnic x a y.

V obou rovnicích se vyskytuje stejný výraz \(\frac{2\lambda}{m}\), který můžeme označit např. jako \(\tilde\lambda\). Rovnice tedy nabývají tvaru:
\[\ddot{x}=\tilde\lambda x,\tag{2}\] \[\ddot{y}=\tilde\lambda y+g.\tag{3}\]
Nápověda 3
V předchozích nápovědách jsme získali tři rovnice:
\[x^2+y^2-l^2=0,\tag{1}\] \[\ddot{x}=\tilde\lambda x,\tag{2}\] \[\ddot{y}=\tilde\lambda y+g,\tag{3}\]
ve kterých vystupují 3 neznámé \(\tilde\lambda , x\) a y.

Pro výpočet vazbové síly závěsu nemusíme vyřešit celou soustavu, ale stačí nám nalézt řešení pro \(\tilde\lambda .\)

Způsobů existuje mnoho, různě komplikovaných. Zkuste následující:

a) Rovnici (2) vynásobte \(\dot{x}\) a sečtěte s rovnicí (3) vynásobenou \(\dot{y}\). Upravte.

b) Rovnici (2) vynásobte x a sečtěte s rovnicí (3) vynásobenou y.

Při úpravách využijte rovnici vazby (1).

Oba získané vztahy zkombinujte tak, abyste vyjádřili hledanou neznámou \(\tilde\lambda .\)
Užitečné vztahy
Při úpravách jsou užitečné následující vztahy:
\[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{1}{2}x^2\right)=x\dot{x},\] \[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{1}{2}\dot{x}^2\right)=\dot{x}\ddot{x}.\]
Dokažte si je přímým zderivováním vztahů na levé straně. Vztahy jsou uvedeny v proměnné x, ale je možné a vhodné použít je i pro y.
Řešení nápovědy 3 – úprava a)
Použijeme-li návodu z nápovědy 3, úpravou rovnic (2) a (3) získáváme rovnici:
\[\dot{x}\ddot{x}+\dot{y}\ddot{y}=\tilde\lambda x\dot{x}+\tilde\lambda y\dot{y}+g\dot{y}.\]
S využitím vztahů z oddílu Užitečné vztahy upravíme rovnici do tvaru:
\[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{1}{2}\dot{x}^2\right)+\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{1}{2}\dot{y}^2\right)=\tilde\lambda \frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{1}{2}{x}^2\right)+\tilde\lambda \frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{1}{2}{y}^2\right)+\frac{\mathrm{d}}{\mathrm{d}t}\left(gy\right).\]
Po vynásobení celé rovnice dvěma a sloučení podobných členů získáváme:
\[\frac{\mathrm{d}}{\mathrm{d}t}\left(\dot{x}^2+\dot{y}^2\right)=\tilde\lambda\frac{\mathrm{d}}{\mathrm{d}t}\left(x^2+y^2\right)+\frac{\mathrm{d}}{\mathrm{d}t}\left(2gy\right).\]
Z rovnice (1) vazby G víme, že \(x^2+y^2=l^2,\) což je konstanta. Takže celý první člen na pravé straně rovnice je roven nule, protože derivace konstanty je nula.

Převedením zbývajících členů na levou stranu rovnice a sloučením do společné derivace získáváme vztah:
\[\frac{\mathrm{d}}{\mathrm{d}t}\left(\dot{x}^2+\dot{y}^2-2gy\right)=0.\]
Z něho integrací získáme podmínku:
\[\dot{x}^2+\dot{y}^2-2gy=K,\tag{4}\]
kde K je konstanta.
Řešení nápovědy 3 – úprava b)
Jiným způsobem zkombinujeme rovnice (2) a (3) (viz nápověda):
\[x\ddot{x}+y\ddot{y}=\tilde\lambda x^2+\tilde\lambda y^2+gy.\]
Pomocí rovnice vazby \(x^2+y^2=l^2\) můžeme rovnici upravit:
\[x\ddot{x}+y\ddot{y}=\tilde\lambda l^2+gy.\tag{5}\]
Nyní zderivujme rovnici (1) vazby G podle času, dostaneme:
\[\frac{\mathrm{d}G}{\mathrm{d}t}=2x\dot{x}+2y\dot{y}=0.\]
Rovnici vydělíme dvěma a znovu derivujeme podle času. Získáváme:
\[\frac{1}{2}\frac{\mathrm{d}^2G}{\mathrm{d}t^2}=x\ddot{x}+\dot{x}^2+y\ddot{y}+\dot{y}^2=0.\]
Upravíme na tvar:
\[x\ddot{x}+y\ddot{y}=-(\dot{x}^2+\dot{y}^2).\]
Tu porovnáme s rovnicí (5) a získáme tak:
\[-(\dot{x}^2+\dot{y}^2)=\tilde\lambda l^2+gy.\tag{6}\]
Zkombinujte tento vztah se vztahem (4), který jsme získali v předchozím oddíle.
Řešení nápovědy 3 – vyjádření λ
V přechozích oddílech jsme získali tyto vztahy:
\[\dot{x}^2+\dot{y}^2-2gy=K,\tag{4}\] \[-(\dot{x}^2+\dot{y}^2)=\tilde\lambda l^2+gy.\tag{6}\]
Užitím těchto rovnic vyjádříme hledanou konstantu \(\tilde\lambda\):
\[\tilde\lambda =\frac{1}{l^2}(-K-3gy).\]
Pro λ tedy platí:
\[\lambda=\frac{m}{2}\tilde\lambda=\frac{m}{2l^2}(-K-3gy).\tag{7}\]
Nápověda 4
Určete konstantu K pomocí veličin, které se během pohybu zachovávají a lze je vyjádřit na základě počátečních podmínek. S její pomocí je již možno psát složky vazbové síly.
Řešení nápovědy 4
Pro konstantu K plyne z (4), že:
\[K=\dot{x}^2+\dot{y}^2-2gy=v^2-2gy.\]
V předchozí rovnici jsme využili vztah \(\dot{x}^2+\dot{y}^2=v^2\), který představuje druhou mocninu rychlosti v hmotného bodu.

Jelikož K je konstanta, bude souviset s nějakou veličinou, která je také konstantní. Takovou veličnou může být celková mechanické energie matematického kyvadla.

Ta má vzhledem k zavedení souřadnic tvar:
\[E=\frac{mv^2}{2}-mgy.\]
Porovnáním vztahů pro E a K zjistíme, že:
\[K=\frac{2E}{m}.\]
Připomeňme si vyjádření vazbové síly závěsu \(\vec{F_{v}}\) z nápovědy 2:
\[\vec{F}_{v}=(2\lambda x,2\lambda y).\]
Již nám nic nebrání v napsání složek vazbové síly. Postačí dosadit K do λ (rovnice (7)) a poté dosadit λ do složek vektoru síly:
\[F_{vx}=-(v^2+gy)\frac{m}{l^2}x=-(2E+3mgy)\frac{x}{l^2},\] \[F_{vy}=-(v^2+gy)\frac{m}{l^2}y=-(2E+3mgy)\frac{y}{l^2},\] \[\vec{F_{v}}=-\frac{(2E+3mgy)}{l^2}(x,y).\]
Celkové řešení
Na hmotný bod působí vtištěná tíhová síla:
\[\vec{F}_G=(0,mg).\]
Dále je jeho pohyb podroben vazbě:
\[G(x,y)=x^2+y^2-l^2=0.\tag{1}\]
Napíšeme Lagrangeovy rovnice I. druhu, které mají pro jeden hmotný bod v případě jediné vazby obecný tvar:
\[m\ddot{x}=F_{x}+\lambda\frac{\partial G} {\partial x},\] \[m\ddot{y}=F_{y}+\lambda\frac{\partial G}{\partial y},\]
kde \(F_{x}\) a \(F_{y}\) jsou složky výslednice vtištěných sil. Složkám vazbové síly odpovídají druhé členy na pravých stranách rovnice.

Vazbová síla \(\vec{F_{v}}\) závěsu bude mít tedy tvar:
\[\vec{F}_{v}=(2\lambda x,2\lambda y).\]
Dosadíme konkrétní tvar vtištěné síly a vazby G a obě Lagrangeovy rovnice vydělíme hmotností m:
\[\ddot{x}=\frac{2\lambda}{m}x,\] \[\ddot{y}=\frac{2\lambda}{m}y+g.\]
V obou rovnicích se vyskytuje stejný výraz \(\frac{2\lambda}{m}\), který můžeme označit např. jako \(\tilde\lambda\). Rovnice tedy nabývají tvaru:
\[\ddot{x}=\tilde\lambda x,\tag{2}\] \[\ddot{y}=\tilde\lambda y+g.\tag{3}\]
Pro výpočet vazbové síly závěsu nám stačí najít vyjádření pro neznámou \(\tilde\lambda .\)

Způsobů jejího nalezení je mnoho, různě obtížných. Podrobný popis jednoho z nich naleznete v nápovědě 3.

Vhodným zkombinováním obou Lagrangeových rovnic (2) a (3) s využitím derivace vazbové podmínky jsme v nápovědě 3 získali vztahy:
\[\dot{x}^2+\dot{y}^2-2gy=K,\tag{4}\] \[-(\dot{x}^2+\dot{y}^2)=\tilde\lambda l^2+gy,\tag{6}\]
ze kterých vyjádříme konstantu \(\tilde\lambda\):
\[\tilde\lambda =\frac{1}{l^2}(-K-3gy).\]
Pro λ tedy platí:
\[\lambda=\frac{m}{2}\tilde\lambda=\frac{m}{2l^2}(-K-3gy).\tag{7}\]
Pro konstantu K plyne z (4), že:
\[K=\dot{x}^2+\dot{y}^2-2gy=v^2-2gy,\]
kde v je rychlost hmotného bodu. Konstanta K musí souviset s něčím, co se během pohybu zachovává, zde se nabízí celková energie, kterou lze vyjádřit jako:
\[E=\frac{mv^2}{2}-mgy.\]
Pro konstantu K tedy dostáváme:
\[K=\frac{2}{m}E.\]
Připomeneme si vyjádření vazbové síly závěsu \(\vec{F_{v}}\):
\[\vec{F}_{v}=(2\lambda x,2\lambda y).\]
Již nám nic nebrání v napsání složek vazbové síly. Postačí dosadit K do λ a poté dosadit λ do složek vektoru vazbové síly:
\[F_{vx}=-(v^2+gy)\frac{m}{l^2}x=-(2E+3mgy)\frac{x}{l^2},\] \[F_{vy}=-(v^2+gy)\frac{m}{l^2}y=-(2E+3mgy)\frac{y}{l^2},\] \[\vec{F_{v}}=-\frac{(2E+3mgy)}{l^2}(x,y).\]
Odpověď
Vazbová síla, kterou působí závěs matematického kyvadla je:
\[\vec{F_{v}}=-\frac{(2E+3mgy)}{l^2}(x,y).\]
Odkazy
Problém řešení pohybu matematického kyvadla můžete řešit s použitím jiných postupů. Pohyb kyvadla je možné řešit užitím Lagrangeových rovnic II.druhu. Tento postup naleznete v úloze:
Matematické kyvadlo
Dalším příkladem může být hledání rovnovážné polohy matematického kyvadla. K tomu se užívá principu virtuální práce. Řešení naleznete v úloze:
Matematické kyvadlo – rovnovážné polohy
Komentář – velikost síly ve speciálním případě průchodu dolní polohou
Zajímavým příkladem může být rozebrání velikosti vazbové síly závěsu při průchodu dolní polohou.

Nalezli jsme obecné vyjádření této síly:
\[\vec{F_{v}}=\left(-(v^2+gy)\frac{m}{l^2}x,-(v^2+gy)\frac{m}{l^2}y\right).\]
Pro dolní polohu platí, že x = 0 a y = l. Tyto hodnoty proto dosadíme do obecného vyjádření. Získáváme:
\[\vec{F_{v}}=\left(0,-\frac{mv^2+mgl}{l}\right).\]
Vzhledem k zavedení souřadnic má výsledná vazbová síla směr vzhůru – to se shoduje s naším očekáváním.

Výsledek porovnejme s případem, kdy kyvadlo pouze visí na závěsu. V tomto případě by byla vazbová síla závěsu rovna reakci na sílu tíhovou, tedy:
\[\vec{F_{v_0}}=(0,-mg).\]
Z porovnání rovnic, je vidět, že v případě pohybu kyvadla působí závěs větší silou, než v případě kyvadla v klidu. Známe i velikost tohoto rozdílu:
\[|\vec{F_{v}}-\vec{F_{v_0}}|=\frac{mv^2}{l}.\]
Jedná se o velikost dostředivé síly při pohybu po kružnici. Pokud se hmotný bod pohybuje, potom na něj v nejnižší poloze působí závěs silou o velikosti součtu velikostí tíhové a dostředivé síly.