Tyč v dolíku

Úloha číslo: 1145

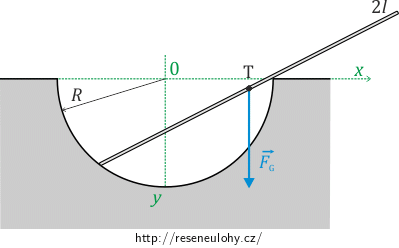
Nalezněte rovnovážnou polohu tyče délky 2l, která je umístěna do dolíku tvaru poloviny sféry s poloměrem R. Tření neuvažujte.

Nápověda 1
Pro určení rovnovážné polohy použijeme zobecněný princip virtuální práce. Je proto třeba znát virtuální posunutí a vtištěné síly, které na tyč působí. Napište působící vtištěné síly a určete jejich působiště.
Řešení nápovědy 1
Jedinou vtištěnou silou, jež na tyč působí, je tíhová síla, která vzhledem k zavedení souřadnic (viz obrázek) působí v kladném směru osy y a jejím působištěm je těžiště T:
\[\vec{F_G}=(0,mg).\]
Nápověda 2
Určete virtuální posunutí polohy těžiště tyče slučitelné s vazbami. Vzhledem k tomu, že tíhová síla působí ve směru osy y, postačí určit virtuální posunutí v tomto směru.
Řešení nápovědy 2 – volba parametru
Pro vyjádření virtuálního posunutí těžiště tyče ve směru y je nejprve nutné vyjádřit souřadnici y těžiště pomocí vhodného parametru, jehož hodnoty nejsou vazbou omezeny. K tomu je vhodné využít úhel α, který svírá tyč se svislým směrem.
Řešení nápovědy 2 – jak vyjádřit souřadnice těžiště
Souřadnici y těžiště T vyjádříme jako rozdíl:
\[y=v-u.\]
Vzdálenosti v a u jsou vyznačeny v obrázku.

Vyjádřete velikosti v a u v závislosti na úhlu α.
Řešení nápovědy 2 – vyjádření v
Vyjádření v provedeme na základě pravoúhlého trojúhelníka, který je určen body T, A a jeho pravý úhel svírají strany rovnoběžné s osami.Vzdálenost v bude mít tedy vyjádření:
\[v=l\cos{\alpha}.\]
Řešení nápovědy 2 – vyjádření u
Pro vyjádření délky u si nejprve určíme délku tyče uvnitř dolíku. K tomu využijeme žlutě označený rovnoramenný trojúhelník na obrázku. Velikost úhlu při vrcholu v počátku soustavy souřadnic je 2α a ramena trojúhelníka mají délku R. Délka části tyče uvnitř dolíku je tudíž rovna 2R sin α. Délka zbytku tyče je proto rovna 2l − 2R sin α.

Pro u bude proto platit vztah:
\[u=(2l-2R\sin{\alpha})\cos{\alpha}.\]
Řešení nápovědy 2 – souřadnice y těžiště
Dosadíme do rovnice:
\[y=v-u.\]
Tedy:
\[y=v-u=l\cos{\alpha}-(2l-2R\sin{\alpha})\cos{\alpha}=2R\sin{\alpha}\cos{\alpha}-l\cos{\alpha}=R\sin{2\alpha}-l\cos{\alpha.}\]
V poslední úpravě jsme použili vztah pro sinus dvojnásobného úhlu:
\[\sin{2\alpha}=2\sin{\alpha}\cos{\alpha}.\]
Řešení nápovědy 2 – virtuální posunutí
Virtuální posunutí souřadnice y v závislosti na úhlu α získáme jako:
\[\delta y=\frac{\mathrm{d}y}{\mathrm{d}\alpha}\delta\alpha.\]
Spočteme derivaci:
\[\frac{\mathrm{d}y}{\mathrm{d}\alpha}=\frac{\mathrm{d}(R\sin{2\alpha}-l\cos{\alpha})}{\mathrm{d}\alpha}=2R\cos{2\alpha}+l\sin{\alpha}.\]
Tedy:
\[\delta y=(2R\cos{2\alpha}+l\sin{\alpha})\delta\alpha.\]
Nápověda 3
Napište zobecněný princip virtuální práce nejprve obecně, poté dosaďte za sílu a virtuální posunutí a vyjádřete podmínku rovnováhy tyče v dolíku.
Užitečné vztahy
Při výpočtu se mohou hodit následující goniometrické vzorce:
\[\sin^2{\alpha}+\cos^2{\alpha}=1,\] \[\sin{2\alpha}=2\sin{\alpha}\cos{\alpha},\] \[\cos{2\alpha}=\cos^2{\alpha}-\sin^2{\alpha}.\]
Řešení nápovědy 3 – obecný tvar
Zobecněný princip virtuální práce zní takto:
\[\sum_{i=1}^N \vec{F_i}\cdot\delta\vec{r_i}=0,\]
kde \(\vec{F_i}\) jsou výslednice vtištěných sil na i-tý hmotný bod a \(\vec{r_i}\) jsou virtuální posunutí slučitelná s vazbami i-tého hmotného bodu.
Řešení nápovědy 3 – dosazení
V našem případě, kdy jediná nenulová složka vtištěné síly působí ve směru osy y, má zobecněný princip virtuální práce tvar:
\[F_y\delta y=0.\]
Dosadíme za sílu i virtuální posunutí (viz předchozí nápovědy):
\[mg(2R\cos{2\alpha}+l\sin{\alpha})\delta\alpha=0.\]
Rovnice platí pro libovolné virtuální posunutí δα, a proto ji jím můžeme vydělit. Dostáváme tak rovnici:
\[mg(2R\cos{2\alpha}+l\sin{\alpha})=0.\]
Rovnici dále vydělíme výrazem mg.
Řešení nápovědy 3 – vyjádření rovnováhy
Naším cílem je vyjádřit α. Rovnici tedy začneme upravovat pomocí goniometrických vztahů (viz užitečné vztahy uvedené výše):
\[2R\cos{2\alpha}+l\sin{\alpha}=2R\cos^2{\alpha}-2R\sin^2{\alpha}+l\sin{\alpha}=2R-4R\sin^2{\alpha}+l\sin{\alpha}=0.\]
Dospěli jsme ke kvadratické rovnici v neznámé sin α. Provedeme substituci z = sin α a upravíme na tvar:
\[z^2-\frac{l}{4R}z-\frac{1}{2}=0.\]
Rovnice má dvě řešení:
\[z_{1, 2}=\frac{l}{8R}\pm\frac{1}{2}\sqrt{\frac{l^2}{16R^2}+2}.\]
Řešení se znaménkem mínus nemá fyzikální smysl. Bude tedy stačit uvažovat jen jedno řešení. Po návratu k substituci tedy:
\[\sin{\alpha}=\frac{l}{8R}+\frac{1}{2}\sqrt{\frac{l^2}{16R^2}+2}.\]
Tato rovnice vyjadřuje podmínku rovnováhy.
Celkové řešení
Pro určení rovnovážné polohy tyče v dolíku užíváme zobecněný princip virtuální práce. Ten zní takto:
\[\sum_{i=1}^N \vec{F_i}\cdot\delta\vec{r_i}=0,\tag{1}\]
kde \(\vec{F_i}\) jsou výslednice vtištěných sil na i-tý hmotný bod a \(\vec{r_i}\) jsou virtuální posunutí slučitelná s vazbami i-tého hmotného bodu.

Jedinou vtištěnou silou působící na tyč je tíhová síla \(\vec{F_G}\), která vzhledem k zavedení souřadnic působí v kladném směru osy y a jejím působištěm je těžiště tyče T. Tedy:
\[\vec{F_G}=(0,mg).\]
Vzhledem k tomu, že x-ová složka síly je rovna nule, nemusíme vyjadřovat ani virtuální posunutí v této souřadnici.

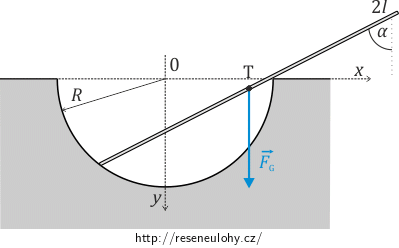
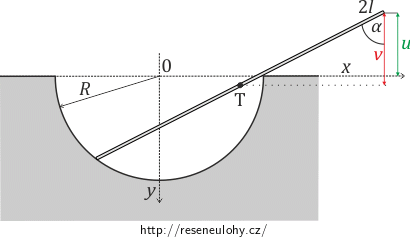
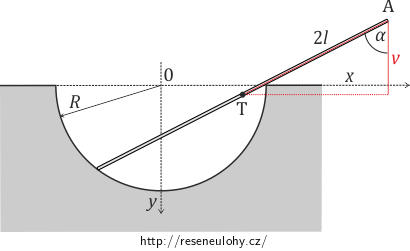
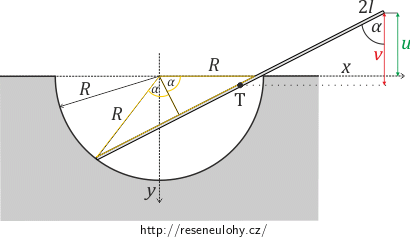
Potřebujeme tedy vyjádřit pouze virtuální posunutí vsouřadnici y. Souřadnici y těžiště vyjádříme v závislosti na úhlu α z geometrie úlohy (viz nápověda 2) jako:
\[y=R\sin{2\alpha}-l\cos{\alpha}.\]
Virtuální posunutí souřadnice y těžiště v závislosti na úhlu α má proto tvar:
\[\delta y=\frac{\mathrm{d}y}{\mathrm{d}\alpha}\delta\alpha=(2R\cos{2\alpha}+l\sin{\alpha})\delta\alpha.\]
Toto vyjádření dosadíme do rovnice (1):
\[F\delta y=mg(2R\cos{2\alpha}+l\sin{\alpha})\delta\alpha=0\]
a jejím řešením nalezneme podmínku rovnováhy:
\[\sin{\alpha}=\frac{l}{8R}\pm\frac{1}{2}\sqrt{\frac{l^2}{16R^2}+2}\ .\]
Řešení, kde se objevuje mínus, nemá fyzikální smysl.
Diskuze počtu řešení

Geometrie úlohy umožňuje pouze řešení pro úhel α v intervalu α = [0; π/2].

Ze dvou řešení rovnice rovnováhy tyče v dolíku jsme proto vybrali řešení ve tvaru:
\[\sin{\alpha}=\frac{l}{8R}+\frac{1}{2}\sqrt{\frac{l^2}{16R^2}+2}\ .\]
Jelikož hodnota funkce sinus nemůže být větší než jedna, získáme hraniční podmínku pro vztah mezi délkou poloviny tyče l a poloměrem R dosazením hodnoty sin α = 1:
\[1=\frac{l}{8R}+\frac{1}{2}\sqrt{\frac{l^2}{16R^2}+2}\ .\]
První člen na pravé straně převedeme vlevo a rovnici umocníme na druhou:
\[1-\frac{l}{4R}+\frac{l^2}{64R^2}=\frac{l^2}{64R^2}+\frac{1}{2}.\]
Členy v druhých mocninách jsou na obou stranách stejné, proto je můžeme odečíst a získáváme tak:
\[1-\frac{l}{4R}=\frac{1}{2}.\]
Po úpravě získáme podmínku ve tvaru:
\[l=2R.\]
Z této podmínky vidíme, že řešení existuje pouze v případě, kdy je tyč délky 2l menší než čtyřnásobek poloměru R. Pokud by délka tyče byla větší, dostalo by se těžiště tyče mimo dolík a tyč by z dolíku vypadla.
Odpověď
Podmínka rovnováhy tyče v dolíku je:
\[\sin{\alpha}=\frac{l}{8R}+\frac{1}{2}\sqrt{\frac{l^2}{16R^2}+2}\ ,\]
kde \(\alpha\) je úhel, který svírá tyč s osou y, R je poloměr dolíku a l je polovina délky tyče.

Řešení platí za podmínky:
\[l\le2R.\]
Není-li podmínka splněna, rovnovážná poloha neexistuje.