Sbírka řešených úloh

n kuliček spojených n+1 pružinami

Úloha číslo: 2264

Mějme \(n\) kuliček o hmotnosti \(m\) mezi sebou spojených pružinami, které mají všechny stejnou tuhost \(k\) a klidovou délku \(d\), tak, že leží v jedné přímce. Dále jsou na obou koncích připevněny pružinami k nehybným stěnám, které od sebe mají vzdálenost \(\left( n+1 \right) d\).

Najděte pro naše kuličky k nim příslušné pohybové rovnice. Najděte maticovou pohybovou rovnici popisující pohyb celé soustavy.

• Nápověda 1

  Najděte vhodné souřadnice pro popis pohybu našich kuliček.

• Řešení – Nápověda 1

  Jako soustavu souřadnic zvolíme přímku, která je rovnoběžná s pružinami a každé \(i\)-té kuličce přiřadíme souřadnici \(x_i\).

  

  Polohu levé stěny, tedy bod \(x_0\) zvolme za počátek osy, tedy \(x_0 = 0\). Potom je poloha pravé stěny \(x_{n+1} = \left( n+1 \right)d\).

• Nápověda 2

  Najděte vztahy pro kinetickou energii \(T\) soustavy a pro potenciální energii \(V\) soustavy. Určete lagrangián \(L\).

• Řešení – Nápověda 2

  Začněme určením celkové kinetické energie \(T\). Tu získáme jako součet kinetických energií \(T_i\) jednotlivých kuliček.

  \[T = \sum_{i=1}^n {T_i} = \sum_{i=1}^n {\frac{1}{2} m \dot{x_i}^2}\]

  Nyní se podíváme na potenciální energii \(V\). V soustavě máme \(n+1\) pružin.

  

  Očíslujme si pružiny zleva doprava od \(0\) do \(n\). Délka nulté pružiny je \(x_1 - x_0\). Potom pro potenciální energii nulté pružiny \(V_0\) platí:

  \[V_0 = \frac{1}{2} k \left[ \left( x_1 - x_0 \right) - d \right]^2 \, .\]

  Pro \(i\)-tou pružinu platí velice obdobný vztah.

  \[V_i = \frac{1}{2} k \left[ \left( x_{i+1} - x_i \right) - d \right]^2 \, .\]

  Celková potenciální energie \(V\) je součtem jednotlivých dílčích potenciálních energií.

  \[V = \sum_{i=0}^n \frac{1}{2} k \left[ \left( x_{i+1} - x_i \right) - d \right]^2 \, .\] \[V = \frac{1}{2} k \sum_{i=0}^n \left[ \left( x_{i+1} - x_i \right)^2 - 2 d \left( x_{i+1} - x_i \right) + d^2 \right] = \frac{1}{2} k \sum_{i=0}^n {\left( x_{i+1} - x_i \right)^2} - d k \sum_{i=0}^n {\left( x_{i+1} - x_i \right)} + \frac{1}{2} k d^2\]

  Podívejme se na druhou uvedenou sumu.

  \[\sum_{i=0}^n {\left( x_{i+1} - x_i \right)} = x_1 - x_0 + x_2 - x_1 + x_3 - x_2 + ... + x_{n+1}- x_n = x_{n+1} - x_0 = d \left( n+1 \right)\] \[V = \frac{1}{2} k \sum_{i=0}^n {\left( x_{i+1} - x_i \right)^2} - d^2 k \left( n+1 \right) + \frac{1}{2} k d^2\]

  Protože poslední dva členy v potenciálu \(V\) jsou konstantní, tedy nebudou po derivacích hrát žádnou roli, označme je prostě souhrnně jako konstantu \(C\).

  \[V = \frac{1}{2} k \sum_{i=0}^n {\left( x_{i+1} - x_i \right)^2} + C\]

  Teď již jen spočítáme lagrangián \(L = T - V\).

  \[L = \frac{1}{2} m \sum_{i=1}^n {\dot{x_i}^2} - \frac{1}{2} k \sum_{i=0}^n {\left( x_{i+1} - x_i \right)^2} - C\]

• Nápověda 3

  Použijte Lagrangeovy rovnice druhého druhu. Najděte pohybové rovnice pro jednotlivé kuličky.

• Řešení – Nápověda 3

  Použijeme Lagrangeovy rovnice druhého druhu.

  \[\frac{\partial}{\partial t} \left( \frac{\partial L}{\partial \dot{x_i}} \right) - \frac{\partial L}{\partial x_i} = 0\]

  Teď si spočítáme všechny potřebné derivace.

  \[\frac{\partial L}{\partial \dot{x_i}} = \frac{\partial}{\partial \dot{x_i}} \left( \frac{1}{2} m \sum_{i=1}^n {\dot{x_i}^2} - \frac{1}{2} k \sum_{i=0}^n {\left( x_{i+1} - x_i \right)^2} + C \right) = m \dot{x_i}\] \[\frac{\mathrm{d}}{\mathrm{d} t} \left( \frac{\partial L}{\partial \dot{x_i}} \right) = m \ddot{x_i}\] \[\frac{\partial L}{\partial x_i} = \frac{\partial}{\partial x_i} \left( \frac{1}{2} m \sum_{i=1}^n {\dot{x_i}^2} - \frac{1}{2} k \sum_{i=0}^n {\left( x_{i+1} - x_i \right)^2} + C \right) = \frac{\partial}{\partial x_i} \left( - \frac{1}{2} k \sum_{i=0}^n {\left( x_{i+1} - x_i \right)^2} \right) \]

  Podívejme se, jak vypadá prvních několik členů poslední sumy.

  \[\sum_{i=0}^n {\left( x_{i+1} - x_i \right)^2} = \left( x_1 - x_0 \right)^2 + \left( x_2 - x_1 \right)^2 + \left( x_3 - x_2 \right)^2 + \cdots = \] \[= x_1^2 + x_2^2 - 2 x_1 x_2 + x_1^2 + x_3^2 - 2 x_3 x_2 + x_2^2 + \cdots\]

  Co získáme po zderivování této sumy např. podle \(x_2\)?

  \[\frac{\partial}{\partial x_2} \left( \sum_{i=0}^n {\left( x_{i+1} - x_i \right)^2} \right) = \frac{\partial}{\partial x_2} \left( x_1^2 + x_2^2 - 2 x_1 x_2 + x_1^2 + x_3^2 - 2 x_3 x_2 + x_2^2 + \cdots \right) = \] \[= \frac{\partial}{\partial x_i} \left( 2 x_2^2 - 2 x_2 x_1 - 2 x_2 x_3 \right) = 4 x_2 - 2 x_1 - 2 x_3\]

  A po lehkém zobecnění zpět na derivaci podle \(x_i\) dostaneme:

  \[\frac{\partial L}{\partial x_i} = \frac{\partial}{\partial x_i} \left( - \frac{1}{2} k \sum_{i=0}^n {\left( x_{i+1} - x_i \right)^2} \right) = - k\left( 2 x_i - x_{i-1} - x_{i+1} \right) \, .\]

  Nyní dosaďme do Lagrangeových rovnic a dostaneme pohybovou rovnici pro \(i\)-tou kuličku.

  \[m \ddot{x_i} + k\left( 2 x_i - x_{i-1} - x_{i+1} \right) = 0\] \[m \ddot{x_i} + 2 k x_i = k x_{i-1} + k x_{i+1}\]

  Přesně jak bychom očekávali, lze vidět, že pohyb \(i\)-té kuličky je skrze tuhost přilehlých pružin svázán s okolními dvěma kuličkami.

• Nápověda 4

  Zapište lagrangián pomocí matic.

  Pokuste se zapsat Lagrangeovy rovnice pro všechny kuličky jednou maticovou rovnicí.

• Řešení – Nápověda 4

  Připomeňme si, jak vypadá lagrangián \(L\) pro naše kuličky.

  \[L = \frac{1}{2} m \sum_{i=1}^n {\dot{x_i}^2} - \frac{1}{2} k \sum_{i=0}^n {\left( x_{i+1} - x_i \right)^2} - C\]

  Pro kinetickou energii \(T\) platí vztah:

  \[T = \frac{1}{2} m \sum_{i=1}^n {\dot{x_i}^2} \, .\]

  Uvědomíme-li si, že \(\sum_{i=1}^n {\dot{x_i}^2}\) je vlastně jen zápis skalárního součinu vektorů \(\vec{\dot{x}} \cdot \vec{\dot{x}}\), kde \(\vec{\dot{x}^T} = \begin {pmatrix} \dot{x_1}, & \dot{x_2}, & \dot{x_3}, & \cdots & \dot{x_n}, & \dot{x_{n+1}} \end{pmatrix}\), můžeme potom kinetickou energii \(T\) psát následovně.

  \[T = \frac{1}{2} m \vec{\dot{x}^T} \cdot \vec{\dot{x}}\]

  Po dohodě, že přestaneme psát šipky u vektorů \(x\) a \(\dot x\) budeme maticově kinetickou energii zapisovat takto:

  \[T = \frac{1}{2} m \dot{x}^T \mathbb{E} \, \dot{x} \, ,\]

  kde \(\mathbb{E}\) je jednotková matice.

  Velice podobně se popereme s potenciální energií \(V\).

  \[V = \frac{1}{2} k \sum_{i=0}^n {\left( x_{i+1} - x_i \right)^2}\]

  Opět se budeme soustředit na danou sumu a rozepíšeme si několik členů.

  \[\sum_{i=0}^n \left( x_{i+1} - x_i \right)^2 = \left( x_1 - x_0 \right)^2 + \left( x_2 - x_1 \right)^2 + \left( x_3 - x_2 \right)^2 + \cdots + \left( x_{n+1} - x_n \right)^2= \] \[= x_1^2 + x_2^2 - 2 x_1 x_2 + x_1^2 + x_3^2 - 2 x_3 x_2 + x_2^2 + \cdots + x_{n+1}^2 - 2 x_{n+1} x_n + x_n^2 = \] \[= 2 x_1^2 - x_1 x_2 - x_2 x_1 + 2 x_2^2 - x_2 x_3 - x_3 x_2 + 2 x_3^2 + \cdots + 2 x_n^2 - x_n x_{n+1} - x_{n+1} x_n + x_{n+1}^2=\] \[= \begin {pmatrix} x_1, & x_2, & x_3, & \cdots & x_n , & x_{n+1} \end{pmatrix} \begin {pmatrix} 2 & -1 & 0 & 0 & \cdots & 0 \\ -1 & 2 & -1 & 0 & \cdots & 0 \\ 0 & -1 & 2 & -1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \ddots \\ 0 & 0 & \cdots & \cdots & -1 & 1 \end{pmatrix} \begin {pmatrix} x_1 \\ x_2 \\ x_3 \\ \vdots \\ x_n \\ x_{n+1} \end{pmatrix} = x^T \mathbb{V} x \]

  Potenciální energii \(V\) tedy můžeme psát jako:

  \[V = \frac{1}{2} k x^T \mathbb{V} x \, ,\]

  kde \(\mathbb{V}\) je matice, která má na hlavní diagonále dvojky, nad a pod hlavní diagonálou mínus jedničky a na všech ostatních pozicích nuly.

  Lagrangián \(L\) tedy maticově zapíšeme jako:

  \[L = \frac{1}{2} m \dot{x}^T \mathbb{E} \, \dot{x} - \frac{1}{2} k x^T \mathbb{V} x - C \, .\]

  Spočítejme si derivace potřebné v Lagrangeových rovnicích.

  \[\frac{\partial L}{\partial \dot{x}} = \frac{1}{2} m \left( \mathbb E \dot x + \dot{x}^T \mathbb E \right) = \frac{1}{2} m \left( \mathbb E \dot x + \mathbb E \dot x \right) = m \mathbb E \dot x\] \[\frac{\partial L}{\partial x} = - \frac{1}{2} k \left( \mathbb V x + x^T \mathbb V \right) = - k \mathbb V x\]

  Pohybová rovnice našich kuliček v maticové zápisu vypadá takto:

  \[m \mathbb E \ddot x + k \mathbb V x = 0 \, .\]

  Máme-li na paměti poznatky z lineární algebry a interpretujeme si matici jako schematický zápis soustavy rovnic, pak by měl \(i\)-tý řádek naší maticové rovnice odpovídat rovnici pro pohyb i-tého bodu.

  \[m \ddot{x_i} + k\left( 2 x_i - x_{i-1} - x_{i+1} \right) = 0\]

  Toto je stejný výsledek, jaký jsme získali v Řešení – Nápověda 3.

• Celkové řešení

  Nejprve zvolíme soustavu souřadnic. Pohyb kuliček bude jednodimenzionální, tedy vystačíme s jednou souřadnicí. Označíme ji \(x\) a její souřadnicová osa odpovídá přímce procházející středem všech kuliček, podél níž se pohybují (viz následující obrázek).

  

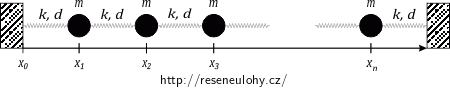
  Počátek souřadnicové osy volíme na levé stěně, tedy v bodě \(x_0\).

  Protože budeme k vyřešení úlohy využívat Lagrangeův formalismus, musíme nejprve určit kinetickou a potenciální energii \(T\) a \(V\).

• Odpověď

  Hledaná pohybová rovnice pro \(i\)-tou kuličku má tvar:

  \[m \ddot{x_i} + k\left( 2 x_i - x_{i-1} - x_{i+1} \right) = 0 \, .\]

  V maticovém zápisu bude mít tato rovnice tvar:

  \[m \mathbb E \ddot x + k \mathbb V x = 0 \, ,\]

  kde \(\mathbb E\) je jednotková matice, \(\mathbb V\) je matice

  \[\mathbb V = \begin {pmatrix} 2 & -1 & 0 & 0 & \cdots & 0 \\ -1 & 2 & -1 & 0 & \cdots & 0 \\ 0 & -1 & 2 & -1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \ddots \\ 0 & 0 & \cdots & \cdots & -1 & 1 \end{pmatrix}\]

  a \(x\) je vektor \(\begin {pmatrix} x_1, & x_2, & x_3, & \cdots & x_n , & x_{n+1} \end{pmatrix}\).