Hmotná pružina

Úloha číslo: 1250

Řešte pohyb závaží o hmotnosti m, které je zavěšené na homogenní pružině o tuhosti k, rovnovážné délce l a hmotnosti M.

Použijte Lagrangeovy rovnice II. druhu.
Použijte Hamiltonovy kanonické rovnice.

Nápověda 1
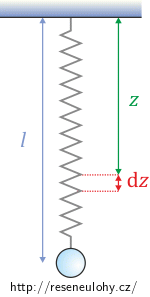
Nakreslete si obrázek situace, rozmyslete, kolik má úloha stupňů volnosti, a vhodně zvolte souřadnice.
Řešení nápovědy 1
Úloha má jeden stupeň volnosti. Pohyb závaží popíšeme pomocí souřadnice x, jejíž zavedení vidíte na obrázku.
Nápověda 2
Vyjádřete kinetickou a potenciální energii systému. Nezapomeňte, že je pružina hmotná, a tedy musíte uvažovat nejenom potenciální energii pružnosti, ale i další její energie.
Řešení nápovědy 2
Potenciální energie V se bude skládat ze tří složek:
- tíhové potenciální energie závaží V_m,
- potenciální energie pružnosti pružiny V_p,
- tíhové potenciální energie pružiny V_M.
Tíhová potenciální energie závaží V_m o hmotnosti m má tvar:
\[V_m=-mgx.\]
S narůstající souřadnicí x se potenciální energie zmenšuje, proto zde vystupuje znaménko mínus.

Potenciální energii pružnosti V_p získáme jako:
\[V_p=\frac{1}{2}k(x-l)^2.\]
Těžiště pružiny je v polovině její délky. Navíc předpokládáme, že se protáhne ve všech místech stejně, tedy zanedbáváme mírně nehomogenní lineární hustotu protažené pružiny. Tíhovou potenciální energii pružiny V_M o hmotnosti M vyjádříme vzhledem k zavedení souřadnice x jako:
\[V_M=-\frac{1}{2}Mgx.\]
Celková potenciální energie systému V má vyjádření:
\[V=V_m+V_p+V_M=-mgx+\frac{1}{2}k(x-l)^2-\frac{1}{2}Mgx.\]
Kinetická energie bude mít dvě složky:
- kinetická energie posuvného pohybu závaží T_m,
- kinetická energie posuvného pohybu pružiny T_M.
Kinetická energie posuvného pohybu závaží T_m má tvar:
\[T_m=\frac{1}{2}m\dot{x}^2.\]
Nyní odvodíme kinetickou energii posuvného pohybu pružiny T_M.

Pro zjištění kinetické energie T_M budeme muset vysčítat všechny příspěvky ke kinetické energii.

Představme si element pružiny dz, jehož vzdálenost od upevnění pružiny je z. Délku pružiny označme l (viz obrázek).

Pro element hmotnosti dM vzhledem k předpokladu lineární hustoty pružiny platí:
\[\mathrm{d}M=M\frac{\mathrm{d}z}{l}.\]
Výchylka elementu x_z z jeho rovnovážné polohy je vzhledem k předpokládanému stejnoměrnému protažení úměrná poměru vzdálenosti elementu od uchycení pružiny z a délky tyče l. Má tedy tvar:
\[x_z=x\frac{z}{l}.\]
Časovou derivací tohoto vztahu získáme rychlost pohybu tohoto elementu pružiny:
\[\dot{x}_z=\dot{x}\frac{z}{l}.\]
Element kinetické energie T_M získáme jako:
\[\mathrm{d}T_M=\frac{1}{2}{\dot{x}}^2_z\mathrm{d}M.\]
Dosadíme za element hmotnosti dM a rychlost elementu \(\dot{x}_z\):
\[\mathrm{d}T_M=\frac{1}{2}\mathrm{d}M{\dot{x}}^2_z=\frac{1}{2}M\frac{\mathrm{d}z}{l}\dot{x}^2\frac{z^2}{l^2}=\frac{1}{2}M\dot{x}^2\frac{z^2}{l^3}\mathrm{d}z.\]
Integrací podél celé pružiny dostáváme kinetickou energii posuvného pohybu pružiny T_M:
\[T_M=\int^l_0\frac{1}{2}M\dot{x}^2\frac{z^2}{l^3}\mathrm{d}z=\frac{1}{2}M\frac{\dot{x}^2}{l^3}\int^l_0z^2\mathrm{d}z=\frac{1}{6}M\dot{x}^2.\]
Celkovou kinetickou energii T tak můžeme vyjádřít jako:
\[T=T_m+T_M=\frac{1}{2}(m+\frac{1}{3}M)\,\dot{x}^2.\]
Nápověda 3 a)
Napište Lagrangeovu funkci L a Lagrangeovy rovnice II. druhu.

Lagrangeova rovnice pro úlohu s jedním stupněm volnosti má tvar:
\[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial{L}}{\partial{\dot{x}}}\right)-\frac{\partial{L}}{\partial{x}}=0,\]
kde x je zobecněná souřadnice a \(\dot{x}\) je zobecněná rychlost.
Řešení nápovědy 3 a)
Lagrangián L získáme pomocí kinetické energie T a potenciální energie V:
\[L=T-V=\frac{1}{2}(m+\frac{1}{3}M)\dot{x}^2-\frac{1}{2}k(x-l)^2+\frac{1}{2}Mgx+mgx.\]
Nejdříve určíme parciální derivace lagrangiánu L podle zobecněné souřadnice a rychlosti:
\[\frac{\partial{L}}{\partial{x}}=-k(x-l)+(\frac{1}{2}M+m)g,\] \[\frac{\partial{L}}{\partial{\dot{x}}}=(m+\frac{1}{3}M)\dot{x}.\]
Poslední rovnost ještě zderivujeme podle času a získáme:
\[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial{L}}{\partial{\dot{x}}}\right)=(m+\frac{1}{3}M)\ddot{x}.\]
Nyní již můžeme sestrojit Lagrangeovu rovnici II. druhu ve tvaru:
\[(m+\frac{1}{3}M)\ddot{x}+k(x-l)-(\frac{1}{2}M+m)g=0.\]
Nápověda 3 b)
Napište Hamiltonovu funkci H a Hamiltonovy kanonické rovnice.

Hamiltonovy kanonické rovnice mají obecně tvar:
\[\dot{q_i}=\frac{\partial{H}}{\partial{p_i}},\] \[\dot{p_i}=-\frac{\partial{H}}{\partial{q_i}},\] \[\frac{\partial{L}}{\partial{t}}=-\frac{\partial{H}}{\partial{t}}.\]
Jak jsme zjistili v minulé nápovědě, lagrangián L není explicitně závislý na čase. Totéž můžeme říci i o hamiltoniánu H. Poslední rovnice je tedy automaticky splněna.

Hamiltonián H je funkcí zobecněných souřadnic q_i a zobecněných hybností p_i. Zobecněné hybnosti jsou definovány pomocí vzorce:
\[p_i=\frac{\partial{L}}{\partial{\dot{q_i}}}.\]
Řešení nápovědy 3 b)
Máme jednu zobecněnou souřadnici x. Jedinou zobecněnou hybnost p tak spočítáme jako:
\[p=\frac{\partial{L}}{\partial{\dot{x}}}=(m+\frac{1}{3}M)\,\dot{x}.\]
Protože lagrangián L nezávisí explicitně na čase, hamiltonián H můžeme napsat jako celkovou mechanickou energii:
\[H=T+V=\frac{1}{2}(m+\frac{1}{3}M)\,\dot{x}^2+\frac{1}{2}k(x-l)^2-(\frac{1}{2}M+m)gx.\]
Po vyjádření v přirozených proměnných:
\[H=\frac{p^2}{2(m+\frac{1}{3}M)}+\frac{1}{2}k(x-l)^2-(\frac{1}{2}M+m)gx.\]
Hamiltonovy kanonické rovnice nabývají v našem případě tvaru:
\[\dot{x}=\frac{\partial{H}}{\partial{p}}=\frac{p}{m+\frac{1}{3}M},\] \[\dot{p}=-\frac{\partial{H}}{\partial{x}}=-k(x-l)+(\frac{1}{2}M+m)g.\]
Nápověda 4
Řešte Lagrangeovu pohybovou rovnici:
\[(m+\frac{1}{3}M)\,\ddot{x}+k(x-l)-(\frac{1}{2}M+m)g=0.\]
K řešení můžete využít Kladka na pružině, Komentář – řešení pohybové rovnice.
Řešení nápovědy 4
Pohybovou rovnici upravíme do tvaru:
\[\ddot{x}+\frac{k}{m+\frac{1}{3}M}x=\frac{kl+(\frac{1}{2}M+m)g}{m+\frac{1}{3}M}.\]
Jedná se o rovnici pro harmonický oscilátor.

Řešení této rovnice známe, podívejte se na úlohu Kladka na pružině, Komentář – řešení pohybové rovnice.

Řešení má tedy tvar:
\[x=\left[x_0-\left(l+(\frac{1}{2}M+m)\frac{g}{k}\right)\right]\cos{\omega t}+\frac{v_0}{\omega}\sin{\omega t}+l+(\frac{1}{2}M+m)\frac{g}{k},\]
kde x₀ je počáteční výchylka, v₀ počáteční rychlost a ω úhlová frekvence definovaná vztahem:
\[\omega=\sqrt{\frac{k}{m+\frac{1}{3}M}}.\]
Závaží tedy bude kmitat s danou frekvencí ω. Tato frekvence je menší, než je tomu v případě nemhotné pružiny.
Ekvivalence Lagrangeových a Hamiltonových rovnic – nápověda
Lagrangeovu rovnic II. druhu jsme získali ve tvaru:
\[(m+\frac{1}{3}M)\ddot{x}+k(x-l)-(\frac{1}{2}M+m)g=0.\tag{1}\]
Hamiltonovy kanonické rovnice mají tvar:
\[\dot{x}=\frac{p}{(m+\frac{1}{3}M)},\tag{2}\] \[\dot{p}=-k(x-l)+(\frac{1}{2}M+m)g.\tag{3}\]
Nyní ukažte ekvivalenci těchto rovnic. Díky tomu nebude nutné Hamiltonovy kanonické rovnice řešit, protože jejich řešení bude stejné, jako řešení Lagrangeovy rovnice II. druhu.
Ekvivalence Lagrangeových a Hamiltonových rovnic – řešení
Rovnici (2) nejprve zderivujeme podle času:
\[\ddot{x}=\frac{\dot{p}}{m+\frac{1}{3}M}.\]
Do této rovnice dosadíme za \(\dot{p}\) z rovnice (3):
\[\ddot{x}=\frac{-k(x-l)+(\frac{1}{2}M+m)g}{m+\frac{1}{3}M}.\]
Vynásobením rovnice výrazem \(m+\frac{1}{3}M\) a převedením všech členů na jednu stranu získáváme:
\[(m+\frac{1}{3}M)\ddot{x}+k(x-l)-(\frac{1}{2}M+m)g=0,\]
což je Lagrangeova rovnice II. druhu (1).

Zjistili jsme, že Lagrangeův i Hamiltonův přístup dávají ekvivalentní pohybové rovnice.
Celkové řešení
Úloha má jeden stupeň volnosti. Pohyb závaží popíšeme pomocí souřadnice x, jejíž zavedení vidíte na obrázku.

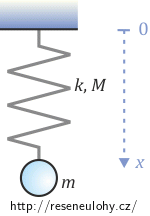
Celková potenciální energie systému V se skládá z tíhové potenciální energie závaží V_m, potenciální energie pružnosti pružiny V_p, tíhové potenciální energie pružiny V_M, a má vyjádření:
\[V=V_m+V_p+V_M=-mgx+\frac{1}{2}k(x-l)^2-\frac{1}{2}Mgx.\]
Celková kinetická energie systému T se skládá z kinetické energie posuvného pohybu závaží T_m a kinetické energie posuvného pohybu pružiny T_M:
\[T=T_m+T_M=\frac{1}{2}(m+\frac{1}{3}M)\dot{x}^2.\]
Podrobné odvození naleznete v nápovědě 2.

Pro lagrangián L tedy platí:
\[L=T-V=\frac{1}{2}(m+\frac{1}{3}M)\dot{x}^2-\frac{1}{2}k(x-l)^2+\frac{1}{2}Mgx+mgx.\]
Lagrangeova rovnice pro úlohu s jedním stupněm volnosti má tvar:
\[\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial{L}}{\partial{\dot{x}}}\right)-\frac{\partial{L}}{\partial{x}}=0,\]
kde x je zobecněná souřadnice a \(\dot{x}\) je zobecněná rychlost.

V našem případě získáváme:
\[(m+\frac{1}{3}M)\ddot{x}+k(x-l)-(\frac{1}{2}M+m)g=0.\]
Abychom mohli vyjádřit Hamiltonovu funkci H v jejích přirozených proměnných, spočítáme zobecněnou hybnost p jako:
\[p=\frac{\partial{L}}{\partial{\dot{x}}}=(m+\frac{1}{3}M)\dot{x}.\]
Protože lagrangián L nezávisí explicitně na čase, hamiltonián H získáme jako celkovou mechanickou energii:
\[H=T+V=\frac{1}{2}(m+\frac{1}{3}M)\dot{x}^2+\frac{1}{2}k(x-l)^2-(\frac{1}{2}M+m)gx,\]
a vyjádříme jej pomocí zobecněné souřadnice x a zobecněné hybnosti p:
\[H=\frac{p^2}{2(m+\frac{1}{3}M)}+\frac{1}{2}k(x-l)^2-(\frac{1}{2}M+m)gx.\]
Hamiltonovy kanonické rovnice mají obecně tvar:
\[\dot{q_i}=\frac{\partial{H}}{\partial{p_i}},\] \[\dot{p_i}=-\frac{\partial{H}}{\partial{q_i}},\] \[\frac{\partial{L}}{\partial{t}}=-\frac{\partial{H}}{\partial{t}}.\]
Poslední uvedená rovnice je díky nezávislosti hamiltoniánu H na čase automaticky splněna a v našem případě tak zbylé rovnice nabývají tvaru:
\[\dot{x}=\frac{p}{m+\frac{1}{3}M},\] \[\dot{p}=-k(x-l)+(\frac{1}{2}M+m)g.\]
Hamiltonvy kanonické rovnice a Lagrangeovy rovnice II. jsou ekvivalentní, jak se můžete přesvědčit v oddíle Ekvivalence Lagrangeových a Hamiltonových rovnic. K popsání pohybu systému využijeme tvaru Lagrangeovy rovnice:
\[(m+\frac{1}{3}M)\ddot{x}+k(x-l)-(\frac{1}{2}M+m)g=0.\]
Upravíme ji na tvar:
\[\ddot{x}+\frac{k}{m+\frac{1}{3}M}x=\frac{kl+(\frac{1}{2}M+m)g}{m+\frac{1}{3}M},\]
což je dobře známá rovnice pro harmonický oscilátor.

K jejímu řešení dospějete pomocí Kladka na pružině, Komentář – řešení pohybové rovnice:
\[x=\left[x_0-\left(l+(\frac{1}{2}M+m)\frac{g}{k}\right)\right]\cos{\omega t}+\frac{v_0}{\omega}\sin{\omega t}+l+(\frac{1}{2}M+m)\frac{g}{k},\]
kde x₀ je počáteční výchylka, v₀ počáteční rychlost a ω úhlová frekvence definovaná vztahem:
\[\omega=\sqrt{\frac{k}{m+\frac{1}{3}M}}.\]
Závaží tedy bude kmitat s danou frekvencí ω. Tato frekvence je menší, než je tomu v případě nemhotné pružiny.
Odpověď
Lagrangeova rovnice II. druhu má tvar:
\[(m+\frac{1}{3}M)\ddot{x}+k(x-l)-(\frac{1}{2}M+m)g=0.\]
Hamiltonovy kanonické rovnice mají tvar:
\[\dot{x}=\frac{p}{m+\frac{1}{3}M},\] \[\dot{p}=-k(x-l)+(\frac{1}{2}M+m)g.\]
Pohyb systému popisuje rovnice:
\[x=\left[x_0-\left(l+(\frac{1}{2}M+m)\frac{g}{k}\right)\right]\cos{\omega t}+\frac{v_0}{\omega}\sin{\omega t}+l+(\frac{1}{2}M+m)\frac{g}{k},\]
kde x₀ je počáteční výchylka, v₀ počáteční rychlost a ω úhlová frekvence definovaná vztahem:
\[\omega=\sqrt{\frac{k}{m+\frac{1}{3}M}}.\]
Závaží tedy bude kmitat s danou frekvencí ω. Tato frekvence je menší, než je tomu v případě nehmotné pružiny.