Sbírka řešených úloh

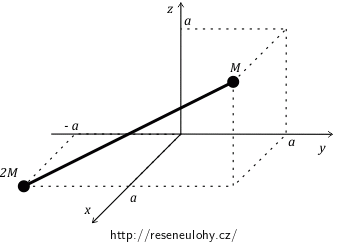
Tenzor setrvačnosti činky – hledání hlavních os

Úloha číslo: 2252

• Nápověda 1

  Zakreslete si situaci.

  Rozvažte, jakých vztahů budete užívat a jaké všechny veličiny budete potřebovat k určení tenzoru setrvačnosti.

• Řešení – Nápověda 1

  

  Pro určení jednotlivých složek tenzoru setrvačnosti \(J_{jk}\) soustavy \(N\) hmotných bodů platí vztah:

  \[J_{jk}= \sum_{i=1}^{N}{ m_{(i)}( \delta_{jk} \, r_{(i)}^2 - x_{(i)j} \, x_{(i)k} )}\]

  kde \(i\) indexuje hmotné body o hmostnosti \(m_i\), \(r_i\) je vzdálenost \(i\)-tého bodu od počátku soustavy, \(\delta_{jk}\) je Kroneckerovo delta a souřadnice polohového vektoru \(x_{(i)l}\) pro \(l=\) 1 až 3 jsou obecnějším zapsáním našich souřadnic \(x, \, y, \, z\) \(i\)-tého bodu.

  Poznámka: Odvození tohoto vztahu viz například: Studijní text k teoretické mechanice tuhého tělesa.

  V našem případě se vztah ještě zjednodušší, protože máme pouze 2 hmotné body.

  \[J_{jk}= m_{(1)} ( \delta_{jk} \, r_{(1)}^2 - x_{(1)j} \, x_{(1)k} ) + m_{(2)} ( \delta_{jk} \, r_{(2)}^2 - x_{(2)j} \, x_{(2)k} )\]

• Nápověda 2

  Určete jednotlivé složky tenzoru setrvačnosti a zapište je do matice.

• Řešení – Nápověda 2

  Začněme složkou \(J_{xx}\).

  \[J_{xx} = J_{11}= m_{(1)} ( \delta_{11} \, r_{(1)}^2 - x_{(1)}^2 ) + m_{(2)} ( \delta_{11} \, r_{(2)}^2 - x_{(2)}^2 ) = m_{(1)} ( \, y_{(1)}^2 + z_{(1)}^2 ) + m_{(2)} ( \, y_{(2)}^2 + z_{(2)}^2 )=\] \[= 2 M \, a^2 + M ( \, a^2 + a^2 ) = 4 M \, a^2\] \[J_{xx} = 4 M \, a^2\]

  Složku \(J_{yy}\) určíme velmi obdobně.

  \[J_{yy} = J_{22}= m_{(1)} ( \delta_{22} \, r_{(1)}^2 - y_{(1)}^2 ) + m_{(2)} ( \delta_{22} \, r_{(2)}^2 - y_{(2)}^2 ) = m_{(1)} ( \, x_{(1)}^2 + z_{(1)}^2 ) + m_{(2)} ( \, x_{(2)}^2 + z_{(2)}^2 )=\] \[= 2 M \, a^2 + M ( \, a^2 + a^2 ) = 4 M \, a^2\]

  Dále nám zbývá složka \(J_{zz}\).

  \[J_{zz} = J_{33}= m_{(1)} ( \delta_{33} \, r_{(1)}^2 - z_{(1)}^2 ) + m_{(2)} ( \delta_{33} \, r_{(2)}^2 - z_{(2)}^2 ) = m_{(1)} ( \, x_{(1)}^2 + y_{(1)}^2 ) + m_{(2)} ( \, x_{(2)}^2 + y_{(2)}^2 )=\] \[= 2 M ( \, a^2 + a^2 ) + M ( \, a^2 + a^2 ) = 6 M \, a^2\]

  Nyní je načase spočítat deviační momenty. Začněme složkou \(J_{xy}\).

  \[J_{xy} = J_{12}= m_{(1)} ( \delta_{12} \, r_{(1)}^2 - x_{(1)} y_{(1)} ) + m_{(2)} ( \delta_{12} \, r_{(2)}^2 - x_{(2)} y_{(2)} ) = - m_{(1)} x_{(1)} y_{(1)} - m_{(2)} x_{(2)} y_{(2)} =\] \[= - 2 M ( - a^2 ) - M a^2 = M \, a^2\]

  Budeme pokračovat určením \(J_{xz}\).

  \[J_{xz} = J_{13}= m_{(1)} ( \delta_{13} \, r_{(1)}^2 - x_{(1)} z_{(1)} ) + m_{(2)} ( \delta_{13} \, r_{(2)}^2 - x_{(2)} z_{(2)} ) = - m_{(1)} x_{(1)} z_{(1)} - m_{(2)} x_{(2)} z_{(2)} = - M a^2\]

  Vztah pro \(J_{yz}\) vyjde podobně.

  \[J_{yz} = J_{23}= m_{(1)} ( \delta_{23} \, r_{(1)}^2 - y_{(1)} z_{(1)} ) + m_{(2)} ( \delta_{23} \, r_{(2)}^2 - y_{(2)} z_{(2)} ) = - m_{(1)} y_{(1)} z_{(1)} - m_{(2)} y_{(2)} z_{(2)} = - M a^2\]

  Napišme celý tenzor setrvačnosti činky do matice.

  \[J = M a^2 \begin{pmatrix} 4 & 1 & -1 \\ 1 & 4 & -1\\ -1 & -1 & 6 \end{pmatrix}\]

• Nápověda 3

  Nyní budeme hledat vlastní vektory a vlastní čísla tenzoru setrvačnosti.

  Zavzpomínejte, jak se hledají vlastní vektory matice. Osvěžte si pojmy: vlastní čísla, vlastní vektor a charakteristický polynom.

• Řešení – Nápověda 3

  Mějme čtvercovou matici \(A\) nad \(\mathbb{R}\). Pak vlastním vektorem \(\vec {v}\) matice \(A\) rozumíme nenulový vektor, pro nějž platí, že

  \[A \vec v = \lambda \vec v ,\]

  kde \(\lambda \in \mathbb{R}\), \(\lambda\) je vlastní číslo matice \(A\) příslušné vlastnímu vektoru \(\vec v\).

  \[A \vec v - \lambda \vec v = \vec o\] \[\left( A - \lambda \mathbb{E} \right) \vec v = \vec o\]

  Matice \(\left( A - \lambda \mathbb{E} \right)\) je singulární, právě tehdy když má daná rovnice netriviální řešení, tedy musí platit:

  \[\mathrm{det} \left| A - \lambda \mathbb{E} \right| = 0.\]

  Tuto rovnici nazýváme charakterictickým polynomem a užíváme ji pro hledání vlastních čísel.

  Jakmile nalezneme vlastní čísla, užijeme rovnice \(\left( A - \lambda \mathbb{E} \right) \vec v = \vec o\) k nalezení vlastních vektorů matice \(A\).

• Nápověda 4

  Najděte vlastní čísla a vektory matice

  \[\begin{pmatrix} 4 & 1 & -1 \\ 1 & 4 & -1 \\ -1 & -1 & 6 \end{pmatrix} .\]

• Řešení – Nápověda 4

  Najděme kořeny charakteristického polynomu této matice.

  \[\mathrm{det} \left| A - \lambda \mathbb{E} \right| = \begin{vmatrix} 4 - \lambda & 1 & -1 \\ 1 & 4 - \lambda & -1 \\ -1 & -1 & 6 - \lambda \end{vmatrix} = \] \[= \left( 6 - \lambda \right) \left( 4 - \lambda \right)^2 +1 +1 - 2 \left( 4 - \lambda \right) - \left( 6 - \lambda \right)= \] \[= \left( 6 - \lambda \right) \left( 16 - 8 \lambda + \lambda^2 \right) + 2 + 2 \lambda - 8 - 6 + \lambda = \] \[= 96 -48 \lambda +6 \lambda^2 - 16 \lambda +8 \lambda^2 - \lambda^3 + 3 \lambda - 12=\] \[= - \lambda^3 + 14 \lambda^2 - 61 \lambda + 84 = 0\] \[\lambda^3 -14 \lambda^2 + 61 \lambda - 84 = 0\]

  Charakteristický polynom naší matice je kubická rovnice s nepříliš hezkými koeficienty. Takovouto rovnici lze řešit několika způsoby. Můžeme užít například Cardanovy vzorce, Hornerovo schéma nebo Vietovy vzorce. Užijeme posledního zmíněného. Jeden z Vietových vzorců říká, že:

  \[\lambda_1 \, \lambda_2 \, \lambda_3 = 84 = 2^2 {\cdot} 3 \cdot 7\]

  Zkusme tedy vzít třeba \(\lambda_1 = 7\), potom:

  \[\frac {\lambda^3 - 14 \lambda^2 + 61 \lambda - 84}{\lambda -7} = \lambda^2 - 7 \lambda + 12\]

  Platí tedy, že \(\lambda_1 = 7\) je kořenem charakteristického polynomu a dále proto stačí vyřešit kvadratickou rovnici ve tvaru:

  \[\lambda^2 - 7 \lambda + 12 = 0 .\] \[(\lambda - 4)(\lambda - 3) = 0\]

  Tedy už známe všechna vlastní čísla.

  \[\lambda_1 = 7 \, ; \, \lambda_2 = 4 \, ; \, \lambda_3 = 3\]

  Najděme vlastní vektor \(\vec {v_1}^T = (x_1 , \, y_1 , \, z_1 )\) příslušný vlastnímu číslu \(\lambda_1 = 7\).

  \[\left( A - \lambda_1 \mathbb{E} \right) \vec {v_1} = \begin{pmatrix} 4 - \lambda_1 & 1 & -1 \\ 1 & 4 - \lambda_1 & -1 \\ -1 & -1 & 6 - \lambda_1 \end{pmatrix} \vec {v_1} = \vec o\] \[\begin{pmatrix} -3 & 1 & -1 \\ 1 & -3 & -1 \\ -1 & -1 & -1 \end{pmatrix} \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} = \vec o\tag{1}\]

  Zjednodušme naši matici pro nalezení \(\vec {v_1}\).

  \[\begin{pmatrix} -3 & 1 & -1 \\ 1 & -3 & -1 \\ -1 & -1 & -1 \end{pmatrix} \sim \begin{pmatrix} -4 & 0 & -2 \\ 0 & 4 & 2 \\ 1 & 1 & 1 \end{pmatrix} \sim \begin{pmatrix} 2 & 0 & 1 \\ 0 & 2 & 1 \\ 1 & 1 & 1 \end{pmatrix} \sim \begin{pmatrix} 2 & 0 & 1 \\ 0 & 2 & 1 \\ 1 & -1 & 0 \end{pmatrix} \sim \begin{pmatrix} 2 & 0 & 1 \\ 2 & 0 & 1 \\ 1 & -1 & 0 \end{pmatrix}\]

  Vraťme se zpět k rovnici (1).

  \[\begin{pmatrix} 2 & 0 & 1 \\ 2 & 0 & 1 \\ 1 & -1 & 0 \end{pmatrix} \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} = \vec o\]

  Máme soustavu rovnic:

  \[\begin{matrix} 2 x_1 & & + z_1 & = 0 ; \\ x_1 & - y_1 & & = 0 . \end{matrix}\]

  Z druhé rovnice vidíme, že \(y_1 = x_1\) a z první, že \(x_1 = - \frac{1}{2} z_1\), a proto

  \[x_1 = y_1 = - \frac{1}{2} z_1 .\]

  Hledané řešení soustavy, je závislé na volbě jednoho parametru. Zvolme \(z_1 = - 2\). Potom pro vektor \(\vec {v_1}\) příslušný vlastnímu číslu \(\lambda_1 = 7\) platí:

  \[\vec {v_1}^T = (1 , \, 1 , \, -2 ) \, .\]

  Dále hledejme vlastní vektor \(\vec {v_2}^T = (x_2 , \, y_2 , \, z_2 )\) příslušný vlastnímu číslu \(\lambda_2 = 4\).

  \[\left( A - \lambda_2 \mathbb{E} \right) \vec {v_2} = \begin{pmatrix} 4 - \lambda_2 & 1 & -1 \\ 1 & 4 - \lambda_2 & -1 \\ -1 & -1 & 6 - \lambda_2 \end{pmatrix} \vec {v_2} = \vec o\] \[\begin{pmatrix} 0 & 1 & -1 \\ 1 & 0 & -1 \\ -1 & -1 & 2 \end{pmatrix} \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} = \vec o\tag{2}\]

  Opět si trochu poupravme naši matici.

  \[\begin{pmatrix} 0 & 1 & -1 \\ 1 & 0 & -1 \\ -1 & -1 & 2 \end{pmatrix} \sim \begin{pmatrix} 0 & 1 & -1 \\ 1 & 0 & -1 \\ 0 & -1 & 1 \end{pmatrix} \sim \begin{pmatrix} 0 & 1 & -1 \\ 1 & 0 & -1 \\ 0 & 0 & 0 \end{pmatrix}\]

  Tuto matici dosaďme do rovnice (2).

  \[\begin{pmatrix} 0 & 1 & -1 \\ 1 & 0 & -1 \\ 0 & 0 & 0 \end{pmatrix} \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} = \vec o\]

  Tím jsme dostali soustavu rovnic pro vektor \(\vec v_2\).

  \[\begin{matrix} & y_2 & - z_2 & = 0 ; \\ x_2 & & - z_2 & = 0 , \end{matrix}\]

  Z první rovnice plyne \(y_2 = z_2\) a z druhé plyne \(z_2 = x_2\).

  Opět vidíme, že máme volnost ve volbě parametru, pro jednoduchost vezměme \(x_2 = 1\). Pak tedy platí pro vektor \(\vec {v_2}\) příslušný vlastnímu číslu \(\lambda_2 = 4\):

  \[\vec {v_2}^T = (1 , \, 1 , \, 1 ) \, .\]

  Dále hledejme vlastní vektor \(\vec {v_3}^T = (x_3 , \, y_3 , \, z_3 )\) příslušný vlastnímu číslu \(\lambda_3 = 3\).

  \[\left( A - \lambda_3 \mathbb{E} \right) \vec {v_3} = \begin{pmatrix} 4 - \lambda_3 & 1 & -1 \\ 1 & 4 - \lambda_3 & -1 \\ -1 & -1 & 6 - \lambda_3 \end{pmatrix} \vec {v_3} = \vec o\] \[\begin{pmatrix} 1 & 1 & -1 \\ 1 & 1 & -1 \\ -1 & -1 & 3 \end{pmatrix} \begin{pmatrix} x_3 \\ y_3 \\ z_3 \end{pmatrix} = \vec o\tag{3}\]

  Matici si opět zjednodušíme.

  \[\begin{pmatrix} 1 & 1 & -1 \\ 1 & 1 & -1 \\ -1 & -1 & 3 \end{pmatrix} \sim \begin{pmatrix} 0 & 0 & 0 \\ 1 & 1 & -1 \\ 0 & 0 & 2 \end{pmatrix} \sim \begin{pmatrix} 0 & 0 & 0 \\ 1 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}\]

  Tuto matici dosaďme do rovnice (3).

  \[\begin{pmatrix} 0 & 0 & 0 \\ 1 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x_3 \\ y_3 \\ z_3 \end{pmatrix} = \vec o\]

  Opět máme soustavu rovnic, tentokrát pro vektor \(\vec v_3\).

  \[\begin{matrix} x_3 & + y_3 & & = 0 \\ & & z_3 & = 0 \end{matrix}\]

  Snadno nahlédneme, že \(x_3 = - y_3\). Volbou \(x_3 = 1\) určíme podobu vlastního vektoru \(\vec v_3\) příslušného vlastnímu číslu \(\lambda_3 = 3\).

  \[\vec {v_3}^T = (1 , \, -1 , \, 0 ) \, .\]

• Nápověda 5

  Přiřaďte výsledkům Nápovědy 4 fyzikální význam.

• Řešení – Nápověda 5

  Náš tenzor setrvačnosti činky měl tvar:

  \[J = M a^2 \begin{pmatrix} 4 & 1 & -1 \\ 1 & 4 & -1\\ -1 & -1 & 6 \end{pmatrix} = M a^2 A . \]

  Určená vlastní čísla \(\lambda_i\) jsou vlastní čísla matice \(A\). Proto získáme hlavní momenty setrvačnosti \(J_i\) prostým přepočtem \(J_i = \lambda_i \, M a^2\). Nalezené vlastní vektory \(\vec {v_i}\) odpovídají směrům hlavních os rotace s příslušnými hlavními momenty setrvačnosti \(J_i\).

  \[\begin{matrix} J_1 = 7 M a^2 & & \vec {v_1}^T = (1 , \, 1, \, -2 ) \\ J_2 = 4 M a^2 & & \vec {v_2}^T = (1 , \, 1 , \, 1 ) \\ J_3 = 3 M a^2 & & \vec {v_3}^T = (1 , \, -1 , \, 0 ) \end{matrix}\]

  Lze ověřit, že \(\vec {v_1}\) je kolmý na \(\vec {v_2}\) i \(\vec {v_3}\). Stejně tak \(\vec {v_2}\) je kolmý na \(\vec {v_3}\).

• Výpočet tenzoru setrvačnosti v nové bázi

  Námi určené hlavní momenty setrvačnosti \(J_i\) a k nim příslušné vlastní vektory \(\vec{v_i}\) jsou:

  \[\begin{matrix} J_1 = 7 M a^2 \, , & & \vec {v_1}^T = (1 , \, 1, \, -2 ) \, ; \\ J_2 = 4 M a^2 \, , & & \vec {v_2}^T = (1 , \, 1 , \, 1 ) \, ; \\ J_3 = 3 M a^2 \, , & & \vec {v_3}^T = (1 , \, -1 , \, 0 ) \, . \end{matrix}\]

  Podíváme-li se na zadání

  \[\begin{matrix} \vec{r_1} = \left( a; \, -a; \, 0 \right) , & & m_1 = 2 M ;\\ \vec{r_2} = \left( a; \, a; \, a \right) , & & m_2 = M , \end{matrix} \]

  domyslíme si, že vlastní vektor \(\vec {v_2}\) je lineárně závislý s vektorem \(\vec{r_2}\) a podobně je \(\vec {v_3}\) lineárně závislý s \(\vec{r_1}\).

  Pro opravdu názornou představu přikládám 3D náhled naší situace v online GeoGebře.

  Pokud bychom měli zapsat polohové vektory konců činky v nové bázi vlastních vektorů, označme je třeba čárkou jako \(\vec{r'_1}\) a \(\vec{r'_2}\), potom budou určitě ležet na nových souřadnicových osách. Abychom nemuseli normovat všechny vektory báze, určeme vzdálenost konců činky od počátku soustavy, tedy vlastně velikost \(\vec{r_1}\) a \(\vec{r_2}\):

  \[\left| \vec{r_1} \right| = \left| \left( a; \, -a; \, 0 \right) \right| = a \sqrt 2 \, ; \] \[\left| \vec{r_2} \right| = \left| \left( a; \, a; \, a \right) \right| = a \sqrt 3 \, .\]

  Vzhledem k naší nové ortonormální bázi pak budou souřadnice polohových vektorů:

  \[\vec{r'_1} = \left( 0; \, 0; \, a \sqrt 2 \right) \, ;\] \[\vec{r'_2} = \left( 0; \, a \sqrt 3; \, 0 \right) \, .\]

  Zkuste spočítat tenzor setrvačnosti činky vhledem k této bázi.

• Odpověď

  Tenzor setrvačnosti \(J\) naší činky vzhledem k počátku soustavy souřadnic je:

  \[J = M a^2 \begin{pmatrix} 4 & 1 & -1 \\ 1 & 4 & -1\\ -1 & -1 & 6 \end{pmatrix} .\]

  Hlavní momenty setrvačnosti \(J_i\) a jim příslušné hlavní osy rotace \(\vec {v_i}\) jsou:

  \[\begin{matrix} J_1 = 7 M a^2 \, , & & \vec {v_1}^T = (1 , \, 1, \, -2 ) \, ; \\ J_2 = 4 M a^2 \, , & & \vec {v_2}^T = (1 , \, 1 , \, 1 ) \, ; \\ J_3 = 3 M a^2 \, , & & \vec {v_3}^T = (1 , \, -1 , \, 0 ) \, . \end{matrix}\]