Malé kmity spřažených kyvadel různé hmotnosti
Úloha číslo: 2285
Mějme dvě matematická kyvadla různých hmotností \(m\) a \(M\) na tuhém závěsu délky \(l\). Kyvadla jsou zavěšena vedle sebe ve stejné výšce ve vzdálenosti \(d\). Kyvadla jsou spolu spojena pružinou tuhosti \(k\) o klidové délce \(d\).
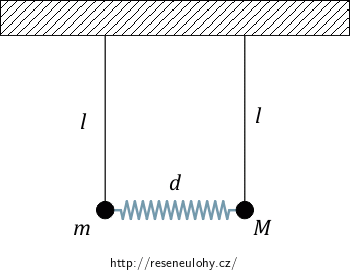
Určete pohybové rovnice pro tuto soustavu. Potenciální energii aproximujte pomocí teorie malých kmitů.
Nápověda 1
Zamyslete se, v jaké soustavě souřadnic bude výhodné náš problém popisovat.
Určete zobecněné souřadnice vhodné pro popis pohybu našich kyvadel.
Vyjádřete polohu a rychlost jednotlivých kyvadel.
Nápověda 2
Najděte lagrangián \(L\). Pro potenciální energii užijte aproximaci platnou pro malé kmity.
Nápověda 3
Užijte Lagrangeovy rovnice II. druhu
Celkové řešení
Zvolme soustavu souřadnic s počátkem v bodě zavěšení prvního kyvadla, jejíž osa \(x\) směřuje k bodu zavěšení druhého kyvadla a osa \(y\) je svislá.
Za zobecněné souřadnice budeme brát úhly \(\varphi_1\) a \(\varphi_2\) odklonu od svislého směru jednotlivých kyvadel tak, jak je zobrazeno na obrázku.
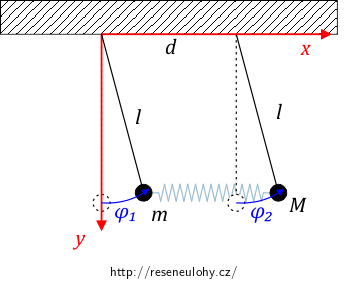
Pomocí goniometrických funkcí určíme souřadnice obou kyvadel.
\[\begin {matrix} x_1 = l \sin \varphi_1 & & & & x_2 = l \sin \varphi_2 + d \\ y_1 = l \cos \varphi_1 & & & & y_2 = l \cos \varphi_2 \end {matrix}\]Rychlosti kyvadel \(\vec v_1\) a \(\vec v_2\) již určíme snadno.
\[\vec v_1 = \left( l \cos \varphi_1 \cdot \dot \varphi_1 \, ; - l \sin \varphi_1 \cdot \dot \varphi_1 \right)\] \[\vec v_2 = \left( l \cos \varphi_2 \cdot \dot \varphi_2 \, ; - l \sin \varphi_2 \cdot \dot \varphi_2 \right)\]K určení lagrangiánu \(L = T - V\) budeme potřebovat znát vztahy pro kinetickou energii \(T\) a potenciální energii \(V\). Kinetickou energii určíme podle dobře známého vztahu \(T = \frac{1}{2} \sum_i m_i v_i^2\).
\[T = \frac{1}{2} m v_1^2 + \frac{1}{2} M v_2^2 = \] \[= \frac{1}{2} \left[ m l^2 \cos^2 \varphi_1 \cdot \dot \varphi_1^2 + m l^2 \sin^2 \varphi_1 \cdot \dot \varphi_1^2 + M l^2 \cos^2 \varphi_2 \cdot \dot \varphi_2^2 + M l^2 \sin^2 \varphi_2 \cdot \dot \varphi_2^2 \right]\] \[T = \frac{1}{2} l^2 \left( m \dot \varphi_1^2 + M \dot \varphi_2^2 \right)\]Do potenciální energie budeme muset zahrnout jak tíhovou potenciální energii \(V_t\), tak potenciální energii pružiny \(V_p\).
\[V = V_t + V_p\]Pro tíhovou potenciální energii \(V_p\)bude platit:
\[V_p = - m g y_1 - M g y_2 \, .\] \[V_p = - g l \left( m \cos \varphi_1 + M \cos \varphi_2 \right)\]Pro potenciální energii pružiny \(V_p\) platí:
\[V_p = \frac{1}{2} k \, \Delta d^2 \, ,\]kde \(\Delta d\) je prodloužení pružiny. V našem případě bude platit následující vztah.
\[V_p = \frac{1}{2} k \left( - l \sin \varphi_1 + l \sin \varphi_2 + d - d \right)^2\] \[V_p = \frac{k l^2}{2} \left( \sin \varphi_2 - \sin \varphi_1 \right)^2\]Tedy celková potenciální energie \(V\) bude mít tvar:
\[V = - g l \left( m \cos \varphi_1 + M \cos \varphi_2 \right) + \frac{k l^2}{2} \left( \sin \varphi_2 - \sin \varphi_1 \right)^2\]Jelikož nás zajímají pouze malé kmity v okolí rovnovážné polohy, budeme chtít potenciál aproximovat kvadratickou funkcí \(\varphi\).
Z Maclaurinových řad pro funkce \(\sin \varphi\) a \(\cos \varphi\) získáme hledanou aproximaci vcelku snadno.
\[\sin \varphi \approx \varphi\] \[\cos \varphi \approx 1 - \frac{\varphi^2}{2}\]Tedy se nám předpis pro potenciální energii \(V\) zjednodušší na:
\[V = - g l \left( m + M - \frac{ m \varphi_1^2 + M \varphi_2^2}{2} \right) + \frac{k l^2}{2} \left( \varphi_2 - \varphi_1 \right)^2 \, .\]A pro lagrangián \(L\) dostáváme:
\[L = \frac{1}{2} l^2 \left( m \dot \varphi_1^2 + M \dot \varphi_2^2 \right) + g l \left( m + M - \frac{ m \varphi_1^2 + M \varphi_2^2}{2} \right) - \frac{k l^2}{2} \left( \varphi_1 - \varphi_2 \right)^2 \, .\]Použijeme Lagrangeovy rovnice druhého druhu.
\[\frac{\partial}{\partial t} \left( \frac{\partial L}{\partial \dot{\varphi_i}} \right) - \frac{\partial L}{\partial \varphi_i} = 0\]Teď si spočítáme všechny potřebné derivace.
\[\frac{\partial L}{\partial \dot{\varphi_1}} = m l^2 \dot \varphi_1\] \[\frac{\partial L}{\partial \dot{\varphi_2}} = M l^2 \dot \varphi_2\] \[\frac{\partial L}{\partial \varphi_1} = - m g l \varphi_1 - k l^2 \left( \varphi_1 - \varphi_2 \right)\] \[\frac{\partial L}{\partial \varphi_2} = - M g l \varphi_2 + k l^2 \left( \varphi_1 - \varphi_2 \right)\]Nyní dosaďme do Lagrangeových rovnic a dostaneme pohybové rovnice pro jednotlivá kyvadla.
\[m l^2 \ddot \varphi_1 + m g l \varphi_1 + k l^2 \left( \varphi_1 - \varphi_2 \right) = 0\] \[M l^2 \ddot \varphi_2 + M g l \varphi_2 - k l^2 \left( \varphi_1 - \varphi_2 \right) = 0\]Přesně jak bychom očekávali, lze vidět, že pohyb jednoho kyvadla je skrze tuhost pružiny svázán s pohybem druhého.
\[\ddot \varphi_1 + \frac{g}{l} \varphi_1 + \frac{k}{m} \left( \varphi_1 - \varphi_2 \right) = 0\tag{1}\] \[\ddot \varphi_2 + \frac{g}{l} \varphi_2 - \frac{k}{M} \left( \varphi_1 - \varphi_2 \right) = 0\tag{2}\]Odpověď
Užijeme-li pro potenciální energii aproximace
\[V = - g l \left( m + M - \frac{m \varphi_1^2 + M \varphi_2^2}{2} \right) + \frac{k l^2}{2} \left( \varphi_2 - \varphi_1 \right)^2 \, ,\]budou mít pohybové rovnice pro naše kyvadla následující tvar.
\[\ddot \varphi_1 + \frac{g}{l} \varphi_1 + \frac{k}{m} \left( \varphi_1 - \varphi_2 \right) = 0\] \[\ddot \varphi_2 + \frac{g}{l} \varphi_2 - \frac{k}{M} \left( \varphi_1 - \varphi_2 \right) = 0\]

