Sbírka řešených úloh

Vozík na nakloněné rovině

Úloha číslo: 633

Po nakloněné rovině svírající s vodorovnou podložkou úhel α sjíždí vozík hmotnosti m. Poměr hmotnosti koleček a vozíku označme b, přičemž b může nabývat hodnot od 0 do 1 (tj. „počet procent bez vynásobení stem“). Kolečka považujeme za homogenní válce otáčející se kolem os procházejících středy jejich podstav.

Zanedbáme valivý odpor kol a tření v ložiscích.

Napište lagrangián pohybu vozíčku po nakloněné rovině a vyřešte Lagrangeovy rovnice II. druhu.

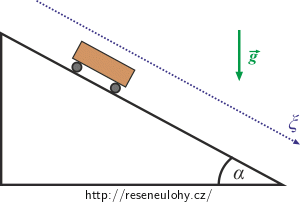
• Nápověda 1

  Musíme počítat s každým kolečkem zvlášť nebo nám jednoduše stačí uvažovat dvě části vozíku: „kolečka“ a „zbytek“? Prostudujte si úlohu Válec na nakloněné rovině.

• Řešení nápovědy 1

  K výpočtu lagrangiánu budeme potřebovat znát kinetickou energii koleček. Ta je však dána jen jejich celkovou hmotností a rychlostí pohybu (viz úloha Válec na nakloněné rovině). Odtud vidíme, že kinetická energie čtyř stejnou rychlostí se valících válců, resp. plných koleček je rovna:

  \[T = \frac{3}{4}m_1v^2 + \frac{3}{4}m_2v^2 + \frac{3}{4}m_3v^2 + \frac{3}{4}m_4v^2 = \frac{3}{4}(m_1 + m_2 + m_3 + m_4)v^2 = \frac{3}{4}m_{\mathrm{kolecka}}v^2,\]

  takže bude možné uvažovat kolečka „dohromady“.

  Problém není ani v tom, že jeden pár koleček je vzhledem ke sklonu roviny vždy výš, než druhý – je vzdálen jen o konstantu, tedy i potenciální energie se bude lišit pouze o konstantu, na níž pohybové rovnice nebudou záviset (viz rozbor v úloze Hmotný bod na nakloněné rovině).

• Nápověda 2

  Rozepište hmotnost částí „kolečka“ a „zbytek“ pomocí parametru b.

  Parametr b má význam procent hmotnosti. Pro praktické výpočty ho budeme používat v rozmezí od 0 do 1, tj. například 1 odpovídá 100%, tedy situaci, kdy můžeme hmotnost „zbytku vozíku“ oproti kolečkům zanedbat.

• Řešení nápovědy 2

  Celkovou hmotnost m rozepíšeme:

  \[m_{\mathrm{kolecka}} = bm\] \[m_{\mathrm{zbytek}} = (1-b)m\ ,\]

  tedy „co je hmotnosti v kolečcích, tolik musí ubýt ze zbytku“. Parametr b se pohybuje mezi 0 a 1. Je zřejmé, že platí:

  \[m = m_{\mathrm{kolecka}}+m_{\mathrm{zbytek}}\ .\]

• Nápověda 3

  Rozmyslete si, jaké pohyby konají kolečka a zbytek vozíku, a jak vyjádřit jejich kinetickou a potenciální energii.

• Řešení nápovědy 3

  Polohu těžiště vozíku popíšeme pomocí zobecněné souřadnice ξ, která míří podél povrchu nakloněné roviny dolů.

  Kolečka konají pohyb translační i rotační, zatímco zbytek pouze translační. Kinetickou energii zbytku tedy můžeme vzhledem k ní vyjádřit:

  \[T_{\mathrm{zbytek}}= \frac{1}{2}m_{\mathrm{zbytek}}\dot{\xi}^2 = \frac{1}{2}(1-b)m\dot{\xi}^2\ .\]

  Energii koleček rozepíšeme pomocí Königovy věty:

  \[T_{\mathrm{kolecka}} = \frac{1}{2}m_{\mathrm{kolecka}}v^2 + \frac{1}{2}J_{\mathrm{valec}}\omega^2\ .\]

  (detaily následujícího kroku viz úloha Válec na nakloněné rovině)

  \[T_{\mathrm{kolecka}}= \frac{3}{4}m_{\mathrm{kolecka}}\dot{\xi}^2 = \frac{3}{4}bm\dot{\xi}^2\ .\]

  Potenciální energie vozíku závisí jen na výšce těžiště, takže ji lze psát ve tvaru:

  \[V = -mg\xi \sin \alpha + V_0\ .\]

  V úloze Hmotný bod na nakloněné rovině jsme si ukázali, že konstantu V₀ můžeme bez újmy na obecnosti položit rovnu nule.

• Řešení – lagrangián

  Hmotnost jednotlivých částí jsme rozepsali pomocí parametru b.

  \[m_{\mathrm{kolecka}} = bm\] \[m_{\mathrm{zbytek}} = (b-1)m\]

  Pak jsme určili kinetickou energii jednotlivých částí:

  \[T_{\mathrm{zbytek}}= \frac{1}{2}(1-b)m\dot{\xi}^2\ .\] \[T_{\mathrm{kolecka}}= \frac{3}{4}bm\dot{\xi}^2\ .\]

  Potenciální energie vozíku je:

  \[V = -mg\xi \sin \alpha\ .\]

  Odtud lagrangián:

  \[L = \frac{1}{2}(1-b)m\dot{\xi}^2 + \frac{3}{4}bm\dot{\xi}^2 + mg\xi \sin \alpha =\] \[ = \frac{2+b}{4}m\dot{\xi}^2+ mg\xi \sin \alpha\ .\]

• Řešení – Lagrangeovy rovnice II. druhu a jejich řešení

  Z předchozího oddílu víme, že lagrangián má tvar:

  \[L = \frac{2+b}{4}m\dot{\xi}^2+ mg\xi \sin \alpha\ .\]

  Připravíme si jeho derivace:

  \[\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial L}{\partial \dot{\xi}} = \frac{2+b}{2}m\ddot{\xi}\ ,\] \[\frac{\partial L}{\partial \xi}= mg\sin\alpha\ ,\]

  Dostáváme Lagrangeovu rovnici II. druhu:

  \[\frac{2+b}{2}m\ddot{\xi} - mg\sin\alpha = 0\]

  a po jednoduchých úpravách:

  \[\ddot{\xi} = \frac{2}{2+b}g\sin\alpha\ .\]

  Rovnici dvakrát zintegrujeme:

  \[\xi(t) = \frac{1}{2+b}gt^2\sin\alpha + v_0t + \xi_0\ .\]

  kde v₀, resp. ξ₀ je rychlost, resp. poloha těžiště vozíku v čase t = 0.

  Jedná se tedy o rovnoměrně zrychlený pohyb se zrychlením \(\frac{1}{2+b}g\sin\alpha\).

• Odpověď

  Lagrangián vozíčku s kolečky představujícími b-procent hmotnosti celého vozíčku je:

  \[L = \frac{2+b}{4}m\dot{\xi}^2 + mg\xi \sin \alpha\]

  a jeho pohybová rovnice má tvar:

  \[\xi(t) = \frac{1}{2+b}gt^2\sin\alpha + v_0t + \xi_0\ .\]

  Jedná se tedy o rovnoměrně zrychlený pohyb se zrychlením \(\frac{1}{2+b}g\sin\alpha\). Čím větší část hmotnosti celého vozíku je v kolečcích, tj. čím větší b, tím pomaleji se po nakloněné rovině rozjíždí.

  Jednoduchou kontrolou správnosti nám může být, že pro

  • b = 0, tedy nehmotná kolečka, se jedná o lagrangián a pohybovou rovnici hmotného bodu na nakloněné rovině (viz Hmotný bod na nakloněné rovině).
  • b = 1, tj. všechna hmotnost vozíčku je v kolečcích, dostáváme lagrangián a pohybovou rovnici válce na nakloněné rovině (viz Válec na nakloněné rovině).

• Komentář

  Z rovnice je také zřejmé, že aproximace vozíčku jako hmotného bodu, zaujímají-li kolečka v porovnání se zbytkem konstrukce pouze jednotky procent celkové hmotnosti, je dobrá.

  Například pokud kolečka tvoří 10% celkové hmotnosti vozíku (b = 0,1), dostáváme pohybovou rovnici:

  \[\xi(t) = \frac{10}{21}gt^2\sin\alpha + v_0t + \xi_0\ .\]

  Pokud ji porovnáme s pohybovou rovnicí hmotného bodu na nakloněné rovině:

  \[\xi(t) = \frac{1}{2}gt^2\sin\alpha + v_0t + \xi_0\ ,\]

  vidíme, že chyba je velmi malá a pro většinu příkladů sloužících k ilustraci pohybu, nikoli pro popis přesných měření, prakticky zanedbatelná.