Rovnovážná poloha – různá řešení

Úloha číslo: 1187

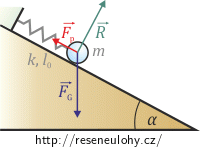
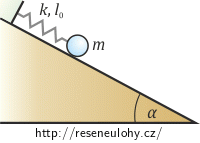
Hmotný bod o hmotnosti m je upevněn na pružině o tuhosti k a klidové délky l₀ a může se pohybovat po nakloněné rovině, která svírá s vodorovnou rovinou úhel α. Nalezněte jeho rovnovážnou polohu. Charakterizujte ji délkou pružiny l. Tření ani hmotnost pružiny neuvažujte.

Úlohu řešte:

pomocí silového diagramu (tj. prostředky mechaniky),
pomocí principu virtuální práce,
pomocí zobecněného principu virtuální práce v kartézských souřadnicích x, y dle obrázku,
pomocí zobecněného principu virtuální práce ve vhodné parametrizaci.

a) Nápověda 1
Rozmyslete si, které síly na hmotný bod působí. Nakreslete si obrázek a do něj tyto síly zaneste. Sestavte rovnici rovnováhy sil.
a) Řešení nápovědy 1
Na hmotný bod působí tři síly. Tíhová síla \(\vec{F}_G\) působící směrem k zemi, reakční síla \(\vec{R}\) působící kolmo k nakloněné rovině a síla pružnosti pružiny \(\vec{F}_p\), která působí ve směru nakloněné roviny.

Rovnice rovnováhy sil má tedy vektorový tvar:
\[\vec{F}_G+\vec{R}+\vec{F}_p=\vec{0}\]
a) Nápověda 2
Vhodně zvolte souřadnou soustavu, síly vyjádřete ve složkách a rozepište rovnici rovnováhy ve složkách.
a) Řešení nápovědy 2

Souřadnou soustavu jsme zvolili podle obrázku.

Síla \(\vec{F}_G\) má vzhledem k zavedení soustavy souřadnic tvar:
\[\vec{F}_G=(0;mg),\]
síla \(\vec{R}\) má vyjádření:
\[\vec{R}=(R\sin{\alpha};-R\cos{\alpha}),\]
kde α je úhel, který svírá nakloněná rovina s vodorovnou a R je velikost reakční síly.

Sílu \(\vec{F}_p\) vyjádříme pomocí aktuální délky pružiny l:
\[\vec{F}_p=(-k(l-l_0)\cos{\alpha};-k(l-l_0)\sin{\alpha}).\]
V souřadnicích tak získáváme dvě rovnice:
\[R\sin{\alpha}-k(l-l_0)\cos{\alpha}=0,\tag{1}\] \[mg-R\cos{\alpha}-k(l-l_0)\sin{\alpha}=0.\tag{2}\]
a) Nápověda 3
V předchozí nápovědě jsme získali soustavu dvou lineárních rovnic dvou neznámých, které popisují rovnovážný stav. Této soustavy využijte k vyjádření délky pružiny v rovnovážném stavu l.
a) Řešení nápovědy 3
Získali jsme soustavu dvou lineárních rovnic s nezmámými R (velikost reakční síly) a l (rovnovážná délka pružiny):
\[R\sin{\alpha}-k(l-l_0)\cos{\alpha}=0,\tag{1}\] \[mg-R\cos{\alpha}-k(l-l_0)\sin{\alpha}=0.\tag{2}\]
Z první rovnice vyjádříme R jako:
\[R=k(l-l_0)\frac{\cos{\alpha}}{\sin{\alpha}}\tag{3}\]
a dosadíme do druhé rovnice. Dostáváme:
\[mg-k(l-l_0)\frac{\cos^2{\alpha}}{\sin{\alpha}}-k(l-l_0)\sin{\alpha}=0.\]
Z druhého a třetího členu vytkneme \(k(l-l_0)\):
\[mg-k(l-l_0)\frac{\cos^2{\alpha}+\sin^2{\alpha}}{\sin{\alpha}}=0.\]
S využitím součtového vzorce \(\cos^2{\alpha}+\sin^2{\alpha}=1\) upravíme rovnici do tvaru:
\[k(l-l_0)\frac{1}{\sin{\alpha}}=mg\]
a vyjádříme hledanou délku l:
\[l=\frac{mg\sin{\alpha}}{k}+l_0.\]
Ze silového diagramu můžeme vidět, že reakční síla \(\vec{R}\) je kompenzována složkou tíhové síly \(\vec{F}_G\) do jejího směru. Velikost reakční síly R získáme dosazením za l do vztahu (3):
\[R=k\frac{mg\sin{\alpha}}{k}\frac{\cos{\alpha}}{\sin{\alpha}}=mg\cos{\alpha}.\]
Výsledek odpovídá právě průmětu tíhové síly \(\vec{F}_G\) do směru kolmého na nakloněnou rovinu.

Proberme si ještě speciální případy.

Pokud by byl úhel α = 0°, tedy pružina s hmotným bodem by se nacházela na vodorovné rovině, zjednodušila by se podmínka rovnováhy na:
\[l=l_0.\]
V případě, že by naopak úhel α = 90°, což odpovídá hmotnému bodu volně visícímu na pružině, redukovala by se podmínka rovnováhy do tvaru:
\[l=\frac{mg}{k}+l_0.\]
Oba případy dobře odpovídají naší představě.
b) Nápověda 1
Napište princip virtuální práce a dosaďte do něj.
b) Řešení nápovědy 1
Princip virtuální práce zní takto:
\[\sum_{i=1}^N \vec{F_i}\cdot\delta\vec{r_i}=0,\]
kde \(\vec{F_i}\) jsou výslednice všech sil na i-tý hmotný bod a \(\vec{r_i}\) jsou všechna virtuální posunutí i-tého hmotného bodu.

Po dosazení vyjádření sil nabývá princip virtuální práce v našem případě podoby (složky jednotlivých sil naleznete vypsané v oddíle a):
\[(R\sin{\alpha}-k(l-l_0)\cos{\alpha})\delta x+ (mg-R\cos{\alpha}-k(l-l_0)\sin{\alpha})\delta y=0.\]
b) Nápověda 2
Rovnice z minulé nápovědy musí platit pro všechna virtuální posunutí. Zkuste zvolit speciální případy δx a δy a získat tak dvě jednodušší rovnice.
b) Řešení nápovědy 2
Dosazením do principu virtuální práce jsme získali rovnici:
\[(R\sin{\alpha}-k(l-l_0)\cos{\alpha})\delta x+ (mg-R\cos{\alpha}-k(l-l_0)\sin{\alpha})\delta y=0.\]
Tato rovnice musí platit pro libovolná virtuální posunutí, tedy i pro δx ≠ 0 a δy = 0. V takovém případě dospějeme k rovnici:
\[R\sin{\alpha}-k(l-l_0)\cos{\alpha}=0.\]
Naopak pro případ δx = 0 a δy ≠ 0 dostáváme:
\[mg-R\cos{\alpha}-k(l-l_0)\sin{\alpha}=0.\]
Tyto dvě rovnice jsou již shodné s rovicemi (1) a (2) z nápovědy 2 části a). Dále již může řešení pokračovat stejnými kroky jako v části a) a dospět ke stejnému výsledku.
c) Nápověda 1
Napište zobecněný princip virtuální práce a dosaďte do něj.
c) Řešení nápovědy 1
Zobecněný princip virtuální práce zní takto:
\[\sum_{i=1}^N \vec{F^{(a)}_i}\cdot\delta\vec{r_i}=0,\]
kde \(\vec{F^{(a)}_i}\) jsou výslednice vtištěných sil (vtištěným silám se také říká aktivní síly, proto index a) na i-tý hmotný bod a \(\vec{r_i}\) jsou vratná virtuální posunutí slučitelná s vazbami i-tého hmotného bodu.

Uvažujeme pouze vtištěné síly, tedy reakci \(\vec{R}\) podložky, jež je silou vazbovou, uvažovat nebudeme. Dosadíme tedy do zobecněného principu virtuální práce (složky jednotlivých sil naleznete vypsané v oddíle a):
\[-k(l-l_0)\cos{\alpha}\delta x+ (mg-k(l-l_0)\sin{\alpha})\delta y=0.\]
c) Nápověda 2
Má-li být virtuální posunutí vratné a slučitelné s vazbami, potom jeho složky δx a δy na sobě nejsou nezávislé. Musí splňovat vazbovou podmínku (tak, aby hmotný bod zůstal na nakloněné rovině i po posunutí). Využijte vazbové podmínky k nalezení vztahu mezi oběma složkami virtuálního posunutí.
c) Řešení nápovědy 2
Vazbovou podmínku setrvání hmotného bodu na nakloněné rovině vyjádříme jako:
\[y=x\,\mathrm{tg}\,\alpha.\]
Přesvědčíte se o tom při pohledu na obrázek v oddíle a) Řešení nápovědy 2.

Pro složky virtuálního posunutí dostáváme derivováním:
\[\delta y=\mathrm{tg}\,\alpha\,\delta x.\]
Dosazením za δy z předchozího vztahu tak dostáváme rovnici:
\[-k(l-l_0)\cos{\alpha}\,\delta x+ (mg-k(l-l_0)\sin{\alpha})\mathrm{tg}\,\alpha\,\delta x=0.\]
Jelikož rovnice musí platit pro libovolnou hodnotu \(\delta x\), můžeme ji vydělit \(\delta x\) a upravit do tvaru:
\[k(l-l_0)\frac{\cos^2{\alpha}+\sin^2{\alpha}}{\cos{\alpha}}=mg\frac{\sin{\alpha}}{\cos{\alpha}}.\]
Délku l pak vyjádříme jako:
\[l=\frac{mg\sin{\alpha}}{k}+l_0.\]
Dostali jsme stejný výsledek jako v předchozích oddílech.
d) Nápověda 1
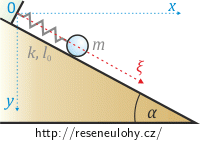
Úlohu máme řešit pomocí zobecněného principu virtuální práce při vhodné parametrizaci. Proto je třeba zvolit parametr, na který nebudou kladeny žádné podmínky související s vazbami, které omezují pohyb hmotného bodu. Vhodným parametrem je vzdálenost ξ od počátku soustavy souřadnic.
d) Řešení nápovědy 1

Jako parametr jsme zvolili vzdálenost ξ od počátku soustavy souřadnic. Na tento parametr neklademe žádnou podmínku. Parametr tak může nabývat libovolné hodnoty. Vyjádříme pomocí něho souřadnice x a y:
\[x=\xi\cos{\alpha},\] \[y=\xi\sin{\alpha}.\]
Z toho pro virtuální posunutí derivováním získáme:
\[\delta x=\cos{\alpha}\delta\xi,\] \[\delta y=\sin{\alpha}\delta\xi.\]
Napíšeme rovnici zobecněného principu práce tak, jak jsme ji získali v části c:
\[-k(l-l_0)\cos{\alpha}\delta x+ (mg-k(l-l_0)\sin{\alpha})\delta y=0\]
a dosadíme za virtuální posunutí δx a δy:
\[-k(l-l_0)\cos{\alpha}\cos{\alpha}\delta\xi+ (mg-k(l-l_0)\sin{\alpha})\sin{\alpha}\delta\xi=0.\]
Jelikož rovnice musí platit pro libovolnou hodnotu posunutí \(\delta\xi\), můžeme ji vydělit \(\delta\xi\) a upravit do tvaru:
\[k(l-l_0)(\cos^2{\alpha}+\sin^2{\alpha})=mg\sin{\alpha}.\]
Délku l tedy můžeme vyjádřit ve tvaru:
\[l=\frac{mg\sin{\alpha}}{k}+l_0.\]
Opět jsme získali stejné řešení jako v předchozích oddílech.
Celkové řešení
V celkovém řešení se nejprve zaměříme na zadání a).

Na hmotný bod působí tři síly. Tíhová síla \(\vec{F}_G\) působící směrem k zemi, reakční síla \(\vec{R}\) působící kolmo k nakloněné rovině a síla pružnosti pružiny \(\vec{F}_p\), která působí ve směru nakloněné roviny.

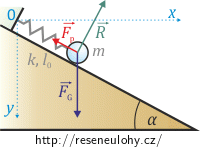
Rovnice rovnováhy sil má tedy vzhledem ke zvolené soustavě souřadné vektorový tvar:
\[\vec{F}_G+\vec{R}+\vec{F}_p=\vec{0}.\]
Vzhledem k zavedení souřadnic mají síly vyjádření po složkách:
\[\vec{F}_G=(0;mg),\] \[\vec{R}=(R\sin{\alpha};-R\cos{\alpha}),\] \[\vec{F}_p=(-k(l-l_0)\cos{\alpha};-k(l-l_0)\sin{\alpha}).\]
Vektorovou rovnici tak můžeme rozepsat po složkách a získáme tak soustavu dvou rovnic:
\[R\sin{\alpha}-k(l-l_0)\cos{\alpha}=0,\tag{1}\] \[mg-R\cos{\alpha}-k(l-l_0)\sin{\alpha}=0.\tag{2}\]
Řešením této soustavy (podrobně viz nápověda 3) dostaneme podmínku rovnováhy hmotného bodu, která je určena délkou pružiny l:
\[l=\frac{mg\sin{\alpha}}{k}+l_0.\]
V oddílu b) řešíme úlohu pomocí principu virtuální práce:

Princip virtuální práce zní takto:
\[\sum_{i=1}^N \vec{F_i}\cdot\delta\vec{r_i}=0,\]
kde \(\vec{F_i}\) jsou výslednice všech sil na i-tý hmotný bod a \(\vec{r_i}\) jsou všechna virtuální posunutí i-tého hmotného bodu.

Po dosazení vyjádření sil nabývá princip virtuální práce v našem případě podobu:
\[(R\sin{\alpha}-k(l-l_0)\cos{\alpha})\delta x+ (mg-R\cos{\alpha}-k(l-l_0)\sin{\alpha})\delta y=0.\]
Tato rovnice musí platit pro libovolná virtuální posunutí, tedy i pro δx ≠ 0 a δy = 0. V takovém případě dospějeme k rovnici:
\[R\sin{\alpha}-k(l-l_0)\cos{\alpha}=0.\]
Naopak pro případ δx = 0 a δy ≠ 0 dostáváme:
\[mg-R\cos{\alpha}-k(l-l_0)\sin{\alpha}=0.\]
Tyto dvě rovnice jsou již shodné s rovicemi (1) a (2) z nápovědy 2 části a). Dále již může řešení pokračovat stejnými kroky jako v části a) a dospět ke stejnému výsledku.

V části c) řešíme úlohu pomocí zobecněného principu virtuální práce, který má znění:
\[\sum_{i=1}^N \vec{F^{(a)}_i}\cdot\delta\vec{r_i}=0,\]
kde \(\vec{F^{(a)}_i}\) jsou výslednice vtištěných sil (vtištěným silám se také říká aktivní síly, proto index a) na i-tý hmotný bod a \(\vec{r_i}\) jsou vratná virtuální posunutí slučitelná s vazbami i-tého hmotného bodu.

Uvažujeme pouze vtištěné síly, tedy reakci \(\vec{R}\) podložky, jež je silou vazbovou, uvažovat nebudeme. Dosadíme tedy do zobecněného principu virtuální práce:
\[-k(l-l_0)\cos{\alpha}\delta x+ (mg-k(l-l_0)\sin{\alpha})\delta y=0.\]
Pohyb hmotného bodu musí zároveň splňovat vazbovou podmínku pro setrvání na nakloněné rovině:
\[y=x\,\mathrm{tg}\,\alpha\]
a tedy pro složky virtuálního posunutí dostáváme derivováním:
\[\delta y=\mathrm{tg}\,\alpha\,\delta x.\]
Dosazením za δy tak dostáváme rovnici:
\[-k(l-l_0)\cos{\alpha}\,\delta x+ (mg-k(l-l_0)\sin{\alpha})\mathrm{tg}\,\alpha\,\delta x=0.\]
Jelikož rovnice musí platit pro libovolnou hodnotu \(\delta x\), můžeme ji vydělit \(\delta x\) a upravit do tvaru:
\[k(l-l_0)\frac{\cos^2{\alpha}+\sin^2{\alpha}}{\cos{\alpha}}=mg\frac{\sin{\alpha}}{\cos{\alpha}}.\]
Délku l pak vyjádříme jako:
\[l=\frac{mg\sin{\alpha}}{k}+l_0.\]
V oddílu d) řešíme úlohu pomocí zobecněného principu virtuální práce při vhodné parametrizaci.

Jako nezávislý parametr zvolíme vzdálenost ξ od počátku soustavy souřadnic. Vyjádříme pomocí něho souřadnice x a y:
\[x=\xi\cos{\alpha},\] \[y=\xi\sin{\alpha}.\]
Z toho pro virtuální posunutí derivováním získáme:
\[\delta x=\cos{\alpha}\delta\xi,\] \[\delta y=\sin{\alpha}\delta\xi.\]
Napíšeme rovnici zobecněného principu práce tak, jak jsme ji získali v části c):
\[-k(l-l_0)\cos{\alpha}\delta x+ (mg-k(l-l_0)\sin{\alpha})\delta y=0\]
a dosadíme za virtuální posunutí δx a δy:
\[-k(l-l_0)\cos{\alpha}\cos{\alpha}\delta\xi+ (mg-k(l-l_0)\sin{\alpha})\sin{\alpha}\delta\xi=0.\]
Jelikož rovnice musí platit pro libovolnou hodnotu posunutí \(\delta\xi\), můžeme ji vydělit \(\delta\xi\) a upravit do tvaru:
\[k(l-l_0)(\cos^2{\alpha}+\sin^2{\alpha})=mg\sin{\alpha}.\]
Délku l tedy můžeme vyjádřit ve tvaru:
\[l=\frac{mg\sin{\alpha}}{k}+l_0.\]