Rovnovážná poloha závaží na dvouramenném mechanismu s pružinou
Úloha číslo: 2170
Mechanismus na obrázku se skládá ze dvou tuhých tyček a pružiny. V místě A je pevně upevněn ke stěně, bod \(C\) se může volně pohybovat. Pružina propojující body A a C má tuhost \(k\) a klidovou délku \(l_0\). Každá z tuhých tyček má délku \(a\). Pomocí principu virtuální práce najděte vztah pro rovnovážnou polohu mechanismu (vyjádřený pomocí úhlu \(\vartheta\)), pokud v místě B působíme na mechanismus silou o velikosti \(\vec{F}\) směrem dolů. Hmotnost celého mechanismu zanedbejte.
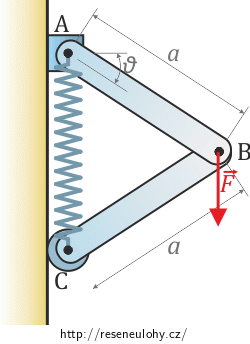
Nápověda 1
Rozmyslete si, jaké všechny aktivní síly v soustavě působí (užijeme zobecněný princip virtuální práce, vazbovými silami se zde nebudeme zabývat) a zakreslete je do obrázku. Zvolte si vhodnou soustavu souřadnic.
Nápověda 2
Určete souřadnice bodů \(A, \, B\) a \(C\) a složky sil vzhledem k naší soustavě souřadnic.
Nápověda 3
Určete virtuální posunutí.
Kompletní řešení
Soustavu souřadnic jsme zvolili s počátkem v bodě A, osa \(x\) směřuje ve vodorovném směru od stěny a osa \(y\) svisle dolů podél stěny.
Sílu pružnosti působící na bod A označme \(\vec {F_A}\), na bod \(C\) \(\vec {F_C}\).
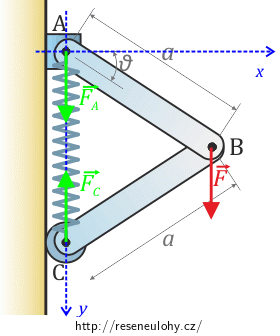
Nyní vyjádřeme polohu bodů a složky sil pomocí úhlu \(\vartheta\).
Užitím goniometrických vztahů dostaneme pro polohy bodů tyto souřadnice:
A: \([0;\, 0]\);
B: \([a \cos{\vartheta};\, a \sin{\vartheta}]\);
C: \([0;\, 2a \sin{\vartheta}]\).
Pro vyjádření sil je nutné užít vztahu pro výpočet síly pružnosti, tedy, že to je tuhost pružiny vynásobená prodloužením a znaménko je závislé na orientaci vůči námi zvolené soustavě souřadnic. S touto znalostí získáme:
\[\vec {F_A}:\, \left( 0;\,k(2a \sin{\vartheta}-l_0)\, \right);\] \[\vec {F_B}:\, \left( 0;\, F \right);\] \[\vec {F_C}:\, \left( 0;\, -k(2a \sin{\vartheta}-l_0)\, \right).\]Dále určíme daná virtuální posunutí, jež mohou být i nekonečně malá a chovají se podobně jako diferenciály. Úhel \(\vartheta\) považujme za zobecněnou souřadnici a naše virtuální posunutí \(\delta \vec{r_i}\) lze tedy určit jako:
\[\delta \vec{r_A}: \, \left( 0;\, 0 \right);\] \[\delta \vec{r_B}: \, \left( -a \sin{\vartheta} \, \delta \vartheta;\, a \cos{\vartheta} \, \delta \vartheta \right);\] \[\delta \vec{r_C}: \, \left( 0;\, 2a \cos{\vartheta} \, \delta \vartheta \right).\]Víme, že v rovnovážné poloze platí, že výslednice všech sil působících na těleso je nulová. Z této podmínky vychází princip virtuální práce, jež užijeme k řešení úlohy. Zobecněný princip virtuální práce (ZPVP) pro soustavu \(N\) hmotných bodů říká, že pro libovolná vratná virtuální posunutí slučitelná s vazbami \(\delta \vec {r_i}\) platí, že virtuální práce aktivních sil \(\vec {F_i^{(a)}}\) působících na soustavu pro tato virtuální posunutí je nulová, tedy:
\[\delta W=\sum_{i=1}^N {\vec {F_i^{(a)}} \cdot \delta \vec {r_i}}=0.\]V našem případě dostaneme rovnici:
\[\vec{F_A} \cdot \delta \vec{r_A} + \vec{F_B} \cdot \delta \vec{r_B} + \vec{F_C} \cdot \delta \vec{r_C} = 0.\]Což po skalárním vynásobení a dosazení dá:
\[0 {\cdot} 0 \, \delta\vartheta + 0 \cdot k(2a \sin{\vartheta}-l_0) \, \delta \vartheta -\] \[-0 \cdot a \sin{\vartheta} \, \delta\vartheta + F \cdot a \cos{\vartheta} \, \delta \vartheta +\] \[0 {\cdot} 0 \, \delta\vartheta - 2a \cos{\vartheta} \cdot k(2a \sin{\vartheta}-l_0) \, \delta \vartheta = 0.\]Upravíme na:
\[F a \cos{\vartheta} \, \delta \vartheta - 2a \cos{\vartheta} k(2a \sin{\vartheta}-l_0) \, \delta \vartheta = 0.\]Dále uvažujme, že \(\cos{\vartheta} \neq 0\), neboť pro \(\cos{\vartheta} = 0 \, \Rightarrow \,\vartheta = \frac {\pi}{2}\), což by ovšem znamenalo, že se náš stroj celý narovnal do směru osy \(y\). Tento případ nebudeme prozatím uvažovat a můžeme tedy rovnici pokrátit celým výrazem \(a \cos{\vartheta}\).
\[F a \cos{\vartheta} \, \delta \vartheta - 2a \cos{\vartheta} k(2a \sin{\vartheta}-l_0) \, \delta \vartheta = 0 \,\,\,\,\,\,\,\,\, / \frac{1}{a \cos{\vartheta}}\] \[\left[ F - 2k(2a \sin{\vartheta}-l_0) \right] \, \delta \vartheta = 0\]Ovšem tato rovnice musí platit pro zcela libovolná virtuální posunutí slučitelná s vazbami, tedy i nenulová posunutí, z čehož plyne, že výraz v hranaté závorce musí být roven nule.
\[F - 2k(2a \sin{\vartheta}-l_0)=0\] \[\frac{F}{2k}+l_0=2a \sin{\vartheta}\] \[\frac{F}{4ka}+\frac{l_0}{2a}= \sin{\vartheta}\] \[\frac{F+2k l_0}{4ka}= \sin{\vartheta}\]Pro náš úhel \(\vartheta\), který přesně určuje rovnovážnou polohu soustavy platí:
\[\vartheta = \arcsin{\left( \frac{F+2k l_0}{4ka} \right) }. \]Ověření
(A) Udělejmě rozměrovou zkoušku.
Argument funkce \(\arcsin\) by měl být bezrozměrný. Výraz \(2k l_0\) je tuhost pružiny násobená nějakou vzdáleností, tedy má rozměr síly, stejně tak výraz \(4ka\), tedy celý podíl \(\frac{F+2k l_0}{4ka}\) je bezrozměrný.(B) Jaký bude úhel \(\vartheta\) když nebudeme silou \(\vec F\) působit? (\(\vec F = \vec 0\))
\[\sin \vartheta = \frac{2k l_0}{4ka} = \frac {\frac {l_0}{2}}{a}\tag{1}\]To že síla \(\vec F\) je nulová odpovídá situaci, kdy má pružina klidovou délku. Vztah (1) odkoukáme z trojúhelníku \(\mathrm{ABS_{AC}}\).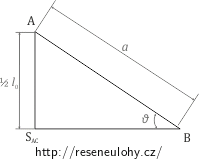
(C) Kdy dojde k úplnému napnutí mechanismu?
Funkce \(\arcsin\) je rostoucí, tedy pro rostoucí \(F\) bude růst i náš úhel \(\vartheta\), což je chování, jaké bychom očekávali - když budeme na bod \(B\) zvětšovat sílu, bude se bod \(B\) posouvat dolů, až dospějeme do místa, kde \(\vartheta = \frac {\pi}{2}\).\[ \sin \vartheta = \sin \frac {\pi}{2} = 1 = \frac{F + 2k l_0}{4ka}\] \[4ka - 2k l_0 = F\] \[2k (2a - l_0) = F\tag{2}\]To je ovšem vztah pro dvojnásobek síly pružnosti při natažení na délku \(2a\). Proč dvojnásobek? Pružina je na našem mechanismu napínána ve dvou bodech - \(A\) a \(C\). Síla \(\vec F\) tedy musí překonávat dvojnásobek síly pružnosti. Ve vztahu (2) dostáváme, že pro síly větší než je tato mez, je mechanismus plně natažen ve směru osy \(y\).Odpověď
Pro námi hledaný úhel \(\vartheta\), který přesně určuje rovnovážnou polohu soustavy platí:
\[\vartheta = \arcsin{\left( \frac{F+2k l_0}{4ka} \right)}.\]

