Sbírka řešených úloh

Kubická rovnice III.

Úloha číslo: 1611

• Teorie: Goniometrické řešení casus irreducibilis

  Stojíme-li před kubickou rovnicí typu casus irreducibilis, lze kořeny nalézt goniometricky, jak ukazuje následující věta.

  (i) O casu irreducibilis (nezjednodušitelném případu)

  Je-li diskriminant kubické rovnice v redukovaném tvaru \(x^3 + px + q = 0\) záporný (tj. jde o casus irreducibilis), pak kořeny najdeme tak, že nalezneme \(\alpha\in(0,\pi)\) splňující rovnici \[ \cos 3\alpha = -\frac{q}{2}\sqrt{-\frac{27}{q^3}} \] a toto \(\alpha\) pak užijeme k výpočtu kořenů \[ \begin{eqnarray} x_1 &=& 2\sqrt{-\frac{p}{3}}\cos\alpha, \\ x_2 &=& 2\sqrt{-\frac{p}{3}}\cos\left(\alpha + \frac{2\pi}{3}\right), \\ x_3 &=& 2\sqrt{-\frac{p}{3}}\cos\left(\alpha + \frac{4\pi}{3}\right). \\ \end{eqnarray} \]

  Jak poznáme, že se jedná o casus irreducibilis, jsme řešili v úloze Počty reálných kořenů kubické rovnice.

• Nápověda 1 – typ kubické rovnice

  Určete o jakou kubickou rovnici se jedná, tj. určete počet a typ kořenů. Nápovědou může být rozbor provedený v úloze Počty reálných kořenů kubické rovnice.

• Řešení nápovědy 1 – typ kubické rovnice

  Pro zadanou rovnici je \[p = -19, \qquad q = -30,\] tj. diskriminant \[ D = \left(\frac{-30}{2}\right)^2 + \left(\frac{-19}{3}\right)^3 \lt 0. \]

  Diskriminant je záporný, ze závěrů příkladu Počty reálných kořenů kubické rovnice vyplývá, že se jedná o casus irreducibilis. Rovnice má tedy tři různé reálné kořeny

• Nápověda 2 – hledání kořenů

  Casus irreducibilis je případ, kdy má kubická rovnice tři reálné kořeny, ale při užití Cardanových vzorců dostaneme obecně nezjednodušitelný součet třetích odmocnin komplexních čísel. Proveďte tedy goniometrický výpočet.

• Řešení nápovědy 2 – hledání kořenů

  Budeme postupovat podle zmíněné věty. Nejprve vypočítáme \(\alpha \in (0,\pi)\) z \[ \cos 3\alpha = -\frac{q}{2}\sqrt{-\frac{27}{q^3}}. \] Po vyjádření a dosazení \[ \alpha = \frac{1}{3} \arccos \left(15\sqrt{\frac{27}{19^3}}\right). \] Toto \(\alpha\) uložíme do paměti a použijeme k výpočtu kořenů \[ \begin{eqnarray} x_1 &=& 2\sqrt{\frac{19}{3}}\cos\alpha = 5, \\ x_2 &=& 2\sqrt{\frac{19}{3}}\cos\left(\alpha + \frac{2\pi}{3}\right) = -3, \\ x_3 &=& 2\sqrt{\frac{19}{3}}\cos\left(\alpha + \frac{4\pi}{3}\right) = -2. \\ \end{eqnarray} \] Kalkulačku je nutno přepnout „do radiánů“ nebo příslušné části argumentu přepočítat do stupňové míry.

  Rovnice má tři reálné kořeny

  \[x_1 =5,\qquad x_2=-3,\qquad x_3=-2.\] Můžeme ještě kořeny zakreslit jako nulové body grafu příslušné kubické funkce.

  

• Odpověď

  Kubická rovnice

  \[x^3 - 19x - 30 = 0\]

  má tři různé reálné kořeny (casus irreducibilis)

  \[x_1 =5,\qquad x_2=-3,\qquad x_3=-2,\]

  Tyto kořeny jsme jsme určili goniometricky.

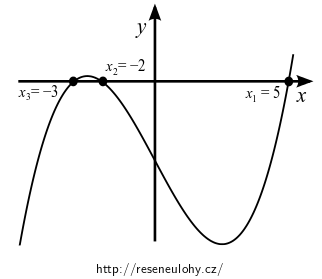
  Kořeny jako nulové body grafu příslušné kubické funkce: