Sbírka řešených úloh

Kubická rovnice II.

Úloha číslo: 1610

• Teorie

  Před řešením úlohy je dobré mít propočítané tyto příklady:

  • Cardanovy vzorce,
  • Počty reálných kořenů kubické rovnice,
  • Kubická rovnice I.

• Nápověda 1 – převedení do redukovaného tvaru

  Vhodnou substitucí převeďte rovnici do redukovaného tvaru, tj. „zbavte“ se kvadratického členu.

• Řešení nápovědy 1 – převedení do redukovaného tvaru

  Řešíme rovnici

  \[ x^\color{maroon}{3} \color{blue}{+3}x^2 - 54 = 0. \]

  Proveďme substituci \(x = y - \frac{\color{blue}{3}}{\color{maroon}{3}}\), tj. \(x=y-1\). Její mocniny

  \[ \begin{eqnarray} x &=& y-1, \\ x^2 &=& y^2 - 2y + 1, \\ x^3 &=& y^3 - 3y^2 + 3y - 1, \end{eqnarray} \]

  dosadíme

  \[ y^3 \color{red}{- 3y^2} + 3y - 1 \color{red}{+ 3y^2} - 6y + 3 - 54 = 0, \]

  čímž dostaneme kubickou rovnici bez kvadratického členu

  \[ y^3 - 3y - 52 = 0, \]

  jejíž řešení budeme hledat pomocí Cardanových vzorců.

• Nápověda 2 – hledání kořenů

  Pomocí Cardanových vzorců nalezněte řešení redukované kubické rovnice.

  Cardanovy vzorce:

  \[ \begin{eqnarray} y_1 &=& u + v, \\ y_2 &=& \varepsilon u + \varepsilon^2 v, \\ y_3 &=& \varepsilon^2 u + \varepsilon v, \end{eqnarray} \] \[\small\text{kde }\quad u = \sqrt[3]{-\frac{q}{2} + \sqrt{\left(\frac{q}{2}\right)^2 + \left(\frac{p}{3}\right)^3}}, \qquad v = \sqrt[3]{-\frac{q}{2} - \sqrt{\left(\frac{q}{2}\right)^2 + \left(\frac{p}{3}\right)^3}},\] \[ \text{a }\quad\small\varepsilon = -\frac{1}{2}+\frac{\sqrt{3}}{2} i. \]

• Řešení nápovědy 2 – hledání kořenů

  Řešíme redukovanou kubickou rovnici

  \[ y^3 - 3y - 52 = 0, \]

  tj. do Cardanových vzorců dosadíme \(p=-3\) a \(q=-52\)

  \[ u = \sqrt[3]{-\frac{-52}{2} + \sqrt{\left(\frac{-52}{2}\right)^2 + \left(\frac{-3}{3}\right)^3}} = \sqrt[3]{26 + 15\sqrt{3}}, \] \[ v = \sqrt[3]{-\frac{-52}{2} - \sqrt{\left(\frac{-52}{2}\right)^2 + \left(\frac{-3}{3}\right)^3}} = \sqrt[3]{26 - 15\sqrt{3}}. \]

  Samostatně zjednodušíme vzniklé odmocniny. Předpokládejme, že

  \[ \small \begin{eqnarray} \sqrt[3]{26 + 15\sqrt{3}} &=& a + b\sqrt{3},\\ \sqrt[3]{26 - 15\sqrt{3}} &=& a - b\sqrt{3}. \end{eqnarray} \]

  Rovnice vynásobíme

  \[ \small \underbrace{\sqrt[3]{26^2 - 15^2 {\cdot} 3}}_{1} = a^2 - 3b^2. \] Zkusíme řešení uhádnout, není náhodou \(a=2\), \(b=1\)? Zkusme dosadit \[ \small \begin{eqnarray} \sqrt[3]{26 + 15\sqrt{3}} &\overset{?}{=}& 2 + \sqrt{3},\\ \sqrt[3]{26 - 15\sqrt{3}} &\overset{?}{=}& 2 - \sqrt{3}. \end{eqnarray} \]

  Umocněním rovnic se snadno přesvědčíme, že jsme se trefili.

  Máme tedy \[ \begin{eqnarray} u &=& 2 + \sqrt{3}, \\ v &=& 2 - \sqrt{3}. \end{eqnarray} \]

  Určíme všechna řešení

  \[ \small \begin{eqnarray} y_1 &=& u + v = 2 + \sqrt{3} + 2 - \sqrt{3} = 4, \\ y_2 &=& \varepsilon u + \varepsilon^2 v = \left(-\frac{1}{2}+\frac{\sqrt{3}}{2} i\right) \left(2 + \sqrt{3}\right) + \left(- \frac{1}{2}-\frac{\sqrt{3}}{2} i\right) \left(2 - \sqrt{3}\right) = \\ &=& -2 + 3i,\\ y_3 &=& \varepsilon^2 u + \varepsilon v = \left(-\frac{1}{2}-\frac{\sqrt{3}}{2} i\right) \left(2 + \sqrt{3}\right) + \left(- \frac{1}{2}+\frac{\sqrt{3}}{2} i\right) \left(2 - \sqrt{3}\right) =\\ &=& -2 - 3i. \end{eqnarray} \]

  Rovnice má reálný kořen \(4\) a komplexní kořeny \(-2 + 3i\) a \(-2 - 3i\).

• Nápověda 3 – návrat k substituci

  V minulé sekci jsme našli kořeny

  \[ y_1 = 4, \qquad y_2 = -2 + 3i, \qquad y_3 = -2 - 3i. \]

  To jsou ale kořeny redukované kubické rovnice. Nalezněte kořeny zadané kubické rovnice. Vraťte se k příslušnému substitučnímu vztahu.

• Řešení nápovědy 3 – návrat k substituci

  Kořeny

  \[ y_1 = 4, \qquad y_2 = -2 + 3i, \qquad y_3 = -2 - 3i. \]

  přepočítáme pomocí substitučního vztahu

  \[ x=y-1 \]

  na

  \[ x_1 = 3, \qquad x_2 = -3 + 3i, \qquad x_3 = -3 - 3i, \]

  což jsou kořeny zadané kubické rovnice

  \[x^3 + 3x^2 - 54 = 0.\]

  Poznámka: vidíme, že dvojice komplexních kořenů je stále vzájemně komplexně sdružená. Musí být, neboť i původní rovnice má reálné koeficienty.

• Odpověď

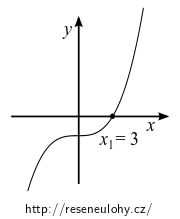
  Kubická rovnice \[x^3 + 3x^2 - 54 = 0\] má jeden kořen reálný a dvojici komplexních kořenů \[ x_1 = 3, \qquad x_2 = -3 + 3i, \qquad x_3 = -3 - 3i. \] Kořeny jsou nulové body kubické funkce tohoto typu