Sbírka řešených úloh

Řetězový zlomek zlatého čísla

Úloha číslo: 1604

• Co je řetězový zlomek?

  Řetězovým zlomkem čísla \(x\) rozumíme výraz typu

  \[ \begin{equation} x= x_0 + \cfrac{1}{x_1 + \cfrac{1}{x_2 + \cfrac{1}{x_3 + \cfrac{1}{\ddots+\frac{1}{x_n} } } } } \end{equation}, \quad\text{kde } \begin{array}{l} x_0\in\mathbb{Z},\\ x_i \in \mathbb{N}, ~ i\in\lbrace 1,\ldots,n \rbrace. \end{array} \]

  Právě byl představen konečný řetězový zlomek. Zkráceně jej zapisujeme

  \[ x = [x_0;x_1,x_2,\ldots,x_n]. \]

  Lze uvažovat (nekonečnou) posloupnost konečných řetězových zlomků – vždy přidáme další člen \(x_n\). Tuto posloupnost nazýváme nekonečným řetězovým zlomkem a zkráceně zapisujeme

  \[ x = [x_0;x_1,x_2,x_3,\ldots]. \]

  Řetězové zlomky reprezentují nějaké číslo \(x\), viz další tvrzení.

  ---

  Pro (ne)periodičnost a (ne)konečnost řetězových zlomků reálných čísel platí:

  \[\small \text{Pro }x\in \left\{ \begin{array}{c} \mathbb{Q} \\ \mathbb{K} \\ \mathbb{R} \setminus \left( \mathbb{K} \cup \mathbb{Q}\right) \end{array} \right\} \text{existuje} \left\{ \begin{array}{l} \text{konečný} \\ \text{nekonečný, periodický} \\ \text{nekonečný, neperiodický} \end{array} \right\} \begin{array}{c} \text{řetězový zlomek.}\\ \end{array} \]

  Množina \(\mathbb{K}\) značí tzv. kvadratické iracionality – čísla tvaru \(\frac{p\pm\sqrt{n}}{q}\), kde \(p,q\in\mathbb{Z}, n\in\mathbb{N}, \sqrt{n} \not\in \mathbb{Q}.\)

• Nápověda 1 – řetězový zlomek

  Rozveďte číslo \(\small\frac{1}{2}(a + \sqrt{a^2 + 4})\) v řetězový zlomek. Jde zjevně o kvadratickou iracionalitu, takže usilujte o nekonečný periodický řetězový zlomek.

• Řešení nápovědy 1 – řetězový zlomek

  Provádějme úpravy, které povedou na tvar řetězového zlomku, podobně jak jsme tomu činili v úlohách zde a zde.

  \[ \frac{1}{2}\left(a+\sqrt{a^2+4}\right) = a + \frac{1}{2}\left(\sqrt{a^2+4} - a\right) = a + \cfrac{1}{\color{maroon}{\frac{2}{\sqrt{a^2+4} - a}}} \overset{\text{ozn.}}{=} a+\frac{1}{\color{maroon}{\gamma}}. \]

  Pokusme se dále přetvořit výraz označený \(\gamma\) do podoby řetězového zlomku a to tak, aby v upraveném výrazu vzniklo opět \(\gamma\), tj.

  \[ \gamma = \frac{2}{\sqrt{a^2+4}-a}\cdot \frac{\sqrt{a^2+4}+a}{\sqrt{a^2+4}+a}= \frac{\sqrt{a^2+4}+\color{blue}{a}}{2}= \] \[ =\frac{\color{blue}{2a}+\sqrt{a^2+4}\color{blue}{-a}}{2}= a+\frac{\sqrt{a^2+4}-a}{2}= a+\frac{1}{\gamma}. \]

  Máme tedy vztah

  \[ \gamma = a + \frac{1}{\gamma}, \]

  jehož opakovanou aplikací „nagenerujeme“ celý řetězový zlomek

  \[ \frac{1}{2}\left(a+\sqrt{a^2+4}\right)= a+\frac{1}{\gamma}= a+\cfrac{1}{a+\cfrac{1}{\gamma}}= a+\cfrac{1}{a+\cfrac{1}{a+\cfrac{1}{\gamma}}}= \] \[ =a+\cfrac{1}{a+\cfrac{1}{a+\cfrac{1}{\ddots}}} = \left[a;a,a,\ldots \right] = \left[a;\overline{a}\right]. \]

  Tj. \(\left[a;\overline{a}\right]\) je nekonečný periodický řetězový zlomek čísla \(\small\frac{1}{2}\left(a+\sqrt{a^2+4}\right)\).

• Nápověda 2 – aproximace zlatého čísla

  Na základě nalezeného obecného řetězového zlomku určete řetězový zlomek zlatého čísla \(\frac{1+\sqrt{5}}{2}\). Následně hledejte konečné řetězové zlomky s minimálním počtem členů, potřebné k aproximaci s přesností na čtyři desetinná místa. Hodnoty řetězových zlomků porovnávejte s kalkulačkou.

• Řešení nápovědy 2 – aproximace zlatého čísla

  Řetězový zlomek čísla \(\frac{1+\sqrt{5}}{2}\) dostaneme dosazením \(a=1\).

  \[ \frac{1}{2}\left(1+\sqrt{1^2+4}\right)= \frac{1+\sqrt{5}}{2}= 1+ \cfrac{1}{1 + \cfrac{1}{1 + \cfrac{1} \ddots } } = \left[1;1,{}1,\ldots \right] = \left[1;\overline{1}\right] \]

  Berme postupně konečné řetězové zlomky s jedním, dvěma, třemi atd. členy a jejich hodnoty porovnávejme s „kalkulačkovou“ hodnotou. Pro výpočet jednotlivých sblížených zlomků užijeme metodu popsanou zde.

  \[ \begin{array}{r|r|r|r|l|l} \small{\text{index}} & x_i & a_i & b_i & \text{hodnota} & \text{kalkulačka} \\ \small{0} & 1 & 1 & 1 & \small{\frac{1}{1}} = 1 & 1{,}61803\\ \small{1} & 1 & 2 & 1 & \small{\frac{2}{1}} = 2 & 1{,}61803\\ \small{2} & 1 & 3 & 2 & \small{\frac{3}{2}} = 1{,}50000 & 1{,}61803\\ \small{3} & 1 & 5 & 3 & \small{\frac{5}{3}} \doteq 1{,}66667 & 1{,}61803\\ \small{4} & 1 & 8 & 5 & \small{\frac{8}{5}} = 1{,}60000 & 1{,}61803\\ \small{5} & 1 & 13 & 8& \small{\frac{13}{8}} = 1{,}62500 & 1{,}61803\\ \small{6} & 1 & 21 &13& \small{\frac{21}{13}} \doteq 1{,}61538 & 1{,}61803\\ \small{7} & 1 & 34 &21& \small{\frac{34}{21}} \doteq 1{,}61905 & 1{,}61803\\ \small{8} & 1 & 55 &34& \small{\frac{55}{34}} \doteq 1{,}61905 & 1{,}61803\\ \small{9} & 1 & 89 &55& \small{\frac{89}{55}} \doteq 1{,}61905 & 1{,}61803\\ \small{10}& 1 & 144 & 89 & \small{\frac{144}{89}} \doteq 1{,}61905 & 1{,}61803 \\ \small{11}& 1 & 233 & 144 & \small{\frac{233}{144}} \doteq 1{,}61806 & 1{,}61803 \\ \small{12}& 1 & 377 & 233 & \small{\frac{377}{233}} \doteq \color{maroon}{1{,}6180}3 & \color{maroon}{1{,}6180}3 \end{array} \]

  Reálné číslo \(\frac{1+\sqrt{5}}{2}\) lze aproximovat zlomkem \(\frac{377}{233}\). Hodnotu odmocniny dostaneme s přesností na čtyři desetinná místa.

• Odpověď

  Řetězový zlomek čísla \(\small\frac{1}{2}(a + \sqrt{a^2 + 4})\) je

  \[a+\cfrac{1}{a+\cfrac{1}{a+\cfrac{1}{\ddots}}} = \left[a;a,a,\ldots \right] = \left[a;\overline{a}\right].\]

  Racionální aproximace zlatého čísla \(\small\frac{1+\sqrt{5}}{2}\) s přesností na čtyři desetinná místa

  \[ \frac{1+\sqrt{5}}{2} ~\approx~ \left[ 1;1{},1{},1{},1{},1{},1{},1{},1{},1{},1{},1{},1 \right] = \frac{377}{233}. \]

• Komentář: Co je zlaté číslo?

  Říkáme, že úsečka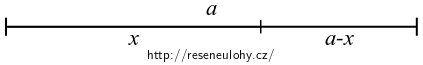

  

  je rozdělena v poměru zlatého řezu, jestliže platí

  \[ a:x = x:(a-x), \tag{1}\]

  tedy jestliže „celá k delší se má jako delší ke kratší“.

  Poměr \(a:x\) pak nazveme zlatým číslem.

  Označíme-li \(\varphi=\frac{a}{x}\), pak z podmínky (1) máme \[ \varphi = \frac{x}{\varphi x - x} \quad \Rightarrow \quad \varphi = \frac{1}{\varphi - 1}, \] což je kvadratická rovnice \[ \varphi^2 - \varphi - 1 = 0, \] přičemž pouze její kladný kořen \[ \varphi = \frac{1+\sqrt{5}}{2} \] má geometrický význam a představuje hledané zlaté číslo.

  ---

  Se zlatým řezem se pojí některé zajímavostí. Pro ilustraci uveďme následující: máme-li výkres se stranami \(a,x\) v poměru zlatého řezu a odřízneme-li z něj čtverec o straně \(x\), zůstane opět výkres se stranami v poměru zlatého řezu. Takto lze samozřejmě odřezávat i dále.