Sbírka řešených úloh

Počty reálných kořenů kubické rovnice

Úloha číslo: 1608

• Teorie

  Kořenům kubické rovnice se věnuje úloha Cardanovy vzorce.

• Nápověda

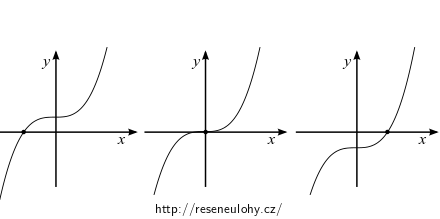
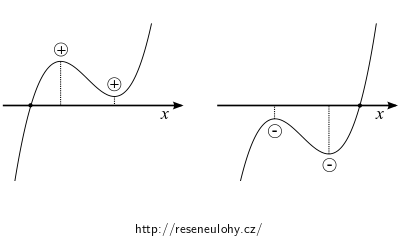
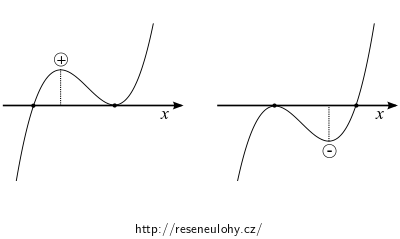
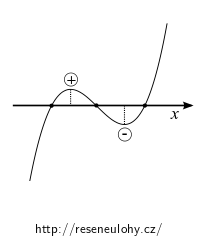
  Uvažujte kubickou funkci \(f(x) = x^2 + px + q\) a nalezněte její maxima. Určete funkční hodnoty v těchto maximech a vypočtěte jejich součin. Proveďte diskuzi o počtu reálných kořenů, načrtněte ilustrační obrázky.

• Řešení nápovědy

  Proveďme rozbor kubické funkce \(f(x) = x^3 + px + q\).

  Hledejme extrémy \[ f^\prime(x) = 3x^2 + p = 0 \quad \Rightarrow \quad x_{1{,}2}=\pm\sqrt{-\frac{p}{3}}, \] \[ f^{\prime\prime}(x) = 6x = 0, \] \[ f^{\prime\prime\prime}(x) = 6 \neq 0. \]

  Rozlišíme dva případy

  \[ \begin{array}{lll} \text{a) pro} & p \gt 0 & \text{není extrém;}~ f^\prime(x)\gt 0,\mathrm{tj.}~f \text{ je rostoucí} ,\\ \text{b) pro} & p \lt 0 & \text{dva extrémy};~\text{v }x_1\text{ minimum},\text{ v }x_2\text{ maximum}. \end{array} \]

  a) Případ \(p\gt 0\): rostoucí na celém \(\mathbb{R}\)

  Funkce je rostoucí na celém \(\mathbb{R}\) a je spojitá. Má tedy jeden reálný kořen. Ten je záporný pro \(q\gt 0\), nulový pro \(q= 0\) a kladný pro \(q \lt 0\).

  

  b) Případ \(p\lt 0\): dva extrémy

  Nejprve vypočítáme funkční hodnoty v extrémních bodech

  \[ \begin{eqnarray} f(x_1) &=& \sqrt{\left(-\frac{p}{3}\right)^3} + p\sqrt{-\frac{p}{3}} + q = \sqrt{-\frac{p}{3}}\left(-\frac{p}{3} + p\right) + q,\\ f(x_2) &=& -\sqrt{\left(-\frac{p}{3}\right)^3} - p\sqrt{-\frac{p}{3}} + q = -\sqrt{-\frac{p}{3}}\left(-\frac{p}{3} + p\right) + q. \end{eqnarray} \]

  Určíme součin těchto funkčních hodnot

  \[ f(x_1) f(x_2) = \left[ \sqrt{-\frac{p}{3}}\left(-\frac{p}{3} + p\right) + q\right] \left[ -\sqrt{-\frac{p}{3}}\left(-\frac{p}{3} + p\right) + q \right]= \] \[ = -\sqrt{-\frac{p}{3}} \sqrt{-\frac{p}{3}} p p \left(1 - \frac{1}{3}\right)^2 + 0 + 0 + q^2 = \] \[ =4\left(\frac{q}{2}\right)^2 + 4\left(\frac{p}{3}\right)^3 = 4D. \]

  Co nám říká odvozený vztah \(f(x_1)f(x_2) = 4D\) pro polohy extrémů a následně pro počty kořenů?

  • Bude-li \(D\gt 0\), pak jsou funkční hodnoty obou extrémů buďto kladné nebo záporné. Kubická rovnice má jeden reálný kořen.

  

  • Bude-li \(D = 0\), pak je funkční hodnota jednoho extrému nulová a druhého záporná nebo kladná. Kubická rovnice má jeden reálný jednoduchý a jeden reálný dvojnásobný kořen.

  

  • Bude-li \(D \lt 0\), pak je funkční hodnota jednoho extrému kladná a druhého záporná. Kubická rovnice má tři různé reálné kořeny.

  

  Poslednímu případu, kdy \(D\lt 0\), se říká casus irreducibilis, v překladu „nezjednodušitelný případ“. Při hledání kořenů se v Cardanových vzorcích objevují komplexní „nepřístojnosti“, ač je situace funkce v grafu velmi příznivá, vždyť má rovnice tři různé reálné kořeny.

• Odpověď

  Pro kubickou rovnici v redukovaném tvaru

  \[ x^3 + px + q = 0 \]

  jejímž diskriminantem rozumíme

  \[D = \left(\frac{q}{2}\right)^2 + \left(\frac{p}{3}\right)^3,\]

  můžou nastat následující možnosti:

  \[ \begin{array}{lll} p\gt 0 & q = 0 & \text{1 nulový reálný kořen,} \\ & q \gt 0 & \text{1 záporný reálný kořen,} \\ & q \lt 0 & \text{1 kladný reálný kořen,} \\ p\lt 0 & D \gt 0 & \text{1 reálný kořen,} \\ & D = 0 & \text{1 reálný jednoduchý, 1 reálný dvojnásobný kořen,} \\ & D \lt 0 & \text{3 různé reálné kořeny.} \end{array} \]