Sbírka řešených úloh

Nerovnost mezi průměry

Úloha číslo: 1601

• Teorie: jak se počítají průměry

  Aritmetický průměr dvou čísel získáme tak, že jejich součet vydělíme dvěma:

  \[ AP(a,b) = \frac{a+b}{2}. \]

  Geometrický průměr dvou čísel získáme tak, že jejich součin odmocníme:

  \[ GP(a,b) = \sqrt{ab}. \]

  Harmonický průměr získáme jako převrácenou hodnotu aritmetického průměru jejich převrácených hodnot:

  \[ HP(a,b) = \frac{1}{\frac{\frac{1}{a}+\frac{1}{b}}{2}} = \frac{2ab}{a+b}. \]

• a) Nápověda – algebraický důkaz

  Při dokazování nerovností je třeba vyjít z nějakého šikovného pravdivého tvrzení. Prozraďme, že k cíli snadno vedoucí bude nerovnost \[ (\sqrt{a} - \sqrt{b})^2 \ge 0, \] která je jistě splněna pro všechna námi uvažovaná \(a,b\).

• a) Řešení nápovědy – algebraický důkaz

  Vyjdeme z nerovnosti, která platí pro všechna námi uvažovaná \(a,b\). \[ \begin{eqnarray} \left(\sqrt{a} - \sqrt{b}\right)^2 &\ge& 0 \\ a - 2 \sqrt{ab} + b &\ge& 0 \\ a + b &\ge& 2 \sqrt{ab} \\ \frac{a + b}{2} &\ge& \sqrt{ab} \tag{1} \end{eqnarray} \] Úpravami jsme tak dostali nerovnost aritmetického a geometrického průměru \[ AP(a,b) \ge GP(a,b). \tag{2}\] Nerovnost (1) můžeme dále upravit tak, abychom na pravé straně získali vyjádření harmonického průměru. \[ \begin{eqnarray} \frac{a + b}{2} &\ge& \sqrt{ab} \qquad | \cdot \sqrt{ab} \\ \frac{a + b}{2}\sqrt{ab} &\ge& ab \quad\qquad | \cdot \frac{2}{a+b}\\ \sqrt{ab} &\ge& \frac{2ab}{a+b} \end{eqnarray} \] Dostali jsme další nerovnost, nyní geometrického a harmonického průměru \[ GP(a,b) \ge HP(a,b). \tag{3}\] Odvozené nerovnosti (2),(3) dohromady představují dokazované tvrzení. \[ AP(a,b) \ge GP(a,b) \ge HP(a,b)\qquad\square \]

• b) Nápověda – grafický důkaz

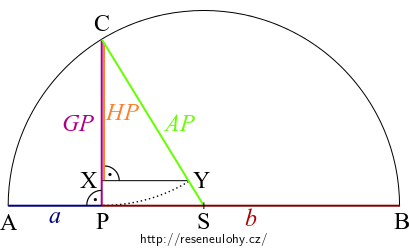
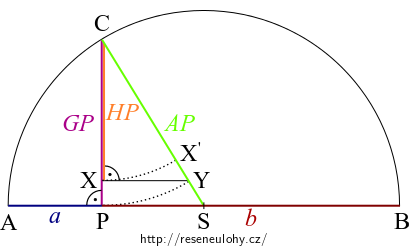
  Nalezněte jednotlivé průměry v půkružnici sestrojené nad úsečkou délky \(a+b\). Užijte Eukleidovu větu o výšce a podobnost trojúhelníků.

• b) Řešení nápovědy – grafický důkaz

  Sestrojíme půlkružnici nad průměrem délky \(a+b\). Libovolný poloměr této půlkružnice je aritmetickým průměrem, neboť \(r=d/2 = (a+b)/2\).

  

  Sestrojíme-li kolmici v bodě \(\mathrm{P}\) na \(\mathrm{AB}\), má vzniklá úsečka \(\mathrm{PC}\) délku geometrického průměru, neboť z Eukleidovy věty o výšce je \(|\mathrm{PC}|=\sqrt{ab}\).

  Zbývá nalézt průměr harmonický. Všiměme si podobnosti

  \[ \triangle \mathrm{PSC} \sim \triangle \mathrm{XYC}, \]

  odkud pro poměr stran

  \[ \frac{|\mathrm{PC}|}{|\mathrm{SC}|} = \frac{|\mathrm{XC}|}{|\mathrm{YC}|} \]

  a vyjádřením a dosazením příslušných průměrů

  \[ |\mathrm{XC}| = \frac{|\mathrm{PC}|}{|\mathrm{SC}|} |\mathrm{YC}| = \frac{GP}{AP}GP = \frac{GP^2}{AP} = \frac{ab}{\frac{a+b}{2}} = \frac{2ab}{a+b} = HP. \]

  Úsečka \(\mathrm{XC}\) má tedy význam harmonického průměru.

  Pro porovnání jednotlivých průměrů můžeme ještě přenést harmonický průměr na polopřímku \(\mathrm{CS}\), na které pak budeme mít všechny tři průměry.

  

  Zjevně

  \[|\mathrm{CS}|\ge|\mathrm{CY}|\ge|\mathrm{CX^\prime}|,\]

  tedy

  \[AP(a,b) \ge GP(a,b) \ge HP(a,b)\qquad\square\]

• Odpověď

  Nerovnosti mezi aritmetickým, geometrickým a harmonickým průměrem jsme ukázali algebraicky a dále jsme příslušné průměry interpretovali v půlkružnici nad průměrem délky \(a+b\).