Sbírka řešených úloh

Kubická rovnice I.

Úloha číslo: 1609

• Nápověda 1 – počet a typ kořenů

  Jaká je hodnota \(p,q\) a \(D\)? Co to znamená pro počty a typy kořenů? Viz úloha Počty reálných kořenů kubické rovnice.

• Řešení nápovědy 1 – počet a typ kořenů

  Zadaná kubická rovnice je přímo v redukovaném tvaru, tedy jednoduše

  \[ p = -3,\qquad q = -2. \] Diskriminant této kubické rovnice je \[ D = \left(\frac{q}{2}\right)^2 + \left(\frac{p}{3}\right)^3 = \left(\frac{-2}{2}\right)^2 + \left(\frac{-3}{3}\right)^3 = 1-1 = 0. \]

  Užijeme závěrů z úlohy Počty reálných kořenů kubické rovnice. Neboť je koeficient \(p\) záporný, nabývá kubická funkce dvou extrémů. Diskriminant je nulový – máme jeden reálný jednoduchý a jeden reálný dvojnásobný kořen.

• Nápověda 2 – hledání kořenů

  Pomocí Cardanových vzorců nalezněte řešení kubické rovnice.

  Cardanovy vzorce:

  \[ \begin{eqnarray} x_1 &=& u + v, \\ x_2 &=& \varepsilon u + \varepsilon^2 v, \\ x_3 &=& \varepsilon^2 u + \varepsilon v, \end{eqnarray} \] \[\small\text{kde }\quad u = \sqrt[3]{-\frac{q}{2} + \sqrt{\left(\frac{q}{2}\right)^2 + \left(\frac{p}{3}\right)^3}}, \qquad v = \sqrt[3]{-\frac{q}{2} - \sqrt{\left(\frac{q}{2}\right)^2 + \left(\frac{p}{3}\right)^3}},\] \[ \text{a }\quad\small\varepsilon = -\frac{1}{2}+\frac{\sqrt{3}}{2} i. \]

• Řešení nápovědy 2 – hledání kořenů

  Pomocí Cardanových vzorců nalezneme kořeny kubické rovnice. Nejprve určíme \(u,v\).

  Již víme, že \(p=-3\), \(q=-2\) a také jsme vypočítali \(D=0\). Proto

  \[u = \sqrt[3]{-\frac{q}{2} + \sqrt{\underbrace{\left(\frac{q}{2}\right)^2 + \left(\frac{p}{3}\right)^3}_{0}}} = \sqrt[3]{-\frac{-2}{2}} = 1, \] \[v = \sqrt[3]{-\frac{q}{2} - \sqrt{\underbrace{\left(\frac{q}{2}\right)^2 + \left(\frac{p}{3}\right)^3}_{0}}} = \sqrt[3]{-\frac{-2}{2}} = 1. \]

  K sestavení všech řešení budeme potřebovat druhou mocninu \(\varepsilon\). Pro jednou ji vypočítáme

  \[ \small \varepsilon^2 = \left(-\frac{1}{2}+\frac{\sqrt{3}}{2} i\right)^2 = \frac{1}{4} -\frac{\sqrt{3}}{2}i - \frac{3}{4} = -\frac{1}{2}-\frac{\sqrt{3}}{2} i. \]

  Dále si ji budeme určitě pamatovat, neboť jak vyplývá z geometrické interpretace násobení komplexních čísel, je třeba se v Gaussově rovině pootočit o \(\frac{2\pi}{3}\), čemuž odpovídá pouze změna znaménka u imaginární části.

  Určíme všechna řešení

  \[ \begin{eqnarray} x_1 &=& u + v = 1 + 1 = 2, \\ x_2 &=& \varepsilon u + \varepsilon^2 v = -\frac{1}{2}+\frac{\sqrt{3}}{2} i - \frac{1}{2}-\frac{\sqrt{3}}{2} i = -1, \\ x_3 &=& \varepsilon^2 u + \varepsilon v= -\frac{1}{2}-\frac{\sqrt{3}}{2} i - \frac{1}{2}+\frac{\sqrt{3}}{2} i = -1. \end{eqnarray} \]

  Rovnice má jeden jednoduchý kořen \(x_1 = 2\) a jeden dvojnásobný kořen \(x_{2{,}3}=-1\).

• Odpověď

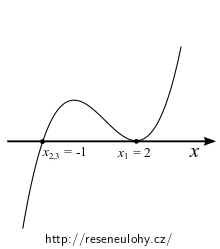
  Kubická rovnice

  \[ x^3 - 3x - 2 = 0 \]

  má jeden jednoduchý kořen \(x_1 = 2\) a jeden dvojnásobný kořen \(x_{2{,}3}=-1\).