Sbírka řešených úloh

Součet n členů aritmetické posloupnosti

Úloha číslo: 1597

• a) Nápověda – rekurentní vztah

  Napište vzorec pro $n+1$ člen a „identifikujte“ v něm člen $n$-tý.

• a) Řešení nápovědy – rekurentní vztah

  Ve výrazu pro $n+1.$ člen nalezneme vyjádření členu $n$-tého $$a_{\color{maroon}{n+1}} = a_1 + \big((\color{maroon}{n+1})-1\big)d = \underbrace{a_1 + (n-1)d}_{a_n} + d = a_n+d.$$ Hledaný rekurentní vztah je tedy $$a_{n+1} = a_n + d, \qquad \forall n \ge 1,$$

  přitom je udán první člen $a_1$.

  Z rekurentního vztahu plyne, že se jedná o aritmetickou posloupnost s konstantní diferencí $d$ a prvním členem $a_1$.

• b) Nápověda – vyjádření součtu

  Zapište součet prvních $n$ členů aritmetické posloupnosti. K tomuto součtu pak přičtěte tentýž součet, ale v obráceném pořadí celé sečtěte. Získáte tak $2s_n$.

• b) Řešení nápovědy – vyjádření součtu

  Pomocí zadání aritmetické posloupnosti můžeme hledaný součet

  $$s_n = \sum_{i=1}^n a_i = a_1 + a_2 + a_3 + ~\ldots~ + a_n$$

  přepsat pomocí prvního členu a diference

  $$s_n = a_1 + (a_1 + d) + (a_1 + 2d) + \ldots + \big(a_1 + (n-1)d\big).$$

  Zapišme tento součet dvakrát pod sebe, v druhém řádku v obráceném pořadí

  $$\small{ \begin{array}{r} 2s_n = \\ + \end{array} \begin{array}{c} a_1 \\ a_1 + (n-1)d \end{array} \begin{array}{c} +\\ +\\ \end{array} \begin{array}{c} a_1 + d \\ a_1 + (n-2)d \end{array} \begin{array}{c} +\\ +\\ \end{array} \begin{array}{c} a_1 + 2d \\ a_1 + (n-3)d \end{array} \begin{array}{c} +\,\ldots\,+\\ +\,\ldots\,+\\ \end{array} \begin{array}{c} a_1 + (n-1)d +\\ a_1 \end{array}}.$$

  Vidíme, že součet čísel v každém sloupci je stejný a to $2a_1 + (n-1)d$. Těchto sloupců je zde zřejmě $n$, proto

  $$2s_n = n \big[2a_1 + (n-1)d\big]$$

  a tedy

  $$s_n = \frac{1}{2} n \big[2a_1 + (n-1)d\big].$$

  Můžeme také nalézt vyjádření pomocí prvního a $n$-tého členu

  $$s_n = \frac{1}{2} n \big[a_1 + \underbrace{a_1 + (n-1)d}_{a_n}\big]= \frac{1}{2} n (a_1 + a_n).$$

• c) Nápověda – konvergence řady

  Rozvažte konvergenci aritmetické řady, tj. řady $$\sum_n^\infty \big[a_1 + (n-1)d\big].$$

• c) Řešení nápovědy – konvergence řady

  Pro aritmetickou řadu

  $$\sum_n^\infty \big[a_1 + (n-1)d\big]$$

  již známe součet $n$ členů, tj. posloupnost částečných součtů. Podíváme se na její limitu

  $$\lim_{n\to \infty} s_n = \lim_{n\to \infty} \frac{1}{2} n \big[2a_1 + (n-1)d\big] = \left\{ \begin{array}{l l} 0 & \quad \text{pro }q=a_1=0,\\ \pm\infty & \quad \text{pro } q\neq0 \vee a_1\neq0. \end{array} \right.$$

  Aritmetická řada tedy diverguje k $+\infty$ nebo $-\infty$ až na speciální případ nulové řady, kdy je součet $0$.

• Komentář – součet pomocí „kamínků“

  Součet prvních $n$ členů aritmetické posloupnosti s $a_1 = 1$ a $d=1$ můžeme nalézt geometrickým znázorněním pomocí tzv. trojúhelníkových čísel.

  

  Trojúhelník „kamínků“ představuje hledaný součet $$s_n = 1 + 2 + \ldots + n.$$ Sečteme-li tyto dva trojúhelníky, dostáváme obdelníkové číslo $n\times (n+1)$, tedy $$2s_n = n(n+1).$$ Odtud snadno pro hledaný součet $$s_n = \frac{1}{2}n (1+n).$$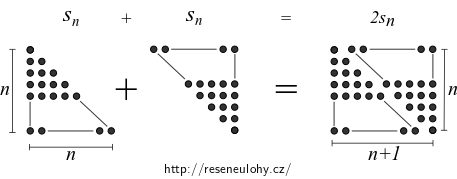

  Námět čerpán z publikace „Hrdinský věk řecké matematiky“ J. Bečváře (dostupné online zde). V této knize naleznete mimo jiné odvození mnoha dalších identit pomocí figurálních čísel.

• Odpověď

  a) Rekurentní vyjádření zadané posloupnosti je

  $$a_{n+1} = a_n + d, \quad \forall n \ge 1,$$

  přičemž $a_1,d$ jsou pevně volená.

  Jedná se tedy o aritmetickou posloupnost s konstantní diferencí (1. řádu).

  b) Součet prvních $n$ členů lze vyjádřit pomocí $a_1$ a $d$

  $$s_n = \frac{1}{2} n \big[2a_1 + (n-1)d\big],$$

  případně pomocí $a_1$ a $a_n$

  $$s_n = \frac{1}{2} n (a_1 + a_n).$$

  c) Aritmetická řada diverguje k $\pm \infty$ kromě nulové řady. Ta konverguje k $0$.