Kondenzátor s deskou na pružině
Úloha číslo: 81
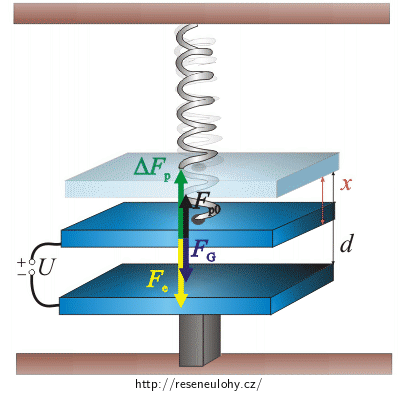
Vzduchový kondenzátor je tvořen dvěma rovnoběžnými vodorovnými deskami o plošném obsahu S = 100 cm2. Dolní deska je upevněna v držáku, horní je zavěšena na pružině s tuhostí k = 1 N m−1, která umožňuje pohyb desky nahoru a dolů (desky zůstávají rovnoběžné). K deskám připojíme zdroj, jehož napětí budeme velmi pomalu zvětšovat. Při nulovém napětí je vzdálenost desek d = 2 mm, při zvětšování napětí se budou desky přibližovat.
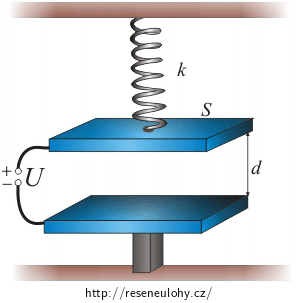
a) Odvoďte vztah mezi napětím U a posunutím x horní desky z počáteční polohy, při kterém bude v rovnováze přitažlivá síla desek a síla pružiny.
b) Nakreslete graf závislosti posunutí desky x na napětí U.
c) Diskutujte, ve kterých případech je rovnovážná poloha desek stabilní a ve kterých labilní.
d) Jaké je maximální napětí, pro které jsou desky ve stabilní rovnováze? V jaké vzdálenosti jsou desky při tomto napětí?
a) Nápověda
Je-li deska v klidu, musí být výslednice sil působících na desku nulová. Uvědomte si, jaké všechny síly na desku působí?a) Nápověda
Jak se mění jednotlivé síly působící na horní desku, jestliže připojíme desky kondenzátoru ke zdroji napětí, které můžeme měnit?
Obrázek působících sil
a) Rozbor
Pokud není kondenzátor připojený ke zdroji napětí, působí na horní desku tíhová síla a síla pružnosti, která se snaží vrátit pružinu do nenataženého stavu. Protože je deska v klidu, je výslednice těchto dvou sil rovna nule.
Připojíme-li desky kondenzátoru ke zdroji napětí, začne na horní desku působit přitažlivá elektrická síla dolní desky. Deska se začne posouvat směrem dolů a tím bude natahovat pružinu. Čím větší bude prodloužení pružiny, tím větší bude změna síly pružnosti. Jsou-li desky v rovnovážné poloze, je elektrická síla stejně velká jako změna síly pružnosti (výslednice těchto sil je opět nulová).
Z rovnosti elektrické síly a změny síly pružnosti vyjádříme hledané napětí.
a) Řešení: Odvození vztahu mezi napětím a posunutím desky
Je-li napětí na deskách nulové, působí na horní desku tíhová síla a síla pružnosti. Deska je v klidu, proto je výslednice těchto dvou sil nulová.
Připojíme-li desky ke zdroji napětí, začnou se desky přitahovat elektrickou silou \(\vec{F}_\mathrm{e}\) a horní deska se začne posouvat směrem dolů. Pružina se bude natahovat a síla, kterou působí na desku, se bude zvětšovat. Čím více pružinu natáhneme (čím větší bude posunutí), tím vetší bude síla pružnosti.
Síla pružnosti se zvětší o
\[\mathrm{\Delta} F_\mathrm{p}\,=\,kx\,,\tag{1}\]kde k je tuhost pružiny a x je posunutí horní desky.
Nyní si vyjádříme velikost elektrické síly Fe, kterou na horní desku působí dolní deska kondenzátoru. Pro tuto sílu platí vztah:
\[F_\mathrm{e}\,=\,Q \frac{E}{2}\,,\tag{*}\]kde E je celková intenzita pole mezi deskami kondenzátoru a \(\frac{E}{2}\) je velikost intenzity elektrického pole, které vytváří jen spodní deska. Podrobněji je vztah celkové intenzity a intenzity pole od jedné desky vysvětlen v úloze Síla působící na desky kondenzátoru.
Intenzita elektrického pole E mezi deskami kondenzátoru závisí na napětí U a vzdálenosti desek l:
\[E\,=\,\frac{U}{l}\,.\]Při nulovém napětí jsou desky ve vzdálenosti d. Připojíme-li desky ke zdroji napětí, bude se horní deska posouvat. Vzdálenost desek d se zmenší o posunutí x horní desky a pro vzdálenost desek bude platit l = d − x.
Intenzita pole mezi deskami je tedy:
\[E\,=\,\frac{U}{d-x}\,.\]Tento vztah dosadíme do vzorce pro elektrickou sílu (*):
\[F_\mathrm{e} \,=\, Q\frac{E}{2}\,=\,Q\frac{U}{2\left(d-x\right)}\,.\]Náboj na desce kondenzátoru je přímo úměrný napětí a kapacitě kondenzátoru \(Q=CU\):
\[ F_\mathrm{e}\,=\,\frac{CU^2}{2\left(d-x\right)}\,.\tag{**}\]Nyní si ještě vyjádříme kapacitu deskového kondenzátoru, která závisí na ploše desek S, permitivitě vakua ε0 a vzdálenosti desek d − x podle vzorce:
\[C\,=\,\frac{\varepsilon_0 S}{l}\,=\,\frac{\varepsilon_0 S}{d-x}.\]Kapacitu dosadíme do vztahu pro elektrickou sílu (**):
\[F_\mathrm{e}\,=\,\frac{\varepsilon_0 S U^2}{2\left(d-x\right)^2}\,.\tag{2}\]Získali jsme vztah pro elektrickou sílu, která působí na horní desku.
Zajímá nás stav, kdy je přitažlivá elektrická síla působící na horní desku a zvětšení síly pružnosti v rovnováze:
\[F_\mathrm{e}\,=\,\mathrm{\Delta}F_\mathrm{p}\,.\]Dosadíme vztah pro elektrickou sílu (2) a přírůstek síly pružnosti (1):
\[\frac{\varepsilon_0 S U^2}{2\left(d-x\right)^2}\,=\,kx.\]Chceme vyjádřit vztah mezi napětím U a posunutím x. Budeme tedy rovnost upravovat tak, aby na levé straně zůstalo pouze napětí U.
Rovnici vynásobíme výrazem \(\frac{2\left(d-x\right)^2}{\varepsilon_0 S }\):
\[U^2\,=\,\frac{2kx\left(d-x\right)^2}{\varepsilon_0 S }\]a odmocníme:
\[U\,=\,\sqrt{\frac{2kx\left(d-x\right)^2}{\varepsilon_0 S }}\,.\tag{***}\]Získali jsme závislost napětí U na posunutí horní desky x.
b) Nápověda: graf závislosti posunutí na napětí
V části a) jsme si vyjádřili závislost napětí U na posunutí x:
\(U\,=\,\sqrt{\frac{2kx\left(d-x\right)^2}{\varepsilon_0 S }}.\)Do grafu máme ale zakreslit závislost opačnou. Posunutí x však nelze ze vztahu jednoduše vyjádřit.
Zkuste využít souvislosti mezi grafem funkce a grafem funkce k ní inverzní.
b) Řešení: Graf závislosti posunutí na napětí
Napětí závisí na posunutí podle vzorce (***), který jsme si vyjádřili v předchozí části:
\[U\,=\,\sqrt{\frac{2kx\left(d-x\right)^2}{\varepsilon_0 S }}.\]Naším úkolem je však nakreslit graf závislosti posunutí na napětí. Vyjádření posunutí x je velmi složité (člen x je v rovnici ve třetí, druhé i první mocnině). Nicméně pro nakreslení grafu toto vyjádření nepotřebujeme, stačí si uvědomit, že se jedná o navzájem inverzní funkce.
Nakreslíme tedy nejprve závislost napětí na posunutí, kterou máme již vyjádřenou. Poté graf překlopíme podle osy prvního kvadrantu. (Jednodušeji řečeno hodnoty x naneseme na svislou osu a hodnoty U na osu vodorovnou.)
Abychom nakreslili graf závislosti napětí na posunutí, dosadíme do vzorce (***) zadané číselné hodnoty:
\[S\,=\,100\,\mathrm{cm^2}\,=\,0{,}01\,\mathrm{m^2},\] \[k\,=\,1\,\mathrm{Nm^{-1}},\] \[d\,=\,2\,\mathrm{mm}\,=\,2{\cdot}10^{-3}\,\mathrm{m},\] \[\varepsilon_0\,=\,8{,}85{\cdot} 10^{-12}\,\mathrm{ C^2\,N^{-1}\,m^{-2}}.\]Dostáváme závislost:
\[U\,=\,\sqrt{\frac{2 \cdot x \cdot \left(2{\cdot}10^{-3}-x\right)^2}{8{,}85{\cdot} 10^{-12}\cdot 0{,}01 }}.\]Graf zpracujeme na počítači pomocí vhodného tabulkového editoru (např. MS Excel) pro hodnoty posunutí x od 0 mm (desky jsou ve vzdálenosti d) do 2 mm (vzdálenost mezi deskami je nulová).
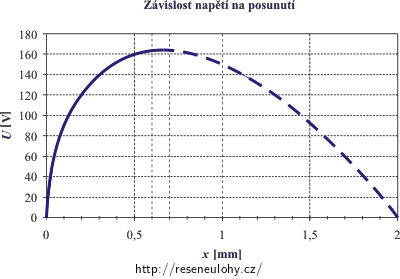
Nyní už můžeme nakreslit hledaný graf závislosti posunutí na napětí. Pozor na čárkovanou část funkce. Protože funkce závislosti napětí na posunutí není prostá, neexistuje tedy inverzní funkce na celém intervalu \( \langle 0\,;2 \rangle \). Do grafu tedy zakreslíme pouze rostoucí část funkce od 0 do maxima.
Zde si můžete stáhnout soubor ve formátu MS Excel, ve kterém naleznete zpracované grafy.
c) Nápověda
Rozmyslete si, jak se mění velikost elektrické síly a síly pružnosti při určité hodnotě napětí v závislosti na posunutí desky.
Nakreslete si graf závislosti velikosti obou sil na posunutí a pomocí něj zkuste vysvětlit stabilitu či labilitu jednotlivých rovnovážných poloh.
c) Rozbor a řešení
Abychom zjistili, proč nemohou desky zůstávat v libovolné stabilní rovnovážné poloze, podívejme se podrobněji na graf závislosti napětí na rovnovážné poloze horní desky (viz graf v oddíle řešení b). Nejdříve se jedná o rostoucí graf, tj. pokud chci dosáhnout většího posunutí, musím na desky přiložit větší napětí. Pro určitou hodnotu posunutí dosáhne napětí svého maxima a poté s rostoucím posunutím klesá. Pro jednu hodnotu napětí máme tedy dvě rovnovážné polohy desky. Jedině v případě maximálního napětí existuje pouze jedna rovnovážná poloha.
Zkusíme zjistit, zda jsou tyto rovnovážné polohy stabilní, nebo labilní. Nakreslíme si vždy pro dané napětí graf závislosti velikosti elektrické síly a síly pružnosti na poloze horní desky.
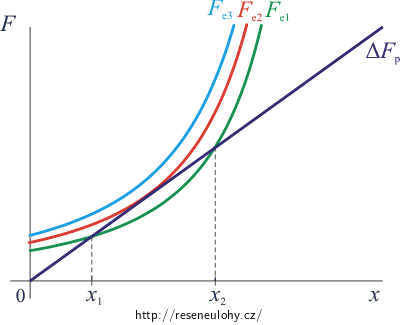
Grafem závislosti velikosti přírůstku síly pružnosti ΔFp na posunutí x
\[\mathrm{\Delta}F_\mathrm{p}\,=\,kx\]je přímka procházející počátkem (v grafu zakreslena fialovou barvou). Protože velikost síly nezávisí na napětí, je tato přímka pro všechna napětí stejná.
Grafem závislosti velikosti elektrické síly Fe na posunutí x
\[F_\mathrm{e}\,=\,\frac{\varepsilon_0 S U^2}{2 \left(d-x\right)^2}\]je křivka, která vypadá podobně jako jedna větev hyperboly. Tvar a poloha této křivky závisí na hodnotě napětí.
Pro maximální napětí má křivka s přímkou jeden společný bod. V grafu je zakreslena červeně. Pro napětí, která jsou menší, mají křivka a přímka dva společné body. Jeden takový případ je zakreslen zeleně. Pro napětí vyšší, než je maximální napětí, křivka nemá s přímkou žádný společný bod (zakresleno modře).
Nyní už můžeme diskutovat, která rovnováha je stabilní a která labilní.
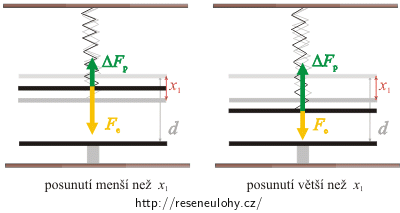
Nejdříve se podíváme na zelenou křivku a její první průsečík s přímkou. V tomto případě se deska ustálí v rovnovážné vzdálenosti x1. Jestliže toto posunutí zmenšíme (část grafu nalevo od průsečíku), bude elektrická síla větší než síla pružnosti. Deska se tedy vrátí zpátky do rovnovážné polohy. Pokud naopak posunutí zvětšíme (část grafu napravo od průsečíku), bude elektrická síla menší než síla pružnosti. Pružina tedy vrátí desku opět do rovnovážné polohy. Obě situace jsou znázorněny na obrázku níže. Tato rovnovážná poloha je tedy stabilní.
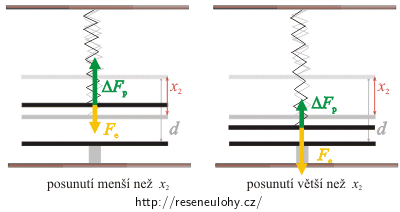
Nyní se podíváme na druhý průsečík zelené křivky s přímkou. V tomto případě se deska ustálí ve vzdálenosti x2. Jestliže toto posunutí zmenšíme, bude síla pružnosti větší než síla elektrická. Deska se tedy do rovnovážné polohy nevrátí. Pokud posunutí zvětšíme, bude elektrická síla větší než síla pružiny. Deska se opět do rovnovážné polohy nevrátí. Viz obrázek níže. Tato rovnovážná poloha je labilní.
Hranicí mezi labilní a stabilní rovnováhou je stav, kdy je na kondenzátoru maximální napětí. V grafu je velikost elektrické síly v závislosti na poloze horní desky při tomto napětí zakreslena červeně. V tomto případě existuje pouze jedna vzdálenost, pro kterou jsou desky v rovnováze. V ostatních případech je vždy elektrická síla větší než síla pružnosti a horní deska bude přitažena až dolů k druhé desce.
V praxi to tedy bude vypadat tak, že při zvětšování napětí bude horní deska postupně klesat a desky budou ve stabilní rovnováze. Poté, co napětí dosáhne maximální hodnoty, bude elektrická síla větší než síla pružnosti pro jakoukoli polohu desky a desky se samovolně spojí.
d) Nápověda
Hranicí mezi stabilní a labilní rovnováhou je poloha desky, kdy má napětí nejvyšší hodnotu a desky jsou v rovnováze.
Extrém funkce (minimum nebo maximum) se nachází ve stacionárních bodech nebo v bodech, kde neexistuje první derivace. Stacionární body najdeme tak, že derivaci funkce položíme rovnou nule \(\frac{\mathrm{d} f}{\mathrm{d} x} \, =\,0\).
d) Řešení: Maximální napětí pro stabilní rovnováhu
Hranicí stabilní rovnováhy je maximum křivky v grafu. Podíváme-li se na graf (nebo do tabulky hodnot) můžeme nejdříve maximum odhadnout. Maximum napětí má hodnotu asi 160 V. Napětí je maximální, když je posunutí horní desky přibližně mezi hodnotami 0,6 mm a 0,7 mm. Přesnou hodnotu napětí zjistíme, pokud spočítáme maximum funkce.
Extrém funkce (minimum nebo maximum) se nachází ve stacionárních bodech nebo v bodech, kde neexistuje první derivace. Stacionární body najdeme řešením rovnice \(\frac{\mathrm{d} f}{\mathrm{d} x} \, =\,0\).
Nejdříve vztah pro napětí upravíme, aby se lépe derivoval. Konstanty si vytkneme zvlášť dopředu a částečně odmocníme:
\[ \frac{\mathrm{d}U}{\mathrm{d}x}\,=\,\frac{\mathrm{d}}{\mathrm{d}x} \sqrt{\frac{2kx\left(d-x\right)^2}{\varepsilon_0 S }}\,=\,\frac{\mathrm{d}}{\mathrm{d}x} \sqrt{\frac{2k}{\varepsilon_0 S }}\sqrt{x}\left(d-x\right)\,.\]Konstantu \(\sqrt{\frac{2k}{\varepsilon_0 S }}\) můžeme dát před derivaci:
\[ \frac{\mathrm{d}U}{\mathrm{d}x}\,=\,\sqrt{\frac{2k}{\varepsilon_0 S }}\,\frac{\mathrm{d}}{\mathrm{d}x} \sqrt{x}\left(d-x\right)\,.\]Zderivujeme součin:
\[ \frac{\mathrm{d}U}{\mathrm{d}x}\,=\,\sqrt{\frac{2k}{\varepsilon_0 S }}\, \left(\frac{\mathrm{d}\sqrt{x}}{\mathrm{d}x} \left(d-x\right)+\sqrt{x}\frac{\mathrm{d}\left(d-x\right)}{\mathrm{d}x} \right)\,,\] \[\frac{\mathrm{d}U}{\mathrm{d}x}\,=\,\sqrt{\frac{2k}{\varepsilon_0 S }}\, \left(\frac{1}{2\sqrt{x}} \left(d-x\right)-\sqrt{x} \right)\,.\]Nyní už derivaci položíme rovnu nule:
\[ \sqrt{\frac{2k}{\varepsilon_0 S }}\, \left(\frac{1}{2\sqrt{x}} \left(d-x\right)-\sqrt{x} \right)\,=\,0.\]Zkrátíme konstantu a rovnici budeme upravovat, abychom vyjádřili posunutí x:
\[ \frac{1}{2\sqrt{x}} \left(d-x\right)-\sqrt{x}\,=\,0,\] \[ \frac{1}{2\sqrt{x}} \left(d-x\right)\,=\,\sqrt{x} \hspace{20px}|\cdot 2\sqrt{x},\] \[ d-x\,=\,2x\hspace{20px}|\cdot +x,\] \[ d\,=\,3x\hspace{20px}| \cdot \frac{1}{3},\] \[ x\,=\,\frac{d}{3}.\]Pro tuto hodnotu x je tedy napětí maximální. Jeho hodnotu spočítáme dosazením \( x\,=\,\frac{d}{3}\) do vztahu (***):
\[U\,=\,\sqrt{\frac{2kx\left(d-x\right)^2}{\varepsilon_0 S }}, \] \[U_{\mathrm{max}}\,=\,\sqrt{\frac{2k\frac{d}{3}\left(d-\frac{d}{3}\right)^2}{\varepsilon_0 S }}\,=\,\sqrt{\frac{2k\frac{d}{3}\left(\frac{2d}{3}\right)^2}{\varepsilon_0 S }}. \]Výraz částečně odmocníme:
\[U_{\mathrm{max}}\,=\,\frac{2d}{3}\sqrt{\frac{2k\frac{d}{3}}{\varepsilon_0 S }}\,=\,\frac{2d}{3}\sqrt{\frac{2kd}{3\varepsilon_0 S }}. \]Získali jsme výsledný vztah pro výpočet maximálního napětí, tedy největší napětí, při kterém jsou desky ještě ve stabilní rovnováze:
\[U_{\mathrm{max}}\,=\,\frac{2d}{3}\sqrt{\frac{2kd}{3\varepsilon_0 S }}. \]d) Zápis a číselný výpočet maximálního napětí
\[S\,=\,100\,\mathrm{cm^2}\,=\,0{,}01\,\mathrm{m^2}\] \[k\,=\,1\,\mathrm{Nm^{-1}}\] \[d\,=\,2\,\mathrm{mm}\,=\,2{\cdot}10^{-3}\,\mathrm{m}\]Konstanty vyhledané v tabulkách:
\[\varepsilon_0\,=\,8{,}85{\cdot} 10^{-12}\,\mathrm{ C^2\,N^{-1}\,m^{-2}}\]
\[x_{\mathrm{max}}\,=\,\frac{d}{3}\,=\,\frac{2{\cdot}10^{-3}}{3}\,\dot=\,6{,}7 {\cdot}10^{-4}\,\mathrm{m}\,\dot=\,0{,}67\, \mathrm{mm}\] \[U_{\mathrm{max}}\,=\,\frac{2d}{3}\sqrt{\frac{2kd}{3\varepsilon_0 S }} \,=\,\frac{2{\cdot} 2\cdot10^{-3}}{3}\sqrt{\frac{2 {\cdot} 2\cdot 10^{-3}}{3{\cdot} 8{,}85 {\cdot} 10^{-12} \cdot 0{,}01}}\] \[U_{\mathrm{max}}\, \dot= \, 164\, \mathrm{V}\]Odpověď
a) Napětí závisí na posunutí podle vztahu \(U\,=\,\sqrt{\frac{2kx\left(d-x\right)^2}{\varepsilon_0 S }}\).
b)
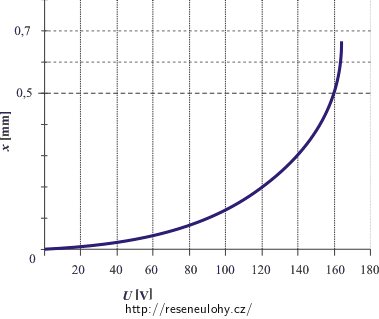
c) Pro malá napětí se desky nacházejí ve stabilní rovnováze, poloha horní desky postupně roste s rostoucím napětím. Kromě této stabilní rovnovážné polohy existuje pro dané napětí ještě jedna rovnovážná poloha odpovídající větší výchylce horní desky, ale tato poloha je labilní. Poté, co napětí dosáhne maximální hodnoty, desky se samovolně spojí, protože pro napětí větší, než je hodnota maximálního napětí, neexistuje žádná rovnovážná poloha desky. Tato rovnovážná poloha neexistuje proto, že elektrická síla je pro všechny polohy horní desky větší než přírůstek síly pružiny.
d) Hranice pro existenci stabilní rovnováhy je
\[U_{\mathrm{max}}\,=\,\frac{2d}{3}\sqrt{\frac{2kd}{3\varepsilon_0 S }}\, \dot{=} \, 164\, \mathrm{V},\] \[x_{\mathrm{max}}\,=\,\frac{d}{3}\,\dot=\,0{,}67\, \mathrm{mm}.\]Vzorce pro derivace
Zde jsou uvedeny vzorce pro derivace, které jsou použity v řešení části d):
\[\frac {\mathrm{d} \left(c \cdot f\right)}{\mathrm{d}x} \,=\, c \cdot \frac {\mathrm{d}f}{\mathrm{d}x},\] \[\frac {\mathrm{d} \sqrt{x}}{\mathrm{d}x} \,=\, \frac {1}{2\sqrt{x}},\] \[\frac {\mathrm{d} \left(c - x\right)}{\mathrm{d}x} \,=\,-1\,,\]kde c je konstanta a f je libovolná funkce.
Derivace součinu
\[\frac {\mathrm{d} \left( f \cdot g \right)}{\mathrm{d}x} \,=\, \frac {\mathrm{d} f }{\mathrm{d}x}\cdot g \,+\,f \cdot\frac {\mathrm{d} g }{\mathrm{d}x},\]kde f a g jsou libovolné funkce.