Sbírka řešených úloh

Objemová hustota energie el. a mag. pole

Úloha číslo: 1404

• Vztahy užitečné pro výpočet

  Objemová hustota energie elektrického pole je dána vztahem

  \[w_\mathrm{E} = \frac{1}{2} \vec{E} \cdot \vec{D}.\]

  Objemová hustota energie magnetického pole je dána vztahem

  \[w_\mathrm{M} = \frac{1}{2} \vec{H} \cdot \vec{B}.\]

  Velikost časové střední hodnoty Poyntingova vektoru je pro rovinnou vlnu ve vakuu (vypočítáno zde)

  \[ \|\langle \vec{S} \rangle \| = \|\langle\vec{E} \times \vec{H} \rangle \|= \frac{1}{2z_0} E_0^2. \]

  Ve vakuu souvisí vektory indukcí a intenzit vztahy

  \[ \begin{eqnarray} \vec{B} &=& \mu_0 \vec{H}, \\ \vec{D} &=& \varepsilon_0 \vec{E}. \end{eqnarray} \]

  Vztah mezi velikostmi amplitud rovinné vlny ve vakuu

  \[E_0 = cB_0.\]

  Časová střední hodnota funkce \(\cos^2 (at + b)\) přes periodu \(T\) je

  \[\langle \cos^2 (at + b) \rangle = \frac{1}{2},\]

  Odvození

  \[\frac{1}{T}\int_0^{T} \underbrace{\cos^2 (at+b)}_{\frac{1}{2}[(1+\cos (2(at+b))]}\,\mathrm{d}t = \frac{1}{2T}\int_0^{T}\left[t +\frac{\sin (2at+2b)}{2a}\right]_0^{T} = \frac{1}{2}.\]

  Rychlost světla ve vakuu

  \[c = \frac{1}{\sqrt{\varepsilon_0 \mu_0}}.\]

  Charakteristická impedance vakua

  \[z_0=\sqrt\frac{\mu_0}{\varepsilon_0}.\]

• 1. Nápověda – výpočet w_E, <w_E>

  Určete objemovou hustotu energie elektrického pole vlny a její časovou střední hodnotu.

  Dosaďte do definičního vztahu

  \[w_\mathrm{E} = \frac{1}{2} \vec{E} \cdot \vec{D}\]

  s pomocí vztahu

  \[\vec{D} = \varepsilon_0 \vec{E}\]

  zadanou elektrickou intenzitu. Výraz upravte a určete časovou střední hodnotu \(\langle w_\mathrm{E} \rangle\).

• 1. Řešení nápovědy – výpočet w_E, <w_E>

  Objemová hustota energie elektrického pole je

  \[w_\mathrm{E} = \frac{1}{2} \vec{E} \cdot \vec{D} =\frac{1}{2}\varepsilon_0 \vec{E} \cdot \vec{E} = \frac{1}{2}\varepsilon_0 E^2 = \frac{1}{2}\varepsilon_0 E_0^2 \cos^2\left(\omega t - \vec{k}\cdot \vec{r} + \varphi_0\right).\]

  Vystředováním přes periodu dostáváme

  \[\langle w_\mathrm{E} \rangle = \frac{1}{2}\varepsilon_0 E_0^2 \underbrace{\left\langle \cos^2\left(\omega t - \vec{k}\cdot \vec{r} + \varphi_0\right)\right\rangle}_{\frac{1}{2}} = \frac{1}{4}\varepsilon_0 E_0^2.\]

• 2. Nápověda – výpočet w_M, <w_M>

  Určete objemovou hustotu energie magnetického pole vlny a její časovou střední hodnotu.

  Dosaďte do definičního vztahu

  \[w_\mathrm{M} = \frac{1}{2} \vec{H} \cdot \vec{B}\]

  s pomocí vztahu

  \[\vec{B} = \varepsilon_0 \vec{H}\]

  zadanou magnetickou indukci. Výraz upravte a určete časovou střední hodnotu \(\langle w_\mathrm{M} \rangle\).

• 2. Řešení nápovědy – výpočet w_M, <w_M>

  Objemová hustota energie magnetického pole je

  \[w_\mathrm{M} = \frac{1}{2} \vec{H} \cdot \vec{B} = \frac{1}{2}\frac{1}{\mu_0} \vec{B} \cdot \vec{B} = \frac{1}{2}\frac{B^2}{\mu_0} = \frac{1}{2}\frac{B_0^2}{\mu_0} \cos^2\left(\omega t - \vec{k}\cdot \vec{r} + \varphi_0\right) .\]

  Vystředováním přes periodu dostáváme

  \[\langle w_\mathrm{M} \rangle = \frac{1}{2}\frac{B_0^2}{\mu_0} \underbrace{\left\langle \cos^2\left(\omega t - \vec{k}\cdot \vec{r} + \varphi_0\right)\right\rangle}_{\frac{1}{2}} = \frac{1}{4}\frac{B_0^2}{\mu_0} .\]

• 3. Nápověda – poměr hodnot <w_E> a <w_M>

  Výsledek střední hodnoty \(\langle w_\mathrm{M}\rangle\) upravte pomocí vztahů

  \[E_0 = cB_0, \qquad c = \frac{1}{\sqrt{\varepsilon_0 \mu_0}}\]

  tak, aby byly obě střední hodnoty \(\langle w_\mathrm{E}\rangle\) a \(\langle w_\mathrm{M}\rangle\) vyjádřeny v týchž proměnných.

  Určete poměr středních hodnot objemových hustot energií, které připadají magnetickému a elektrickému poli vlny.

• 3. Řešení nápovědy – poměr hodnot <w_E> a <w_M>

  Se střední hodnotou hustoty energie elektrického pole již nic dělat nebudeme

  \[\langle w_\mathrm{E} \rangle = \frac{1}{4}\varepsilon_0 E_0^2 .\]

  Střední hodnotu hustoty energie magnetického pole upravíme tak, aby byla vyjádřena pomocí amplitudy elektrické energie

  \[\langle w_\mathrm{M} \rangle = \frac{1}{4}\frac{B_0^2}{\mu_0} = \frac{1}{4}\frac{E_0^2}{c^2 \mu_0} = \frac{1}{4}\frac{E_0^2 \mu_0 \varepsilon_0}{\mu_0} = \frac{1}{4}\varepsilon_0 E_0^2. \]

  Nyní již vidíme, že poměr

  \[ \frac{\langle w_\mathrm{E} \rangle}{\langle w_\mathrm{M} \rangle} = 1. \]

  Zatímco velikost amplitudy elektrické intenzity je \(c\)-násobná oproti amplitudě intenzity magnetické, energie je mezi elektrickou a magnetickou část rozdělena rovným dílem.

• 4. Nápověda – rychlost šíření v energie

  Určete rychlost šíření \(v\) energie.

  • Velikost časové střední hodnoty Poyntingova vektoru nám říká, kolik energie (středně) prochází kolmo jednotkovou plochou za jednotku času.

  • Součet středních hodnot hustot energií elektrického a magnetického pole nám dává střední hodnotu celkové energie (elektromagnetického pole) v jednotkovém objemu.

  • Velikost časové střední hodnoty Poyntingova vektoru rovinné vlny je

  \[ \|\langle \vec{S} \rangle \| = \frac{1}{2z_0} E_0^2 \]

  kde \(z_0\) je charakteristická impedance vakua

  \[z_0 = \sqrt\frac{\mu_0}{\varepsilon_0}.\]

  • Hustotu energie elektrického a magnetického pole souhrnně dostaneme součtem výsledků z částí 1 a 2.

• 4. Řešení nápovědy – rychlost šíření v energie

  Plochou o obsahu \(A\) za čas \(\Delta t\) kolmo projde střední energie

  \[W = \|\langle \vec{S} \rangle \| A \Delta t.\tag{1}\]

  Tato energie přísluší objemu \(Ad\), kde \(d\) je vzdálenost, mezi myšleným průřezem obsahu \(A\) a místem, kam se stihne energie za čas \(\Delta t\) rozšířit.

  

  Střední hodnota energie v objemu \(Ad\) je

  \[W = \left(\langle w_\mathrm{E} \rangle + \langle w_\mathrm{M} \rangle \right) Ad.\tag{2}\]

  Porovnáme rovnice (1) a (2)

  \[ \left(\langle w_\mathrm{E} \rangle + \langle w_\mathrm{M} \rangle \right) Ad = \|\langle \vec{S} \rangle \| A \Delta t. \]

  Vyjádříme podíl \(\frac{d}{\Delta t}\) představující velikost rychlosti šíření energie \(v\)

  \[ v = \frac{d}{\Delta t} = \frac{\|\langle \vec{S} \rangle \|} {\langle w_\mathrm{E} \rangle + \langle w_\mathrm{M} \rangle}. \]

  Dosadíme velikost střední hodnoty Poyntingova vektoru (viz teorie) a vypočítané střední hodnoty hustot energie elektrického a magnetického pole

  \[ v = \frac{\|\langle \vec{S} \rangle \|} {\langle w_\mathrm{E} \rangle + \langle w_\mathrm{M} \rangle} = \frac{\frac{1}{2z_0} E_0^2}{\frac{1}{4} \varepsilon_0 E_0^2+\frac{1}{4} \varepsilon_0 E_0^2} = \frac{\frac{1}{2} \sqrt{\frac{\varepsilon_0}{\mu_0}}E_0^2}{\frac{1}{2} \varepsilon_0 E_0^2}= \frac{1}{\sqrt{\varepsilon_0 \mu_0}}c. \]

  Rychlost šíření vlny a rychlost přenosu energie je ve vakuu stejná.

• CELKOVÉ ŘEŠENÍ

  1. Objemová hustota energie elektrického pole je

  \[w_\mathrm{E} = \frac{1}{2} \vec{E} \cdot \vec{D} =\frac{1}{2}\varepsilon_0 \vec{E} \cdot \vec{E} = \frac{1}{2}\varepsilon_0 E^2 = \frac{1}{2}\varepsilon_0 E_0^2 \cos^2\left(\omega t - \vec{k}\cdot \vec{r} + \varphi_0\right).\]

  Vystředováním přes periodu dostáváme

  \[\langle w_\mathrm{E} \rangle = \frac{1}{2}\varepsilon_0 E_0^2 \underbrace{\left\langle \cos^2\left(\omega t - \vec{k}\cdot \vec{r} + \varphi_0\right)\right\rangle}_{\frac{1}{2}} = \frac{1}{4}\varepsilon_0 E_0^2.\]

  ---

  2. Se střední hodnotou hustoty energie elektrického pole již nic dělat nebudeme

  \[\langle w_\mathrm{E} \rangle = \frac{1}{4}\varepsilon_0 E_0^2 .\]

  Střední hodnotu hustoty energie magnetického pole upravíme tak, aby byla vyjádřena pomocí amplitudy elektrické energie

  \[\langle w_\mathrm{M} \rangle = \frac{1}{4}\frac{B_0^2}{\mu_0} = \frac{1}{4}\frac{E_0^2}{c^2 \mu_0} = \frac{1}{4}\frac{E_0^2 \mu_0 \varepsilon_0}{\mu_0} = \frac{1}{4}\varepsilon_0 E_0^2. \]

  Nyní již vidíme, že poměr

  \[ \frac{\langle w_\mathrm{E} \rangle}{\langle w_\mathrm{M} \rangle} = 1. \]

  Zatímco velikost amplitudy elektrické intenzity je \(c\)-násobná oproti amplitudě intenzity magnetické, energie je mezi elektrickou a magnetickou část rozdělena rovným dílem.

  ---

  3. Se střední hodnotou hustoty energie elektrického pole již nic dělat nebudeme

  \[\langle w_\mathrm{E} \rangle = \frac{1}{4}\varepsilon_0 E_0^2 .\]

  Střední hodnotu hustoty energie magnetického pole upravíme tak, aby byla vyjádřena pomocí amplitudy elektrické energie

  \[\langle w_\mathrm{M} \rangle = \frac{1}{4}\frac{B_0^2}{\mu_0} = \frac{1}{4}\frac{E_0^2}{c^2 \mu_0} = \frac{1}{4}\frac{E_0^2 \mu_0 \varepsilon_0}{\mu_0} = \frac{1}{4}\varepsilon_0 E_0^2. \]

  Nyní již vidíme, že poměr

  \[ \frac{\langle w_\mathrm{E} \rangle}{\langle w_\mathrm{M} \rangle} = 1. \]

  Zatímco velikost amplitudy elektrické intenzity je \(c\)-násobná oproti amplitudě intenzity magnetické, energie je mezi elektrickou a magnetickou část rozdělena rovným dílem.

  ---

  4. Plochou o obsahu \(A\) za čas \(\Delta t\) kolmo projde střední energie

  \[W = \|\langle \vec{S} \rangle \| A \Delta t.\tag{1}\]

  Tato energie přísluší objemu \(Ad\), kde \(d\) je vzdálenost, mezi myšleným průřezem obsahu \(A\) a místem, kam se stihne energie za čas \(\Delta t\) rozšířit.

  

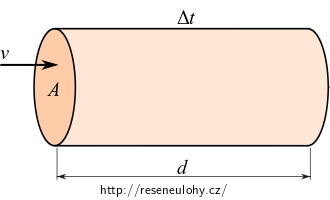
  Střední hodnota energie v objemu \(Ad\) je

  \[W = \left(\langle w_\mathrm{E} \rangle + \langle w_\mathrm{M} \rangle \right) Ad.\tag{2}\]

  Porovnáme rovnice 1 a 2

  \[ \left(\langle w_\mathrm{E} \rangle + \langle w_\mathrm{M} \rangle \right) Ad = \|\langle \vec{S} \rangle \| A \Delta t. \]

  Vyjádříme podíl \(\frac{d}{\Delta t}\) představující velikost rychlosti šíření energie \(v\)

  \[ v = \frac{d}{\Delta t} = \frac{\|\langle \vec{S} \rangle \|} {\langle w_\mathrm{E} \rangle + \langle w_\mathrm{M} \rangle}. \]

  Dosadíme velikost střední hodnoty Poyntingova vektoru (viz teorie) a vypočítané střední hodnoty hustot energie elektrického a magnetického pole

  \[ v = \frac{\|\langle \vec{S} \rangle \|} {\langle w_\mathrm{E} \rangle + \langle w_\mathrm{M} \rangle} = \frac{\frac{1}{2z_0} E_0^2}{\frac{1}{4} \varepsilon_0 E_0^2+\frac{1}{4} \varepsilon_0 E_0^2} = \frac{\frac{1}{2} \sqrt{\frac{\varepsilon_0}{\mu_0}}E_0^2}{\frac{1}{2} \varepsilon_0 E_0^2}= \frac{1}{\sqrt{\varepsilon_0 \mu_0}}c. \]

  Rychlost šíření vlny a rychlost přenosu energie je ve vakuu stejná.

• Odpověď

  Pro rovinnou harmonickou vlnu ve vakuu jsme určili:

  1. Prostorovou hustotu energie elektrického pole \[ w_\mathrm{E} = \frac{1}{2}\varepsilon_0 E_0^2 \cos^2\left(\omega t - \vec{k}\cdot \vec{r} + \varphi_0\right), \] a její časovou střední hodnotu \[ \langle w_\mathrm{E} \rangle = \frac{1}{4}\varepsilon_0 E_0^2 . \]

  2. Prostorovou hustotu energie magnetického pole \[w_\mathrm{M} = \frac{1}{2}\frac{B_0^2}{\mu_0} \cos^2\left(\omega t - \vec{k}\cdot \vec{r} + \varphi_0\right), \] a její časovou střední hodnotu po úpravě opět \[ \langle w_\mathrm{M} \rangle = \frac{1}{4}\varepsilon_0 E_0^2. \]

  3. Poměr hodnot \(\langle w_\mathrm{E} \rangle\) a \(\langle w_\mathrm{M} \rangle\) \[\frac{\langle w_\mathrm{E} \rangle}{\langle w_\mathrm{M} \rangle} = 1.\]

  4. Rychlost šíření energie

  \[v=c.\]