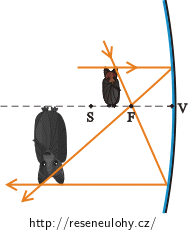
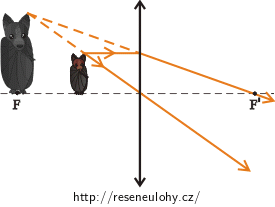
Zobrazení netopýra kulovým zrcadlem a spojnou čočkou
Úloha číslo: 1247

Mládě netopýra je \(4 \mathrm{cm}\) vysoké. Určete
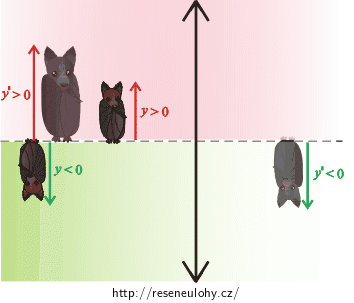
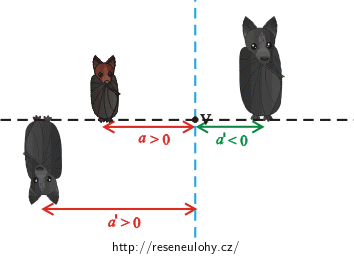
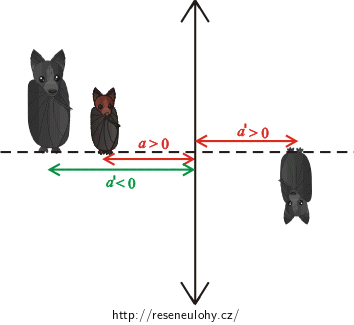
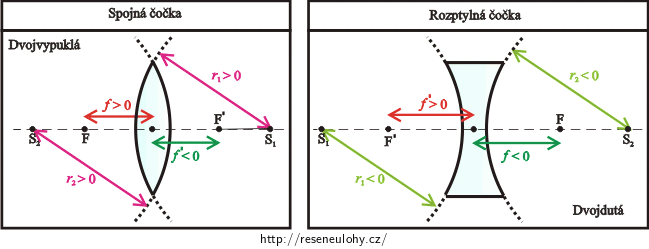
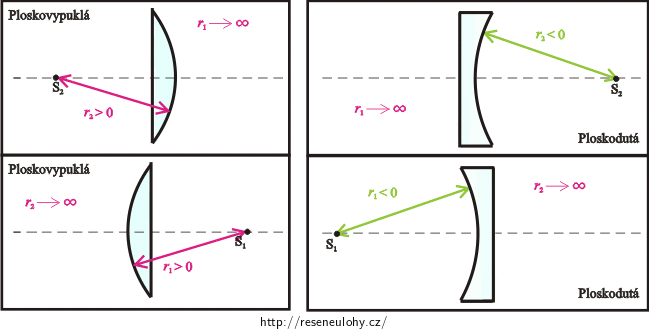
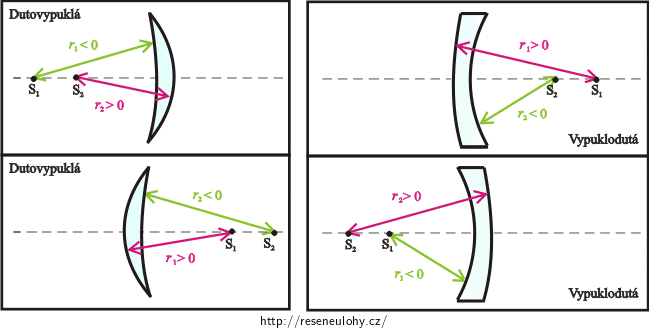
Znaménková konvence pro kulová zrcadla a pro čočky
V dalším výkladu budeme předpokládat, že se paprsky světla vždy šíří zleva doprava.
Poznámka: Znaménkovou konvenci jsme zvolili tak, jak je uvedena v učebnici pro gymnázia. Můžete se setkat i s jinak zvolenou znaménkovou konvencí, která však vede k modifikaci vztahů geometrické optiky. Vždy je proto nutné přebírat vztahy i s jejich znaménkovou konvencí.
Nápověda 1
Využijte znaménkové konvence a napište zápis úlohy.
Nápověda 2
V obou případech (a) i b)) máme zadanou výšku předmětu \(y \), výšku obrazu \(y'\) a obrazovou vzdálenost \(a'\). Potřebujeme najít vztah mezi těmito veličinami. Čemu odpovídá poměr výšky obrazu a výšky předmětu?
Nápověda 3
Uvědomte si, že tvar zobrazovací rovnice je stejný jak pro kulová zrcadla, tak pro čočky. Využitím zobrazovací rovnice a vztahu (3) z předchozí nápovědy určete ohniskovou vzdálenost \(f\).
Nápověda 4
Nyní již můžeme vypočítat ohniskovou vzdálenost spojné čočky. Ještě ale potřebujeme zjistit, jaký je vztah mezi ohniskovou vzdáleností kulového zrcadla \(f\) a jeho poloměrem křivosti \(r\). Využitím vztahu (4) vyjádřete poloměr křivosti \(r\).
Nápověda 5
Celkové řešení
Zápis
\(y= 4 \mathrm{cm}\) výška mláděte netopýra a) Zobrazení kulovým zrcadem \(y'=−8 \mathrm{cm}\) výška obrazu mláděte netopýra (*) \(a'= 12 \mathrm{cm}\) obrazová vzdálenost (**) \(r= ?\) poloměr křivosti zrcadla (?) (*) Dle zadání je výška obrazu dvojnásobná oproti výšce předmětu (\(2{\cdot}4 \mathrm{cm}= 8 \mathrm{cm}\)). Hodnota výšky obrazu je záporná, protože je obraz převrácený a nachází se tedy pod optickou osou.
(**) Obrazová vzdálenost je kladná, protože se obraz nachází před zrcadlem.
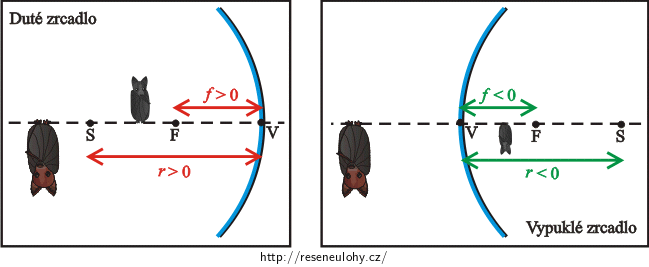
(?) Dle znaménkové konvence poloměr křivosti bude kladný, pokud se jedná o duté zrcadlo a záporný pro vypuklé zrcadlo.
b) Zobrazení spojnou čočkou \(y'= 8 \mathrm{cm}\) výška obrazu mláděte netopýra (***) \(a'=−12 \mathrm{cm}\) obrazová vzdálenost (****) \(f= ?\) ohnisková vzdálenost spojné čočky (??) (***) Dle zadání je výška obrazu dvojnásobná oproti výšce předmětu (\(2{\cdot}4 \mathrm{cm}= 8 \mathrm{cm}\)). Hodnota výšky obrazu je kladná, protože je obraz přímý a nachází se tedy nad optickou osou.
(****) Obrazová vzdálenost je záporná, protože se obraz nachází před čočkou.
(??) Dle znaménkové konvence je ohnisková vzdálenost spojné čočky kladná.
Poměr výšky obrazu a předmětu
Potřebujeme najít vztah mezi předmětovou vzdáleností \(a\), obrazovou vzdáleností \(a'\), výškou předmětu \(y\) a výškou obrazu \(y'\). Poměr výšky obrazu a výšky předmětu odpovídá příčnému zvětšení \(Z\): \[ Z=\frac{y'}{y}.\tag{1}\]
Dále pro příčné zvětšení \(Z\) platí: \[ Z=−\frac{a'}{a},\tag{2}\] kde \(a\) je předmětová vzdálenost a \(a'\) je obrazová vzdálenost.
Porovnáním (1), (2) dostaneme vztah mezi \(y \), \(y'\) a \(a'\): \[ \frac{y'}{y}=−\frac{a'}{a}.\tag{3}\] Nyní jsme si připravili vztah, který použijeme dále v řešení.
Zobrazovací rovnice
Uvědomíme si, že tvar zobrazovací rovnice je stejný jak pro kulová zrcadla, tak pro čočky: \[\frac{1}{a}+\frac{1}{a'}=\frac{1}{f}.\] Chceme vyjádřit ohniskovou vzdálenost \(f\). Nejprve převedeme zlomky na levé straně rovnice na společného jmenovatele: \[\frac{a'+a}{a\cdot a'}=\frac{1}{f}.\] Tedy: \[f=\frac{a\cdot a'}{a'+a}.\] V čitateli i ve jmenovateli vytkneme \(a\): \[f=\frac{a\cdot a'}{a\left(\frac{a'}{a}+1\right)},\] \[f=\frac{a'}{\frac{a'}{a}+1}.\] Dosadíme za zlomek \(\frac{a'}{a}\) dle vztahu (3): \[f=\frac{a'}{\left(−\frac{y'}{y}\right)+1}.\] Upravujeme výraz: \[f=\frac{a'}{\frac{−y'+y}{y}},\] \[f=\frac{a'\cdot y}{y−y'}.\tag{4}\] Získali jsme rovnici pro výpočet ohniskové vzdálenosti čočky. U kulového zrcadla nehledáme ohniskovou vzdálenost, ale poloměr křivosti. Proto v následující části vyjádříme vztah pro poloměr křivosti zrcadla.
Poloměr křivosti
Poloměr křivosti kulového zrcadla odpovídá dvojnásobku jeho ohniskové vzdálenosti: \[r= 2f.\] Dosadíme za \(f\) dle (4): \[r= 2\frac{a'\cdot y}{y−y'}.\tag{5}\]
Číselné řešení
a) Hledání poloměru křivosti kulového zrcadlaZe zadání a užitím znaménkové konvence:
\(y= 4 \mathrm{cm}\)
\(y'=−8 \mathrm{cm}\)
\(a'= 12 \mathrm{cm}\)
Dosadíme hodnoty do vztahu (5):
\(r= 2\frac{a'\cdot y}{y−y'}= 2\cdot \frac{12{\cdot} 4}{4−\left(−8\right)} \mathrm{cm}= 2\cdot \frac{48}{12} \mathrm{cm}= 8 \mathrm{cm}.\)
Jedná se o duté zrcadlo, protože poloměr křivosti má kladnou hodnotu.
b) Hledání ohniskové vzdálenosti spojné čočkyZe zadání a užitím znaménkové konvence:
\(y= 4 \mathrm{cm}\)
\(y'= 8 \mathrm{cm}\)
\(a'=−12 \mathrm{cm}\)
Dosadíme hodnoty do vztahu (4):
\(f=\frac{a'\cdot y}{y−y'}= \frac{−12{\cdot} 4}{4−8} \mathrm{cm}=\frac{−48}{−4} \mathrm{cm}= 12 \mathrm{cm}.\)
Ohnisková vzdálenost má kladnou hodnotu, jak jsme u spojné čočky předpokládali.
Odpověď
a) Poloměr křivosti kulového zrcadla je \( 8 \mathrm{cm}\). Jedná se o duté zrcadlo.
b) Ohnisková vzdálenost spojné čočky je \( 12 \mathrm{cm}\).
Jak daleko před čočkou či zrcadlem se netopýr nachází?
Hledáme předmětovou vzdálenost \(a\). V obou případech využijeme vztah: \[ \frac{y'}{y}=−\frac{a'}{a}.\tag{3}\] Vyjádříme předmětovou vzdálenost: \[ a=−\frac{y}{y'}a'.\]
Kulové zrcadlo
\(y= 4 \mathrm{cm}\)
\(y'=−8 \mathrm{cm}\)
\(a'= 12 \mathrm{cm}\)
Dosadíme:
\( a=−\frac{y}{y'}a'=−\frac{4}{\left(−8\right)}\cdot 12 \mathrm{cm}=6 \mathrm{cm}.\)
Spojná čočka
\(y= 4 \mathrm{cm}\)
\(y'= 8 \mathrm{cm}\)
\(a'=−12 \mathrm{cm}\)
Dosadíme:
\( a=−\frac{y}{y'}a'=−\frac{4}{8}\cdot \left(−12\right) \mathrm{cm}=6 \mathrm{cm}.\)
Vidíme, že netopýr se nachází \(6 \mathrm{cm}\) před kulovým zrcadlem či čočkou.